Cómo hacer un Histograma y Polígono de Frecuencias
¡Hola, amigos de Fisimat! 🚀 Si alguna vez te has sentido abrumado por una larga lista de números y has deseado tener una forma de "ver" lo que realmente significan, estás en el lugar correcto. En el vasto universo de la probabilidad y la estadística, existen herramientas increíblemente poderosas que transforman el caos de los datos en conocimiento claro y visual. Dos de las herramientas más fundamentales y utilizadas son el histograma y el polígono de frecuencias.
Entender cómo construir e interpretar estos gráficos no es solo una habilidad académica; es una competencia esencial en campos que van desde la ingeniería y la física hasta la economía y las ciencias sociales. Te permiten descubrir patrones, entender la distribución de tus datos y comunicar tus hallazgos de una manera que todos pueden entender. En este artículo, te guiaremos paso a paso, con ejemplos claros y explicaciones profundas, para que domines el arte de crear histogramas y polígonos de frecuencia como un verdadero profesional. ¡Vamos a empezar a darle forma a esos datos! 📊
- ¿Qué es un Histograma y por qué es tan importante?
- Paso a Paso: Cómo Construir un Histograma Desde Cero
- Del Histograma al Polígono de Frecuencias: Un Salto Visual
- Cómo Construir un Polígono de Frecuencias
- Interpretando las Formas: ¿Qué Nos Dicen Nuestros Gráficos? 🧐
- Conclusión: El Poder de la Visualización de Datos
¿Qué es un Histograma y por qué es tan importante?
Imagina que has medido la altura de 100 estudiantes en una universidad. Tienes una lista de 100 números. ¿Cómo puedes entender rápidamente cómo se distribuyen estas alturas? ¿La mayoría de los estudiantes son de estatura media, o hay muchos estudiantes muy altos y muchos muy bajos? Aquí es donde el histograma entra en escena como un superhéroe visual.
Histograma
Un histograma es una representación gráfica de la distribución de un conjunto de datos numéricos y continuos. Consiste en una serie de rectángulos (barras) adyacentes, donde el ancho de cada rectángulo representa un intervalo de clase y la altura representa la frecuencia (el número de datos que caen en ese intervalo).
A primera vista, un histograma puede parecer un simple gráfico de barras, pero hay una diferencia crucial: un histograma representa datos continuos agrupados en intervalos, mientras que un gráfico de barras representa datos discretos o categóricos. En un histograma, las barras se tocan entre sí para mostrar que la variable en el eje horizontal es continua. Su principal objetivo es mostrar la forma de la distribución de los datos, permitiéndonos identificar características como la tendencia central, la dispersión y la simetría.
El desarrollo de estas técnicas visuales fue un gran paso para la estadística moderna, y debemos mucho de ello a pioneros en el campo.
Karl Pearson
1857-1936
Un matemático y bioestadístico inglés, es considerado uno de los fundadores de la estadística matemática. Aunque no inventó el histograma, fue él quien acuñó el término en 1891 y lo popularizó como una herramienta fundamental para el análisis de datos. Su trabajo sentó las bases para muchas de las técnicas estadísticas que utilizamos hoy en día.
La importancia del histograma radica en su capacidad para simplificar la complejidad. Con una sola mirada, podemos responder preguntas como:
- ¿Dónde se concentran la mayoría de los datos? (Tendencia central)
- ¿Qué tan dispersos están los datos? (Variabilidad)
- ¿La distribución es simétrica o está sesgada hacia un lado? (Asimetría)
- ¿Existen valores atípicos o inusuales? (Outliers)
Ahora que entendemos qué es y por qué es tan valioso, es hora de arremangarse y aprender a construir uno desde cero. 🛠️
Paso a Paso: Cómo Construir un Histograma Desde Cero
Construir un histograma es un proceso metódico. Aunque el software moderno puede hacerlo en segundos, entender el proceso manual es crucial para interpretar correctamente el resultado y tomar decisiones informadas. Vamos a desglosarlo en seis pasos sencillos.
Paso 1: Recopilar los Datos (N)
El primer paso es, por supuesto, tener un conjunto de datos. Supongamos que queremos analizar las calificaciones finales de un examen de física para una clase de 50 estudiantes. Lo primero es contar cuántos datos tenemos. A este número lo llamamos \(N\).
En nuestro caso, \(N = 50\).
Paso 2: Determinar el Rango (R)
El rango es la diferencia entre el valor máximo y el valor mínimo en nuestro conjunto de datos. Nos da una idea de la dispersión total de los datos.
Fórmula del Rango: \[R = \text{Valor Máximo} - \text{Valor Mínimo}\]
Busca en tu lista de datos el número más alto y el más bajo. Si la calificación más alta fue de 98 y la más baja fue de 53, el rango sería: \(R = 98 - 53 = 45\).
Paso 3: Decidir el Número de Clases o Intervalos (k)
Este es quizás el paso más subjetivo, pero es fundamental. El número de clases (las "barras" de nuestro histograma) determinará qué tan detallado será el gráfico. Si usamos muy pocas clases, podemos perder información importante. Si usamos demasiadas, el gráfico puede volverse ruidoso y difícil de interpretar. Afortunadamente, existen reglas que nos ayudan a elegir un buen punto de partida. La más conocida es la Regla de Sturges.
Regla de Sturges
Es una fórmula empírica que proporciona una estimación del número óptimo de clases (\(k\)) para un histograma, basado en el número total de observaciones (\(N\)).
Fórmula: \[k = 1 + 3.322 \cdot \log_{10}(N)\]
Para nuestros 50 estudiantes (\(N=50\)), aplicaríamos la fórmula así:
\(k = 1 + 3.322 \cdot \log_{10}(50) \approx 1 + 3.322 \cdot (1.6989) \approx 1 + 5.643 \approx 6.643\)
El resultado casi nunca es un número entero. Lo redondeamos al entero más cercano. En este caso, podemos elegir usar \(k=7\) clases.
Paso 4: Calcular la Amplitud de Clase (A)
La amplitud o ancho de clase es el tamaño de cada intervalo. Idealmente, todos los intervalos en un histograma deben tener el mismo ancho. Para calcularlo, simplemente dividimos el rango por el número de clases.
Fórmula de la Amplitud: \[A = \frac{R}{k}\]
Usando nuestros valores: \(A = \frac{45}{7} \approx 6.42\).
Al igual que con el número de clases, es una buena práctica redondear este número hacia arriba a un valor más conveniente y fácil de manejar, como 7 o incluso 10, dependiendo del contexto. Para nuestro ejemplo, redondear a \(A=7\) parece razonable.
Paso 5: Crear la Tabla de Frecuencias
Este es el corazón organizativo de nuestro histograma. La tabla de frecuencias nos ayudará a contar cuántos datos caen en cada clase. La tabla suele tener las siguientes columnas:
- Clase o Intervalo: Los rangos de valores para cada barra. Empezamos con el valor mínimo (o un poco menos para asegurar que entre) y le sumamos la amplitud (\(A\)) para obtener el límite superior de la primera clase. El límite inferior de la siguiente clase será el límite superior de la anterior. Por ejemplo, si empezamos en 53, con una amplitud de 7, los intervalos serían [53, 60), [60, 67), [67, 74), y así sucesivamente.
- Conteo o Tally: Una columna opcional donde puedes hacer marcas para contar los datos a medida que los revisas.
- Frecuencia Absoluta (\(f_i\)): El número total de observaciones que caen dentro de cada intervalo. La suma de todas las frecuencias debe ser igual a \(N\).
- Marca de Clase (\(x_i\)): Es el punto medio de cada intervalo. Se calcula como \((\text{Límite Inferior} + \text{Límite Superior}) / 2\). Este valor será crucial para construir el polígono de frecuencias más adelante.
Paso 6: Dibujar el Histograma
¡Es hora de visualizar! 🎨
- Dibuja los Ejes: El eje horizontal (eje X) representará los intervalos de clase. El eje vertical (eje Y) representará la frecuencia.
- Etiqueta los Ejes: Asegúrate de nombrar claramente cada eje (p. ej., "Calificaciones del Examen" para el eje X y "Número de Estudiantes" para el eje Y).
- Dibuja las Barras: Para cada clase de tu tabla de frecuencias, dibuja un rectángulo. La base del rectángulo debe cubrir el intervalo de clase en el eje X, y la altura debe corresponder a la frecuencia de esa clase en el eje Y.
- Recuerda: ¡Las barras deben estar pegadas unas a otras!
Ejemplo 1: Construyendo Nuestro Primer Histograma
Un ingeniero de calidad ha registrado el tiempo de vida (en horas) de 40 baterías de un nuevo modelo. Los datos son los siguientes: 125, 132, 128, 141, 135, 145, 120, 131, 138, 142, 148, 129, 133, 137, 139, 140, 124, 136, 134, 144, 126, 130, 147, 136, 133, 128, 141, 131, 135, 139, 146, 134, 127, 143, 138, 135, 131, 140, 132, 137. Construyamos el histograma.
Solución:
Sigamos nuestros pasos metódicamente:
Paso 1: Recopilar los Datos
Tenemos \(N = 40\) mediciones.
Paso 2: Determinar el Rango (R)
Valor Máximo = 148 horas.
Valor Mínimo = 120 horas.
Rango: \(R = 148 - 120 = 28\).
Paso 3: Decidir el Número de Clases (k)
Usando la Regla de Sturges: \(k = 1 + 3.322 \cdot \log_{10}(40) \approx 1 + 3.322 \cdot (1.602) \approx 1 + 5.32 \approx 6.32\).
Redondeamos y decidimos usar \(k=6\) clases.
Paso 4: Calcular la Amplitud de Clase (A)
\(A = \frac{R}{k} = \frac{28}{6} \approx 4.67\).
Para facilitar el trabajo, redondeamos la amplitud hacia arriba a un número entero conveniente. Usemos \(A=5\).
Paso 5: Crear la Tabla de Frecuencias
Comenzaremos nuestro primer intervalo un poco antes del mínimo para asegurarnos de que entre bien, por ejemplo en 120.
| Intervalo de Clase (horas) | Frecuencia (\(f_i\)) | Marca de Clase (\(x_i\)) |
|---|---|---|
| [120 - 125) | 3 | 122.5 |
| [125 - 130) | 6 | 127.5 |
| [130 - 135) | 9 | 132.5 |
| [135 - 140) | 10 | 137.5 |
| [140 - 145) | 7 | 142.5 |
| [145 - 150) | 5 | 147.5 |
| Total | 40 | - |
Paso 6: Dibujar el Histograma
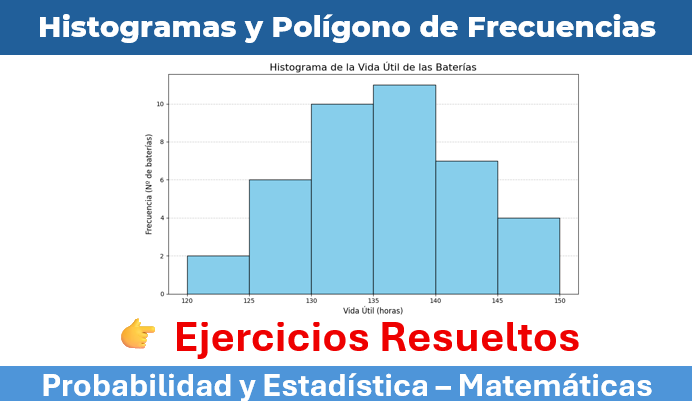
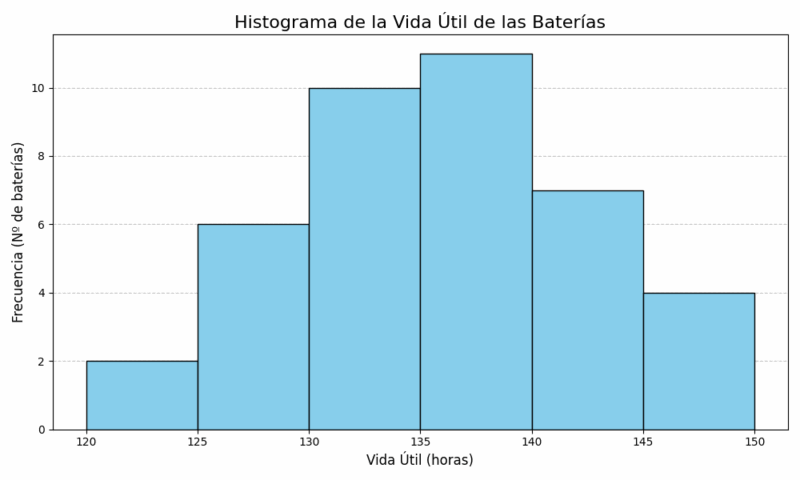
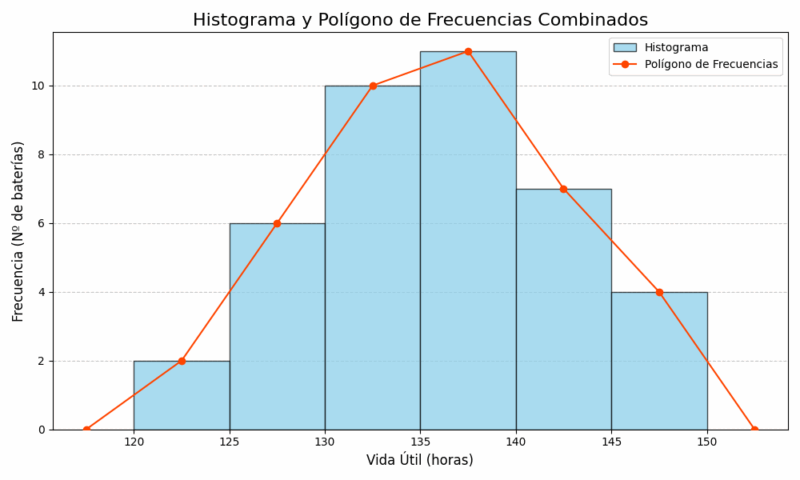
Ahora, dibujaríamos un gráfico con el eje X mostrando los intervalos [120-125), [125-130), etc., y el eje Y mostrando las frecuencias (de 0 a 10). Dibujaríamos 6 barras adyacentes con alturas de 3, 6, 9, 10, 7 y 5 respectivamente.
En este ejemplo hicimos el mismo ejercicio con Python para graficar nuestro histograma, aunque parece que estuviera diferente al que hemos hecho, debemos entender que a nivel computación sé es más estricto la forma de tomar los valores y por eso puede variar pero no está mal en absoluto.
Del Histograma al Polígono de Frecuencias: Un Salto Visual
Una vez que tenemos nuestro histograma, crear un polígono de frecuencias es un paso muy natural. De hecho, es una forma alternativa y a veces más clara de representar la misma información.
Polígono de Frecuencias
Un polígono de frecuencias es un gráfico de líneas que se construye uniendo los puntos medios (marcas de clase) de la parte superior de cada barra de un histograma. Proporciona una mejor visualización de la forma de la distribución de los datos.
¿Por qué usar un polígono de frecuencias si ya tenemos el histograma? Bueno, tiene algunas ventajas:
- Comparación Sencilla: Es mucho más fácil superponer dos o más polígonos de frecuencia en el mismo gráfico para comparar diferentes distribuciones de datos que superponer dos histogramas.
- Continuidad Visual: La línea continua del polígono a menudo da una mejor impresión de la continuidad de la distribución.
Cómo Construir un Polígono de Frecuencias
El trabajo pesado ya está hecho con la tabla de frecuencias. Ahora solo necesitamos usar las marcas de clase que calculamos.
Paso 1: Usar la Tabla de Frecuencias Existente
Necesitas la columna de Marcas de Clase (\(x_i\)) y la columna de Frecuencia (\(f_i\)).
Paso 2: Representar los Puntos en el Gráfico
Para cada clase, vas a trazar un punto. La coordenada X del punto será la marca de clase (\(x_i\)), y la coordenada Y será la frecuencia (\(f_i\)). Así que trazarás los puntos \((x_i, f_i)\).
Paso 3: Unir los Puntos y Cerrar el Polígono
Con una regla, une los puntos que trazaste en orden con segmentos de línea recta. Para "cerrar" el polígono y darle una apariencia completa, se añade una marca de clase adicional al principio y al final, ambas con frecuencia cero. Estos puntos se sitúan en el eje X, anclando el gráfico y representando que no hay datos antes del primer intervalo ni después del último.
Ejemplo 2: Trazando el Polígono de Frecuencias
Utilizando los datos y la tabla de frecuencias del Ejemplo 1 sobre la vida de las baterías, vamos a construir el polígono de frecuencias correspondiente.
Solución:
Paso 1: Usar la Tabla de Frecuencias
Ya tenemos nuestras marcas de clase y frecuencias del ejemplo anterior.
Paso 2: Identificar los Puntos a Trazar
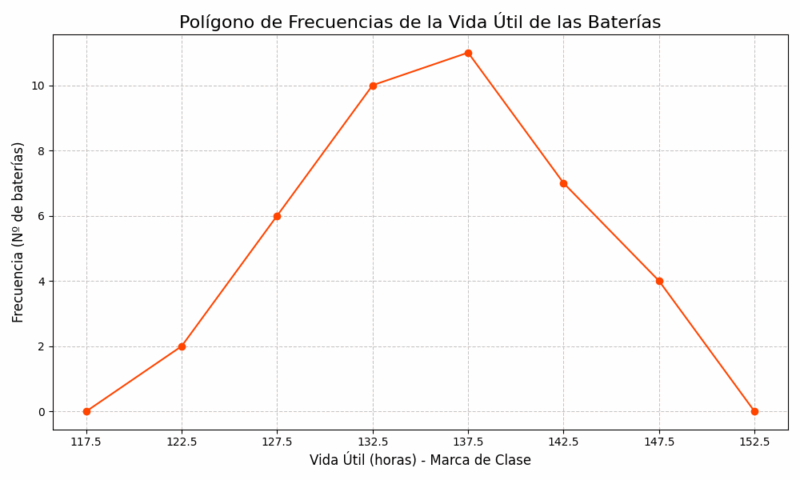
Los puntos \((x_i, f_i)\) que necesitamos trazar son:
(122.5, 3), (127.5, 6), (132.5, 9), (137.5, 10), (142.5, 7), (147.5, 5)
Paso 3: Cerrar el Polígono
Para anclar el gráfico al eje X, necesitamos dos puntos adicionales con frecuencia cero.
- Punto inicial: Calculamos la marca de clase del intervalo "anterior" al primero. Como la amplitud es 5, sería \(122.5 - 5 = 117.5\). Nuestro primer punto será (117.5, 0).
- Punto final: Calculamos la marca de clase del intervalo "siguiente" al último. Sería \(147.5 + 5 = 152.5\). Nuestro último punto será (152.5, 0).
Ahora, en nuestro sistema de coordenadas, trazamos todos estos puntos y los unimos con líneas rectas. El resultado es un polígono que muestra claramente el pico de la distribución y cómo las frecuencias aumentan y disminuyen.
Ejemplo 3: Análisis de Control de Calidad en Producción de Café
Una empresa cafetalera quiere asegurarse de que sus paquetes de 500 gramos cumplen con el peso especificado. Se toma una muestra aleatoria de 35 paquetes y se registran sus pesos exactos. Los datos (en gramos) son: 498, 501, 503, 499, 500, 505, 496, 502, 504, 497, 500, 501, 506, 498, 503, 500, 499, 502, 507, 495, 501, 500, 498, 504, 502, 499, 501, 505, 497, 503, 500, 502, 498, 504, 501. Se necesita crear un histograma y un polígono de frecuencias para analizar la distribución del peso.
Solución:
Paso 1: Número de Datos (N)
Se tiene una muestra de \(N = 35\) paquetes.
Paso 2: Rango (R)
Valor Máximo = 507 g.
Valor Mínimo = 495 g.
Rango: \(R = 507 - 495 = 12\).
Paso 3: Número de Clases (k)
Usando la Regla de Sturges: \(k = 1 + 3.322 \cdot \log_{10}(35) \approx 1 + 3.322 \cdot (1.544) \approx 1 + 5.129 \approx 6.129\).
Redondeamos y decidimos usar \(k=6\) clases.
Paso 4: Amplitud de Clase (A)
\(A = \frac{R}{k} = \frac{12}{6} = 2\).
La amplitud es un número entero perfecto, \(A=2\), lo que facilita mucho la creación de los intervalos.
Paso 5: Tabla de Frecuencias
Comenzamos en el valor mínimo, 495.
| Intervalo de Clase (gramos) | Frecuencia (\(f_i\)) | Marca de Clase (\(x_i\)) |
|---|---|---|
| [495 - 497) | 2 | 496 |
| [497 - 499) | 5 | 498 |
| [499 - 501) | 7 | 500 |
| [501 - 503) | 9 | 502 |
| [503 - 505) | 6 | 504 |
| [505 - 508) | 6 | 506.5 |
| Total | 35 | - |
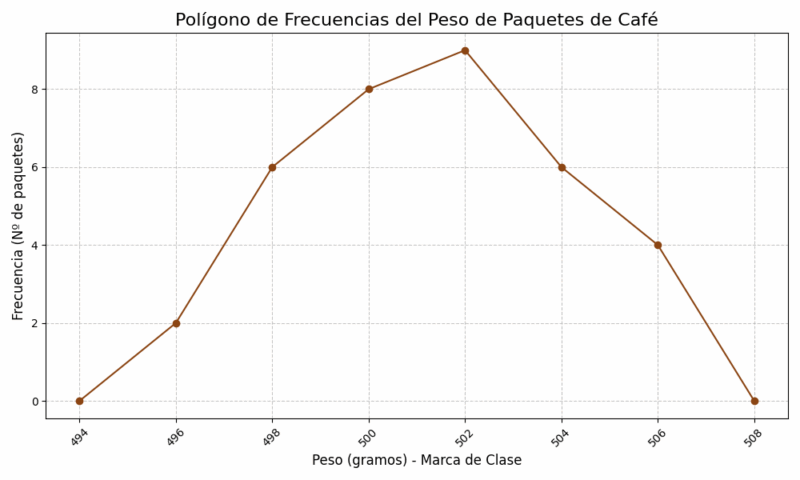
Paso 6: Dibujo e Interpretación
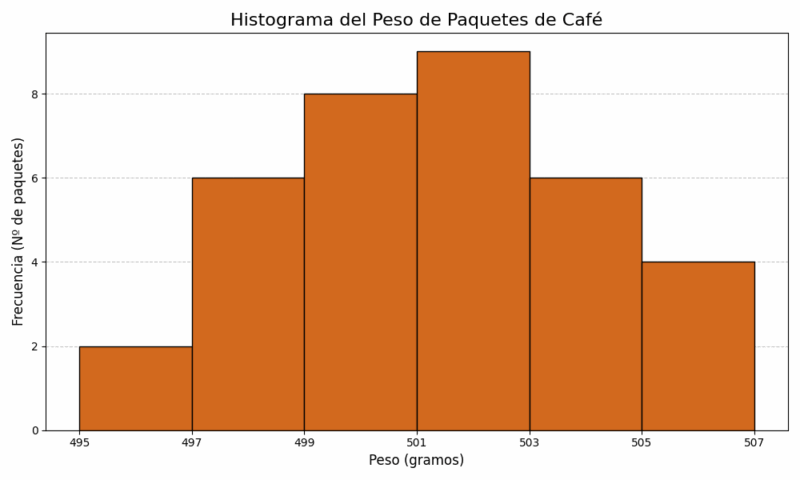
El histograma se dibujaría con 6 barras pegadas, con alturas de 2, 5, 7, 9, 6 y 6. Para el polígono de frecuencias, uniríamos los puntos (496, 2), (498, 5), (500, 7), (502, 9), (504, 6) y (506.5, 6). Lo anclaríamos al eje X con los puntos (494, 0) y (508.5, 0).
La forma del gráfico se asemeja a una distribución simétrica, ligeramente sesgada a la izquierda. El pico se encuentra en el intervalo [501-503), lo que indica que la mayoría de los paquetes tienen un peso muy cercano al valor objetivo de 500 gramos, con una variabilidad controlada. ¡Es un buen resultado para el control de calidad! ✅
Ejemplo 4: Rendimiento en un Examen Difícil de Física Cuántica
Un profesor aplica un examen particularmente desafiante a sus 45 estudiantes de física. Las calificaciones (sobre 100) son las siguientes: 45, 52, 58, 61, 65, 48, 55, 59, 63, 70, 42, 50, 56, 60, 68, 75, 49, 54, 57, 62, 69, 82, 44, 51, 58, 64, 71, 85, 91, 53, 59, 66, 73, 46, 55, 60, 67, 78, 41, 52, 58, 62, 69, 76, 50. El profesor quiere visualizar la distribución de las notas.
Solución:
Paso 1: Número de Datos (N)
El conjunto de datos contiene \(N = 45\) calificaciones.
Paso 2: Rango (R)
Valor Máximo = 91.
Valor Mínimo = 41.
Rango: \(R = 91 - 41 = 50\).
Paso 3: Número de Clases (k)
Regla de Sturges: \(k = 1 + 3.322 \cdot \log_{10}(45) \approx 1 + 3.322 \cdot (1.653) \approx 1 + 5.49 \approx 6.49\).
Redondeamos a \(k=6\) clases.
Paso 4: Amplitud de Clase (A)
\(A = \frac{R}{k} = \frac{50}{6} \approx 8.33\).
Redondeamos hacia arriba a un número conveniente, como \(A=9\).
Paso 5: Tabla de Frecuencias
Empezaremos desde 41.
| Intervalo de Clase (Calificación) | Frecuencia (\(f_i\)) | Marca de Clase (\(x_i\)) |
|---|---|---|
| [41 - 50) | 8 | 45.5 |
| [50 - 59) | 13 | 54.5 |
| [59 - 68) | 12 | 63.5 |
| [68 - 77) | 7 | 72.5 |
| [77 - 86) | 4 | 81.5 |
| [86 - 95) | 1 | 90.5 |
| Total | 45 | - |
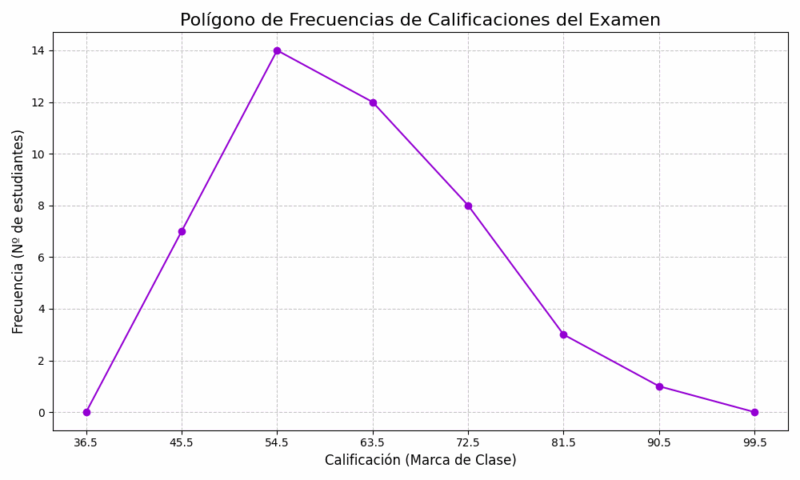
Paso 6: Dibujo e Interpretación
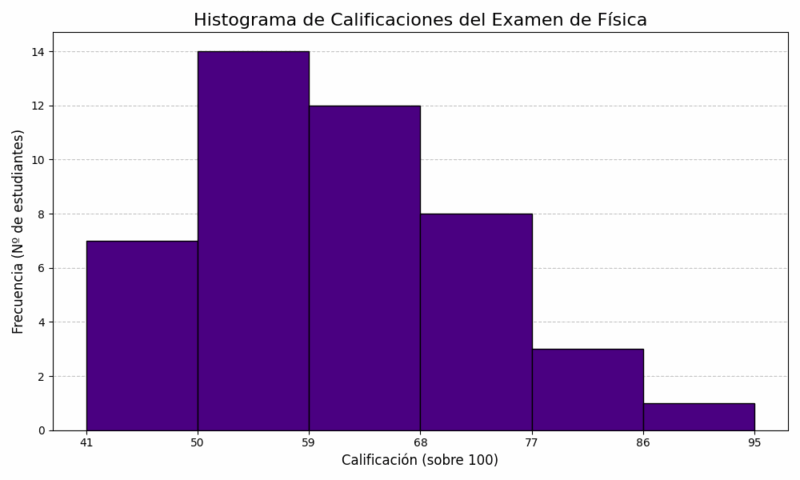 El histograma y el polígono de frecuencias mostrarán un claro sesgo a la derecha (o sesgo positivo). La mayoría de las calificaciones se concentran en la parte baja de la escala (entre 50 y 68), y la frecuencia disminuye drásticamente a medida que las calificaciones aumentan. La larga cola hacia la derecha indica que solo unos pocos estudiantes obtuvieron calificaciones excepcionalmente altas. Esto confirma visualmente que el examen fue, en efecto, muy difícil. 🧠
El histograma y el polígono de frecuencias mostrarán un claro sesgo a la derecha (o sesgo positivo). La mayoría de las calificaciones se concentran en la parte baja de la escala (entre 50 y 68), y la frecuencia disminuye drásticamente a medida que las calificaciones aumentan. La larga cola hacia la derecha indica que solo unos pocos estudiantes obtuvieron calificaciones excepcionalmente altas. Esto confirma visualmente que el examen fue, en efecto, muy difícil. 🧠
Ejemplo 5: Tiempos de Respuesta de un Servicio de Ambulancias
Se analizan los tiempos de respuesta (en minutos) de un servicio de ambulancias para 60 llamadas de emergencia. Los tiempos registrados son: 5.2, 8.1, 6.5, 10.2, 7.8, 9.5, 4.8, 11.1, 12.5, 7.2, 6.9, 8.8, 9.1, 13.0, 5.9, 7.5, 8.3, 10.8, 6.1, 14.2, 5.5, 7.0, 8.6, 9.9, 11.5, 6.8, 7.9, 9.2, 10.5, 12.1, 5.0, 8.2, 6.4, 9.8, 7.4, 10.1, 11.9, 13.5, 5.7, 7.1, 8.9, 9.4, 10.9, 6.6, 7.7, 9.0, 11.2, 12.8, 5.4, 8.0, 6.2, 10.0, 7.3, 11.8, 13.8, 6.0, 7.6, 9.3, 10.6, 12.4. Se busca visualizar la eficiencia del servicio.
Solución:
Paso 1: Número de Datos (N)
Contamos con \(N = 60\) registros de tiempo.
Paso 2: Rango (R)
Valor Máximo = 14.2 min.
Valor Mínimo = 4.8 min.
Rango: \(R = 14.2 - 4.8 = 9.4\).
Paso 3: Número de Clases (k)
Regla de Sturges: \(k = 1 + 3.322 \cdot \log_{10}(60) \approx 1 + 3.322 \cdot (1.778) \approx 1 + 5.90 \approx 6.9\).
Usaremos \(k=7\) clases.
Paso 4: Amplitud de Clase (A)
\(A = \frac{R}{k} = \frac{9.4}{7} \approx 1.34\).
Redondeamos a una amplitud conveniente, por ejemplo, \(A=1.5\) minutos.
Paso 5: Tabla de Frecuencias
Podemos empezar nuestro primer intervalo en 4.5 para cubrir el mínimo.
| Intervalo de Clase (minutos) | Frecuencia (\(f_i\)) | Marca de Clase (\(x_i\)) |
|---|---|---|
| [4.5 - 6.0) | 8 | 5.25 |
| [6.0 - 7.5) | 11 | 6.75 |
| [7.5 - 9.0) | 11 | 8.25 |
| [9.0 - 10.5) | 10 | 9.75 |
| [10.5 - 12.0) | 8 | 11.25 |
| [12.0 - 13.5) | 6 | 12.75 |
| [13.5 - 15.0) | 6 | 14.25 |
| Total | 60 | - |
Paso 6: Dibujo e Interpretación
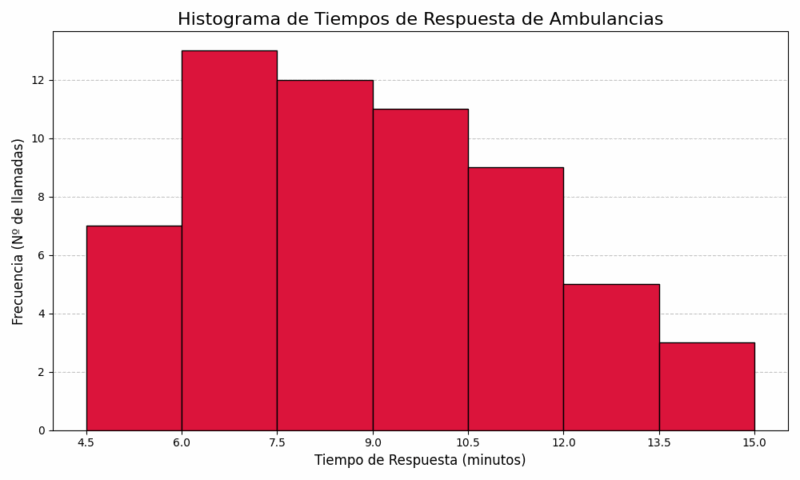
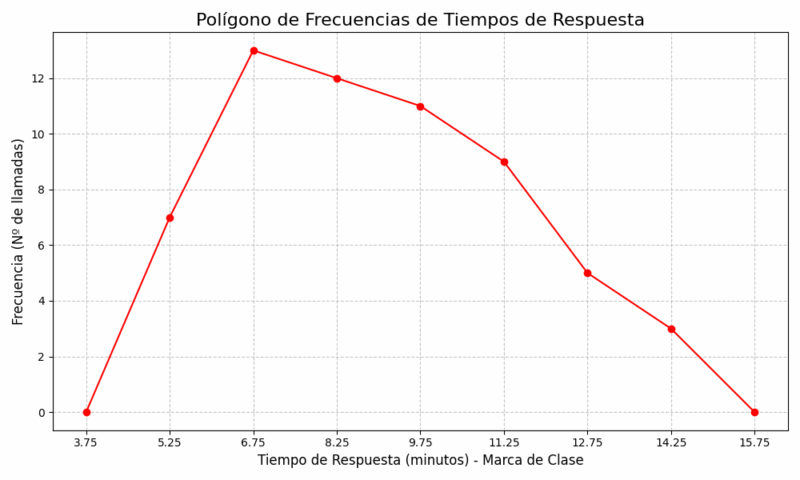
El gráfico resultante mostrará una distribución con un sesgo a la derecha. La mayoría de los tiempos de respuesta se concentran en los intervalos más bajos (entre 6 y 9 minutos), pero existe una cola larga hacia la derecha, indicando que un número significativo de llamadas tardan mucho más en ser atendidas. Este tipo de análisis es vital para que los servicios de emergencia identifiquen casos atípicos y busquen maneras de mejorar su eficiencia en las situaciones más críticas. 🚑
Ejemplo 6: Análisis de Ventas Diarias de una Bebida
Una compañía lanza una nueva bebida que se vende en dos tamaños populares: regular y grande. Se registran las ventas totales de unidades (ambos tamaños combinados) durante 50 días para analizar los patrones de consumo: 15, 18, 21, 23, 16, 19, 22, 40, 42, 45, 17, 20, 24, 41, 44, 14, 18, 21, 25, 39, 43, 46, 16, 19, 22, 40, 45, 15, 20, 23, 41, 46, 17, 21, 24, 38, 42, 44, 18, 19, 23, 40, 43, 45, 16, 20, 22, 41, 44, 17.
Solución:
Paso 1: Número de Datos (N)
Disponemos de \(N = 50\) días de ventas.
Paso 2: Rango (R)
Valor Máximo = 46.
Valor Mínimo = 14.
Rango: \(R = 46 - 14 = 32\).
Paso 3: Número de Clases (k)
Regla de Sturges: \(k = 1 + 3.322 \cdot \log_{10}(50) \approx 1 + 3.322 \cdot (1.699) \approx 1 + 5.64 \approx 6.64\).
Redondeamos a \(k=7\) clases.
Paso 4: Amplitud de Clase (A)
\(A = \frac{R}{k} = \frac{32}{7} \approx 4.57\).
Redondeamos a una amplitud de \(A=5\).
Paso 5: Tabla de Frecuencias
Empezamos en 14.
| Intervalo de Clase (Unidades) | Frecuencia (\(f_i\)) | Marca de Clase (\(x_i\)) |
|---|---|---|
| [14 - 19) | 12 | 16.5 |
| [19 - 24) | 14 | 21.5 |
| [24 - 29) | 2 | 26.5 |
| [29 - 34) | 0 | 31.5 |
| [34 - 39) | 1 | 36.5 |
| [39 - 44) | 11 | 41.5 |
| [44 - 49) | 10 | 46.5 |
| Total | 50 | - |
Paso 6: Dibujo e Interpretación
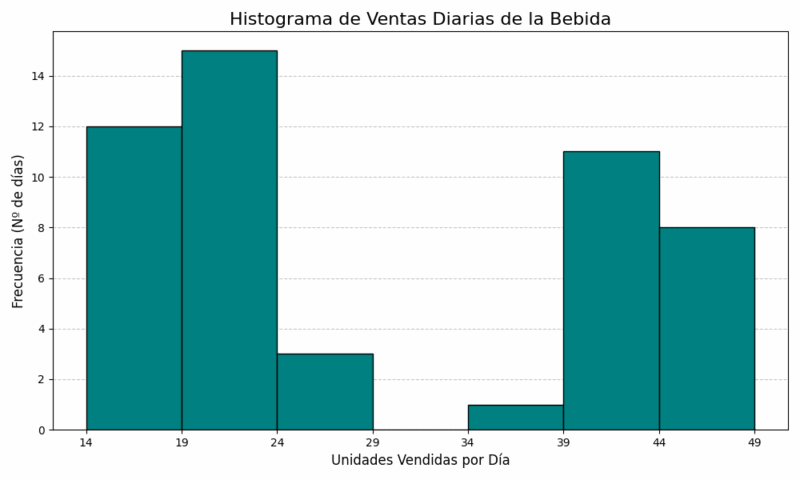
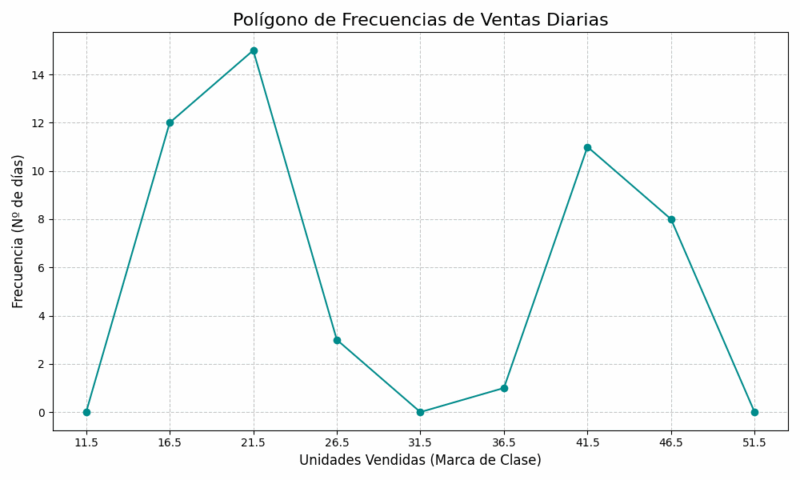
Este es un caso muy interesante. Al dibujar el histograma o el polígono de frecuencias, observaremos una distribución bimodal, es decir, con dos picos claros. Un pico se encuentra en la región de 19-24 unidades y el otro en la región de 39-44 unidades. ¿Qué significa esto? Probablemente los datos provienen de dos grupos de consumidores o patrones de compra diferentes. Por ejemplo, un pico podría representar las ventas en días de semana (quizás la gente compra el tamaño regular) y el otro pico podría corresponder a las ventas en fines de semana (donde se prefiere el tamaño grande). Este tipo de gráfico es extremadamente útil para que el departamento de marketing y logística entienda mejor el comportamiento del consumidor. 📊🥤
Interpretando las Formas: ¿Qué Nos Dicen Nuestros Gráficos? 🧐
Crear los gráficos es solo la mitad del trabajo. La verdadera habilidad de un científico o ingeniero es interpretar lo que esos gráficos significan. La forma de un histograma o polígono de frecuencias nos cuenta una historia sobre nuestros datos.
Distribución Simétrica (o en forma de Campana) 🔔
También conocida como distribución normal. El gráfico tiene un pico central y se extiende de manera simétrica a ambos lados. La mayoría de los datos se agrupan alrededor del centro. Muchos fenómenos naturales, como la altura de las personas o los errores de medición, siguen esta distribución.
Distribución Asimétrica a la Derecha (Sesgo Positivo)
El pico de los datos está a la izquierda, y la "cola" del gráfico se extiende hacia la derecha. Esto significa que la mayoría de los valores son bajos, pero hay algunos valores excepcionalmente altos que estiran la distribución. Un ejemplo podría ser la distribución de los salarios en un país.
Distribución Asimétrica a la Izquierda (Sesgo Negativo)
Es lo opuesto a la anterior. El pico está a la derecha, y la cola se extiende hacia la izquierda. La mayoría de los valores son altos, con algunos valores excepcionalmente bajos. Un ejemplo podría ser las calificaciones en un examen muy fácil.
Distribución Bimodal
El gráfico tiene dos picos. Esto a menudo indica que tu conjunto de datos proviene de dos poblaciones diferentes. Por ejemplo, si mides la altura de un grupo mixto de hombres y mujeres, podrías obtener una distribución bimodal.
Distribución Uniforme
Todas las barras tienen una altura similar, lo que significa que cada rango de valores es igualmente probable. Un ejemplo clásico es el resultado de lanzar un dado muchas veces; cada número del 1 al 6 debería aparecer con una frecuencia similar.
Conclusión: El Poder de la Visualización de Datos
Hemos recorrido un camino completo, desde una lista desordenada de números hasta la creación de dos de los gráficos más informativos en estadística: el histograma y el polígono de frecuencias. Hemos aprendido no solo los pasos mecánicos para su construcción, sino también la lógica detrás de cada decisión, desde elegir el número de clases con la Regla de Sturges hasta interpretar las diversas formas que pueden adoptar nuestros datos.
Dominar estas herramientas es dar el primer paso crucial en cualquier análisis de datos. Te permiten limpiar el ruido, encontrar la señal y contar una historia convincente respaldada por evidencia. Ya sea que estés optimizando un proceso de ingeniería, analizando los resultados de un experimento físico o simplemente tratando de entender el mundo que te rodea, la capacidad de visualizar distribuciones te dará una ventaja invaluable. ¡Ahora tienes el conocimiento para transformar datos crudos en sabiduría visual! ✨
¿Te gustó este contenido?
Únete a nuestra comunidad en WhatsApp o Telegram para recibir nuevos proyectos, tutoriales y noticias exclusivas.
Deja una respuesta

Estos temas te pueden interesar