Multiplicación de Matrices - Ejercicios Resueltos

¡Amigos de Fisimat! Hoy vamos a adentrarnos en una de las operaciones más importantes en el mundo del álgebra lineal: la multiplicación de matrices. Si alguna vez te has preguntado cómo multiplicar estas estructuras rectangulares de números y por qué es tan útil, estás en el mejor lugar. 🤓

La multiplicación multiplicación de matrices es fundamental en campos como la física, la ingeniería, la computación gráfica, la economía e incluso la inteligencia artificial y ciencia de datos. A diferencia de la multiplicación de números simples, tiene sus propias reglas y particularidades que vamos a explorar a fondo.

En este post, cubriremos desde los conceptos básicos hasta ejemplos prácticos paso a paso. ¡Prepárate para dominar esta operación!

¿Qué son las Matrices?

Aunque hemos explicado esto en la categoría de este artículo, las matrices son un arreglo rectangular de números (o elementos) organizados en filas y columnas. Se suelen denotar con letras mayúsculas y sus dimensiones se especifican como "número de filas x número de columnas". Por ejemplo, una matriz A de m × n tiene m filas y n columnas.

Propiedades de la Multiplicación de Matrices

La multiplicación de matrices tiene algunas propiedades importantes que debes conocer. ¡Ojo! Algunas son similares a la multiplicación de números reales, pero hay una diferencia CRUCIAL:

Asocitatividad:

La forma en que agrupas las matrices no afecta el resultado , siempre que el orden se mantenga. Si A, B y C son matrices compatibles para la multiplicación, entonces:

$\displaystyle (AB)C=A(BC)$

Distributividad Respecto a la Suma:

La multiplicación de matrices se distribuye sobre la suma de matrices. Si A, B y C son matrices compatibles para las operaciones:

$\displaystyle \begin{array}{l}\text{A(B+C)=AB+AC}\\\text{(A+B)C=AC+BC}\end{array}$

Existencia de la Matriz Identidad

Existe una matriz especial llamada matriz identidad (I), que al multiplicarla por cualquier matriz A (compatible), deja a A sin cambios:

$\displaystyle \text{AI=IA=A}$

La matriz identidad es una matriz cuadrada (mismo número de filas y columnas) con unos en la diagonal principal y ceros en el resto.

¡MUY IMPORTANTE! No Conmutatividad (en general)

A diferencia de los números reales (3×5 = 5×3), en la multiplicación de matrices, el orden SÍ importa. En la mayoría de los casos, $\displaystyle AB\ne BA$. Incluso puede ser que AB esté definida, pero BA no. ¡Este es un punto clave que debes recordar!

La Regla Fundamental para Multiplicar Matrices

No pueden multiplicarse dos matrices cualesquiera. Existe una regla estricta sobre sus dimensiones para que la multiplicación sea posible.

Imagina que tienes una matriz A de tamaño m × n y quieres multiplicarla por una matriz B de tamaño p × q

La multiplicación AB solo es posible si el número de columnas de la primera matriz (A) es igual al número de filas de la segunda matriz (B). Es decir, si n = p

Si está condición se cumple, la matriz resultante C = AB tendrá un tamaño determinado por el número de filas de la primera matriz (m) y el número de columnas de la segunda matriz (q). Es decir, C será una matriz de m × q (observa la imagen).

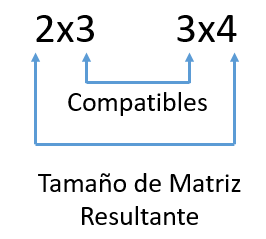
En pocas palabras, basándonos en la imagen de arriba podemos observar que si la matriz A es m × n y la matriz B es n × q. Los "números interiores" deben coincidir. Los "números exteriores" (m y q) dan las dimensiones del tamaño de la matriz resultante.

La Fórmula para Multiplicar Matrices

Si tenemos una matriz A de m × n y una matriz B de n × q , y queremos encontrar la matriz producto C = AB de m × p. ¿cómo calculamos cada elemento de C?

Cada elemento $\displaystyle {{c}_{{ij}}}$ (el elemento en la fila i y la columna j de la matriz B, multiplicando los elementos correspondientes uno a uno, y luego sumando todos esos productos. Esto se conoce como el producto punto entre la fila i de A y la columna j de B. 

Formalmente, el elemento se calcula así:

$\displaystyle {{c}_{{ij}}}={{a}_{{i1}}}{{b}_{{1j}}}+{{a}_{{i2}}}{{b}_{{2j}}}+...+{{a}_{{in}}}{{b}_{{nj}}}=\sum\limits_{{k=1}}^{n}{{{{a}_{{ik}}}{{b}_{{kj}}}}}$

Donde $\displaystyle {{{a}_{{ik}}}}$ es el elemento en la fila i y columna de k de A, y $\displaystyle {{{b}_{{kj}}}}$ es el elemento en la fila k y la columna j de B. La suma se realiza sobre k desde 1 hasta n (el número de columas de A, que es igual al número de filas de B).

Puede parecer un poco abstracto con la fórmula, pero verás que con los ejemplos paso a paso todo quedará mucho más claro.

Ejercicios Resueltos de Multiplicación de Matrices.

Solución.

Verificamos las dimensiones: A es 2x2, B es 2x2.

El número de columnas de A (2) es igual al número de filas de B (2).

La multiplicación es posible y la matriz resultante será 2x2.

Sea $C = AB = \begin{pmatrix} c_{11} & c_{12} \\ c_{21} & c_{22} \end{pmatrix}$.

Calculamos cada elemento (lo explicamos paso a paso) :

$c_{11} = (\text{fila 1 de A}) \cdot (\text{columna 1 de B})$
$c_{11} = (1 \times 5) + (2 \times 7) = 5 + 14 = 19$

$c_{12} = (\text{fila 1 de A}) \cdot (\text{columna 2 de B})$
$c_{12} = (1 \times 6) + (2 \times 8) = 6 + 16 = 22$

$c_{21} = (\text{fila 2 de A}) \cdot (\text{columna 1 de B})$
$c_{21} = (3 \times 5) + (4 \times 7) = 15 + 28 = 43$

$c_{22} = (\text{fila 2 de A}) \cdot (\text{columna 2 de B})$
$c_{22} = (3 \times 6) + (4 \times 8) = 18 + 32 = 50$

Por lo tanto, la matriz producto es:

$$AB = \begin{pmatrix}
19 & 22 \\
43 & 50
\end{pmatrix}$$

Solución:

Verificamos las dimensiones: A es 3x3, B es 3x3.

El número de columnas de A (3) es igual al número de filas de B (3).

La multiplicación es posible y la matriz resultante será 3x3.

Sea $C = AB = \begin{pmatrix} c_{11} & c_{12} & c_{13} \\ c_{21} & c_{22} & c_{23} \\ c_{31} & c_{32} & c_{33} \end{pmatrix}$.

Calculamos cada elemento:

$c_{11} = (1 \times 2) + (0 \times 0) + (2 \times 1) = 2 + 0 + 2 = 4$
$c_{12} = (1 \times 1) + (0 \times -1) + (2 \times 0) = 1 + 0 + 0 = 1$
$c_{13} = (1 \times 0) + (0 \times 2) + (2 \times 3) = 0 + 0 + 6 = 6$

$c_{21} = (-1 \times 2) + (3 \times 0) + (1 \times 1) = -2 + 0 + 1 = -1$
$c_{22} = (-1 \times 1) + (3 \times -1) + (1 \times 0) = -1 - 3 + 0 = -4$
$c_{23} = (-1 \times 0) + (3 \times 2) + (1 \times 3) = 0 + 6 + 3 = 9$

$c_{31} = (0 \times 2) + (1 \times 0) + (0 \times 1) = 0 + 0 + 0 = 0$
$c_{32} = (0 \times 1) + (1 \times -1) + (0 \times 0) = 0 - 1 + 0 = -1$
$c_{33} = (0 \times 0) + (1 \times 2) + (0 \times 3) = 0 + 2 + 0 = 2$

Por lo tanto, la matriz producto es:

$$AB = \begin{pmatrix}
4 & 1 & 6 \\
-1 & -4 & 9 \\
0 & -1 & 2
\end{pmatrix}$$

Solución.

Verificamos las dimensiones: A es 2x3, B es 3x2.

El número de columnas de A (3) es igual al número de filas de B (3).

La multiplicación es posible y la matriz resultante será 2x2.

Sea $C = AB = \begin{pmatrix} c_{11} & c_{12} \\ c_{21} & c_{22} \end{pmatrix}$.

Calculamos cada elemento:

$c_{11} = (1 \times 7) + (2 \times 9) + (3 \times 2) = 7 + 18 + 6 = 31$
$c_{12} = (1 \times 8) + (2 \times 1) + (3 \times 3) = 8 + 2 + 9 = 19$

$c_{21} = (4 \times 7) + (5 \times 9) + (6 \times 2) = 28 + 45 + 12 = 85$
$c_{22} = (4 \times 8) + (5 \times 1) + (6 \times 3) = 32 + 5 + 18 = 55$

Por lo tanto, la matriz producto es:

$$AB = \begin{pmatrix}
31 & 19 \\
85 & 55
\end{pmatrix}$$

Solución.

Verificamos las dimensiones: A es 4x4, B es 4x4.

El número de columnas de A (4) es igual al número de filas de B (4).

La multiplicación es posible y la matriz resultante será 4x4.

Sea $C = AB$.

Calculamos los elementos de la primera fila:

$c_{11} = (1 \times 1) + (0 \times 1) + (0 \times 1) + (0 \times 1) = 1 + 0 + 0 + 0 = 1$
$c_{12} = (1 \times 1) + (0 \times 1) + (0 \times 1) + (0 \times 1) = 1 + 0 + 0 + 0 = 1$
$c_{13} = (1 \times 1) + (0 \times 1) + (0 \times 1) + (0 \times 1) = 1 + 0 + 0 + 0 = 1$
$c_{14} = (1 \times 1) + (0 \times 1) + (0 \times 1) + (0 \times 1) = 1 + 0 + 0 + 0 = 1$

La primera fila de la matriz producto es $[1 \ 1 \ 1 \ 1]$.

Calculamos el primer elemento de la segunda fila:

$c_{21} = (0 \times 1) + (2 \times 1) + (0 \times 1) + (0 \times 1) = 0 + 2 + 0 + 0 = 2$

De manera similar, calculamos los otros elementos de la segunda fila:

$c_{22} = (0 \times 1) + (2 \times 1) + (0 \times 1) + (0 \times 1) = 2$
$c_{23} = (0 \times 1) + (2 \times 1) + (0 \times 1) + (0 \times 1) = 2$
$c_{24} = (0 \times 1) + (2 \times 1) + (0 \times 1) + (0 \times 1) = 2$

La segunda fila de la matriz producto es $[2 \ 2 \ 2 \ 2]$.

Siguiendo el mismo patrón (fila $i$ de A con columna $j$ de B), donde la matriz A es diagonal, la fila $i$ de la matriz producto tendrá el elemento $a_{ii}$ repetido en cada posición.

La tercera fila será $[3 \ 3 \ 3 \ 3]$.
La cuarta fila será $[4 \ 4 \ 4 \ 4]$.

Por lo tanto, la matriz producto es:

$$AB = \begin{pmatrix}
1 & 1 & 1 & 1 \\
2 & 2 & 2 & 2 \\
3 & 3 & 3 & 3 \\
4 & 4 & 4 & 4
\end{pmatrix}$$

Solución.

Para que el producto $AB$ sea posible, el número de columnas de la matriz A debe ser igual al número de filas de la matriz B.

La matriz A tiene 2 columnas.
La matriz B tiene 3 filas.

Como el número de columnas de A (2) no es igual al número de filas de B (3), la multiplicación de matrices $AB$ no está definida. No es posible calcular el producto $AB$

Solución.

Verificamos las dimensiones para el producto $BA$: B es 3x2, A es 2x3.

El número de columnas de B (2) es igual al número de filas de A (2).

La multiplicación $BA$ es posible y la matriz resultante será 3x3.

Sea $D = BA = \begin{pmatrix} d_{11} & d_{12} & d_{13} \\ d_{21} & d_{22} & d_{23} \\ d_{31} & d_{32} & d_{33} \end{pmatrix}$.

Calculamos cada elemento:

$d_{11} = (\text{fila 1 de B}) \cdot (\text{columna 1 de A})$
$d_{11} = (7 \times 1) + (8 \times 4) = 7 + 32 = 39$

$d_{12} = (\text{fila 1 de B}) \cdot (\text{columna 2 de A})$
$d_{12} = (7 \times 2) + (8 \times 5) = 14 + 40 = 54$

$d_{13} = (\text{fila 1 de B}) \cdot (\text{columna 3 de A})$
$d_{13} = (7 \times 3) + (8 \times 6) = 21 + 48 = 69$

$d_{21} = (\text{fila 2 de B}) \cdot (\text{columna 1 de A})$
$d_{21} = (9 \times 1) + (1 \times 4) = 9 + 4 = 13$

$d_{22} = (\text{fila 2 de B}) \cdot (\text{columna 2 de A})$
$d_{22} = (9 \times 2) + (1 \times 5) = 18 + 5 = 23$

$d_{23} = (\text{fila 2 de B}) \cdot (\text{columna 3 de A})$
$d_{23} = (9 \times 3) + (1 \times 6) = 27 + 6 = 33$

$d_{31} = (\text{fila 3 de B}) \cdot (\text{columna 1 de A})$
$d_{31} = (2 \times 1) + (3 \times 4) = 2 + 12 = 14$

$d_{32} = (\text{fila 3 de B}) \cdot (\text{columna 2 de A})$
$d_{32} = (2 \times 2) + (3 \times 5) = 4 + 15 = 19$

$d_{33} = (\text{fila 3 de B}) \cdot (\text{columna 3 de A})$
$d_{33} = (2 \times 3) + (3 \times 6) = 6 + 18 = 24$

Por lo tanto, la matriz producto $BA$ es:

$$BA = \begin{pmatrix}
39 & 54 & 69 \\
13 & 23 & 33 \\
14 & 19 & 24
\end{pmatrix}$$

Del Problema 3, obtuvimos $AB = \begin{pmatrix} 31 & 19 \\ 85 & 55 \end{pmatrix}$.

Comparamos $AB$ (tamaño 2x2) con $BA$ (tamaño 3x3). Son matrices de diferente tamaño y con elementos completamente distintos. Esto confirma la propiedad de no conmutatividad: $AB \neq BA$

Solucion.

Verificamos las dimensiones: A es 2x2, B es 2x2.

El numero de columnas de A (2) es igual al numero de filas de B (2).

La multiplicacion es posible y la matriz resultante sera 2x2.

Sea $C = AB = \begin{pmatrix} c_{11} & c_{12} \\ c_{21} & c_{22} \end{pmatrix}$.

Calculamos cada elemento:

$c_{11} = (\text{fila 1 de A}) \cdot (\text{columna 1 de B})$
$c_{11} = (-1 \times 0) + (5 \times 2) = 0 + 10 = 10$

$c_{12} = (\text{fila 1 de A}) \cdot (\text{columna 2 de B})$
$c_{12} = (-1 \times 1) + (5 \times 4) = -1 + 20 = 19$

$c_{21} = (\text{fila 2 de A}) \cdot (\text{columna 1 de B})$
$c_{21} = (3 \times 0) + (-2 \times 2) = 0 - 4 = -4$

$c_{22} = (\text{fila 2 de A}) \cdot (\text{columna 2 de B})$
$c_{22} = (3 \times 1) + (-2 \times 4) = 3 - 8 = -5$

Por lo tanto, la matriz producto es:

$$AB = \begin{pmatrix}
10 & 19 \\
-4 & -5
\end{pmatrix}$$

Solucion.

Verificamos las dimensiones: C es 2x3, D es 3x2.

El numero de columnas de C (3) es igual al numero de filas de D (3).

La multiplicacion es posible y la matriz resultante sera 2x2.

Sea $E = CD = \begin{pmatrix} e_{11} & e_{12} \\ e_{21} & e_{22} \end{pmatrix}$.

Calculamos cada elemento:

$e_{11} = (\text{fila 1 de C}) \cdot (\text{columna 1 de D})$
$e_{11} = (2 \times 1) + (-1 \times -2) + (3 \times 3) = 2 + 2 + 9 = 13$

$e_{12} = (\text{fila 1 de C}) \cdot (\text{columna 2 de D})$
$e_{12} = (2 \times 0) + (-1 \times 5) + (3 \times -1) = 0 - 5 - 3 = -8$

$e_{21} = (\text{fila 2 de C}) \cdot (\text{columna 1 de D})$
$e_{21} = (0 \times 1) + (4 \times -2) + (1 \times 3) = 0 - 8 + 3 = -5$

$e_{22} = (\text{fila 2 de C}) \cdot (\text{columna 2 de D})$
$e_{22} = (0 \times 0) + (4 \times 5) + (1 \times -1) = 0 + 20 - 1 = 19$

Por lo tanto, la matriz producto es:

$$CD = \begin{pmatrix}
13 & -8 \\
-5 & 19
\end{pmatrix}$$

Solucion:

Primero calculamos $EF$.

Dimensiones: E es 1x2, F es 2x1.

El numero de columnas de E (2) es igual al numero de filas de F (2).

La multiplicacion EF es posible y la matriz resultante sera 1x1.

Sea $G = EF = (g_{11})$.

Calculamos el elemento:

$g_{11} = (\text{fila 1 de E}) \cdot (\text{columna 1 de F})$
$g_{11} = (1 \times 3) + (2 \times 4) = 3 + 8 = 11$

El producto EF es una matriz 1x1 (que a menudo se trata como un escalar):

$$EF = \begin{pmatrix} 11 \end{pmatrix}$$

Ahora calculamos $FE$.

Dimensiones: F es 2x1, E es 1x2.

El numero de columnas de F (1) es igual al numero de filas de E (1).

La multiplicacion FE es posible y la matriz resultante sera 2x2.

Sea $H = FE = \begin{pmatrix} h_{11} & h_{12} \\ h_{21} & h_{22} \end{pmatrix}$.

Calculamos cada elemento:

$h_{11} = (\text{fila 1 de F}) \cdot (\text{columna 1 de E})$
$h_{11} = (3 \times 1) = 3$

$h_{12} = (\text{fila 1 de F}) \cdot (\text{columna 2 de E})$
$h_{12} = (3 \times 2) = 6$

$h_{21} = (\text{fila 2 de F}) \cdot (\text{columna 1 de E})$
$h_{21} = (4 \times 1) = 4$

$h_{22} = (\text{fila 2 de F}) \cdot (\text{columna 2 de E})$
$h_{22} = (4 \times 2) = 8$

El producto FE es la matriz 2x2:

$$FE = \begin{pmatrix}
3 & 6 \\
4 & 8
\end{pmatrix}$$

Observamos que los productos $EF$ (1x1) y $FE$ (2x2) no son del mismo tamaño, lo que refuerza la idea de que el orden en la multiplicacion de matrices importa ($EF \neq FE$). Ambos resultados son matrices, aunque una matriz 1x1 a veces se identifica con el escalar.

Solucion.

Primero calculamos $GI$.

Dimensiones: G es 2x2, I es 2x2.

La multiplicacion es posible y el resultado sera 2x2.

Sea $J = GI = \begin{pmatrix} j_{11} & j_{12} \\ j_{21} & j_{22} \end{pmatrix}$.

Calculamos cada elemento:

$j_{11} = (4 \times 1) + (0 \times 0) = 4 + 0 = 4$
$j_{12} = (4 \times 0) + (0 \times 1) = 0 + 0 = 0$
$j_{21} = (1 \times 1) + (-3 \times 0) = 1 + 0 = 1$
$j_{22} = (1 \times 0) + (-3 \times 1) = 0 - 3 = -3$

$$GI = \begin{pmatrix}
4 & 0 \\
1 & -3
\end{pmatrix}$$

Ahora calculamos $IG$.

Dimensiones: I es 2x2, G es 2x2.

La multiplicacion es posible y el resultado sera 2x2.

Sea $K = IG = \begin{pmatrix} k_{11} & k_{12} \\ k_{21} & k_{22} \end{pmatrix}$.

Calculamos cada elemento:

$k_{11} = (1 \times 4) + (0 \times 1) = 4 + 0 = 4$
$k_{12} = (1 \times 0) + (0 \times -3) = 0 + 0 = 0$
$k_{21} = (0 \times 4) + (1 \times 1) = 0 + 1 = 1$
$k_{22} = (0 \times 0) + (1 \times -3) = 0 - 3 = -3$

$$IG = \begin{pmatrix}
4 & 0 \\
1 & -3
\end{pmatrix}$$

Observamos que $GI = G$ y $IG = G$. Ambas multiplicaciones resultan en la matriz original G. Esto demuestra la propiedad de la matriz identidad: multiplicarla por una matriz (compatible) no cambia la matriz original.

Solucion:

Para que el producto $HJ$ sea posible, el numero de columnas de la matriz H debe ser igual al numero de filas de la matriz J.

La matriz H tiene 3 columnas.
La matriz J tiene 2 filas.

Como el numero de columnas de H (3) no es igual al numero de filas de J (2), la multiplicacion de matrices $HJ$ no esta definida. No es posible calcular el producto $HJ$.

Solucion:

Verificamos las dimensiones: K es 3x3, L es 3x1.

El numero de columnas de K (3) es igual al numero de filas de L (3).

La multiplicacion es posible y la matriz resultante sera 3x1 (un vector columna).

Sea $M = KL = \begin{pmatrix} m_1 \\ m_2 \\ m_3 \end{pmatrix}$.

Calculamos cada elemento (cada elemento es el producto punto de una fila de K por la unica columna de L):

$m_1 = (\text{fila 1 de K}) \cdot (\text{columna 1 de L})$
$m_1 = (1 \times 0) + (0 \times 1) + (-1 \times 0) = 0 + 0 + 0 = 0$

$m_2 = (\text{fila 2 de K}) \cdot (\text{columna 1 de L})$
$m_2 = (0 \times 0) + (2 \times 1) + (0 \times 0) = 0 + 2 + 0 = 2$

$m_3 = (\text{fila 3 de K}) \cdot (\text{columna 1 de L})$
$m_3 = (-1 \times 0) + (0 \times 1) + (3 \times 0) = 0 + 0 + 0 = 0$

Por lo tanto, la matriz producto es el vector columna:

$$KL = \begin{pmatrix}
0 \\
2 \\
0
\end{pmatrix}$$

Conclusión

Hemos cubierto los aspectos esenciales de la multiplicación de matrices, su definición, propiedades (incluyendo la importancia de la no conmutatividad), la regla de compatibilidad basada en las dimensiones y la fórmula para calcular cada elemento del producto. A través de ejemplos paso a paso de diferentes tamaños, has visto cómo aplicar la teoría en la práctica.

La multiplicación de matrices es una herramienta poderosa con amplias aplicaciones. Dominarla es un paso crucial en tu camino en el estudio del álgebra lineal y muchas otras disciplinas. 🤓