Conversión de Fracciones Impropias a Mixtas - Ejercicios Resueltos

En el fascinante mundo de las fracciones, no siempre todas las cantidades se representan de la misma forma. A veces, nos encontramos con fracciones donde el numerador es mayor o igual que el denominador; a estas las llamamos fracciones impropias. Aunque matemáticamente correctas, pueden ser un poco difíciles de visualizar o interpretar en situaciones de la vida real. Es aquí donde entran en juego los números mixtos, una forma más intuitiva de representar esas mismas cantidades, combinando una parte entera con una fracción propia.

Dominar la conversión entre fracciones impropias y números mixtos, y viceversa, es una habilidad fundamental que te permitirá trabajar con mayor fluidez en matemáticas. Facilita la comprensión de las magnitudes, simplifica cálculos y es esencial para resolver problemas cotidianos que involucran "más de un todo", como repartir ingredientes en la cocina o gestionar materiales en proyectos de ingeniería. En este artículo, aprenderás a realizar estas conversiones de manera sencilla y eficiente.

Para entender la conversión, primero recordemos la definición de cada tipo de fracción.

Fracciones Impropias

Una fracción impropia es aquella en la que el numerador es mayor o igual que el denominador. Esto significa que la fracción representa una cantidad igual o mayor que la unidad (un entero).

Ejemplos:

$\frac{5}{3}$, $\frac{7}{2}$, $\frac{4}{4}$

Visualmente, si tienes una pizza dividida en 3 partes y tomas 5, necesitas más de una pizza completa.

Números Mixtos

Un número mixto es una combinación de un número entero y una fracción propia. La parte entera indica cuántas unidades completas hay, y la fracción propia indica la parte restante de la unidad.

Ejemplos:

$1\frac{2}{3}$ (un entero y dos tercios), $3\frac{1}{2}$ (tres enteros y un medio)

Conversión de Fracciones Impropias a Números Mixtos

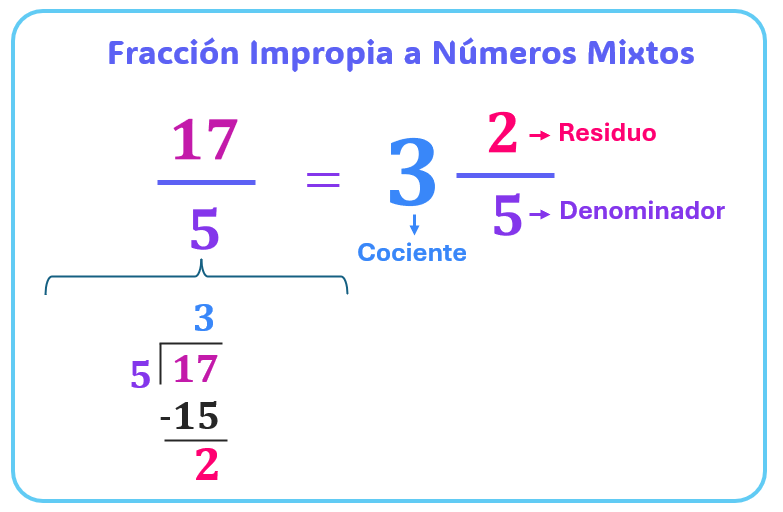
Para convertir una fracción impropia a un número mixto, el proceso se basa en la división.

1. Divide el numerador por el denominador.
2. El cociente de la división será la parte entera del número mixto.
3. El resto de la división será el numerador de la fracción propia.
4. El denominador original de la fracción impropia se mantiene como el denominador de la fracción propia.

• Ejemplo: Convertir $\frac{17}{5}$ a número mixto.
  Dividimos $17 \div 5$:
  $$17 \div 5 = 3 \text{ con un resto de } 2$$
  • Cociente: 3 (parte entera)
  • Resto: 2 (nuevo numerador)
  • Denominador original: 5 (se mantiene)

  Por lo tanto, $\frac{17}{5} = 3\frac{2}{5}$.

Conversión de Números Mixtos a Fracciones Impropias

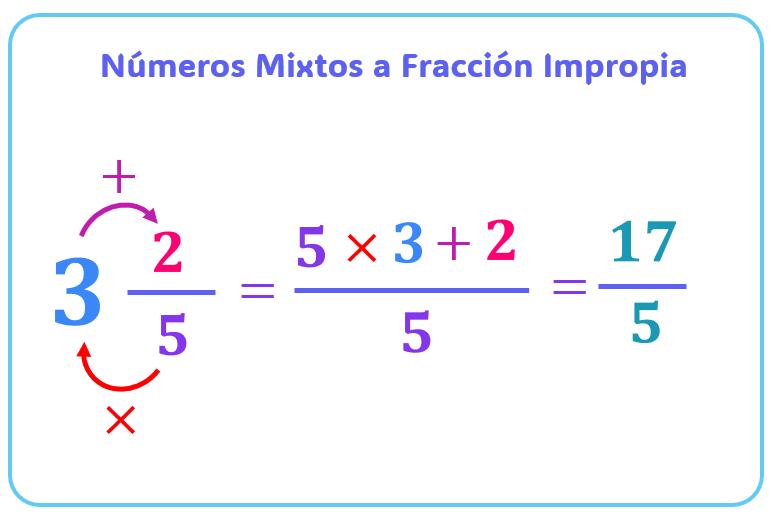
Para convertir un número mixto a una fracción impropia, realizamos el proceso inverso.

1. Multiplica la parte entera del número mixto por el denominador de la fracción propia.
2. Suma el numerador de la fracción propia al resultado del paso anterior. Este será el nuevo numerador de la fracción impropia.
3. El denominador de la fracción propia se mantiene como el denominador de la fracción impropia.

• Ejemplo: Convertir $2\frac{3}{4}$ a fracción impropia.
  • Multiplicar parte entera por denominador: $2 \times 4 = 8$.
  • Sumar el numerador: $8 + 3 = 11$. (Nuevo numerador)
  • Mantener el denominador: 4.

  Por lo tanto, $2\frac{3}{4} = \frac{11}{4}$.

Ejercicios Resueltos

Afianza tus habilidades con estos ejercicios detallados de conversión.

Solución

▷ Paso 1 Dividir el numerador por el denominador.

$$9 \div 2$$

Al dividir $9$ entre $2$, obtenemos un cociente de $4$ y un resto de $1$.

▷ Paso 2 Formar el número mixto.

El cociente ($4$) es la parte entera.

El resto ($1$) es el nuevo numerador.

El denominador original ($2$) se mantiene.

Por lo tanto, $\frac{9}{2} = 4\frac{1}{2}$.

Solución

▷ Paso 1 Multiplicar la parte entera por el denominador.

$$5 \times 3 = 15$$

▷ Paso 2 Sumar el numerador de la fracción propia al resultado anterior.

$$15 + 1 = 16$$

▷ Paso 3 Formar la fracción impropia.

El resultado del paso 2 ($16$) es el nuevo numerador.

El denominador original ($3$) se mantiene.

Por lo tanto, $5\frac{1}{3} = \frac{16}{3}$.

Solución

▷ Paso 1 Dividir el numerador por el denominador.

$$13 \div 6$$

$13$ dividido por $6$ es $2$ con un resto de $1$.

▷ Paso 2 Formar el número mixto.

Cociente = $2$

Resto = $1$

Denominador = $6$

Por lo tanto, $\frac{13}{6} = 2\frac{1}{6}$.

Solución

▷ Paso 1 Multiplicar la parte entera por el denominador.

$$1 \times 8 = 8$$

▷ Paso 2 Sumar el numerador al producto.

$$8 + 7 = 15$$

▷ Paso 3 Formar la fracción impropia.

El nuevo numerador es $15$. El denominador se mantiene ($8$).

Por lo tanto, $1\frac{7}{8} = \frac{15}{8}$.

Solución

▷ Paso 1 Dividir el numerador por el denominador.

$$20 \div 3$$

$20$ dividido por $3$ es $6$ con un resto de $2$.

▷ Paso 2 Formar el número mixto.

Cociente = $6$

Resto = $2$

Denominador = $3$

Por lo tanto, $\frac{20}{3} = 6\frac{2}{3}$.

Solución

▷ Paso 1 Multiplicar la parte entera por el denominador.

$$4 \times 5 = 20$$

▷ Paso 2 Sumar el numerador al producto.

$$20 + 2 = 22$$

▷ Paso 3 Formar la fracción impropia.

El nuevo numerador es $22$. El denominador se mantiene ($5$).

Por lo tanto, $4\frac{2}{5} = \frac{22}{5}$.

Solución

▷ Paso 1 Determinar si es impropia.

El numerador ($10$) es mayor que el denominador ($5$), por lo tanto, sí es una fracción impropia.

▷ Paso 2 Convertir a número mixto (o entero en este caso).

Dividir el numerador por el denominador:

$$10 \div 5 = 2$$

El cociente es $2$ y el resto es $0$. Cuando el resto es $0$, la fracción impropia se convierte en un número entero.

Por lo tanto, $\frac{10}{5} = 2$.

Solución

▷ Paso 1 Representar como fracción impropia.

El denominador es el número total de porciones en que se divide un pastel ($8$).

El numerador es el número de porciones que comió María ($11$).

Fracción impropia: $\frac{11}{8}$.

▷ Paso 2 Convertir la fracción impropia a número mixto.

Dividir $11$ entre $8$:

$$11 \div 8 = 1 \text{ con un resto de } 3$$

Cociente = $1$ (parte entera)

Resto = $3$ (nuevo numerador)

Denominador = $8$ (se mantiene)

Número mixto: $1\frac{3}{8}$.

Respuesta: La cantidad se representa como $\frac{11}{8}$ (fracción impropia) y $1\frac{3}{8}$ (número mixto).

Solución

Para saber cuántos "cuartos de kilómetro" corre, debemos convertir el número mixto a una fracción impropia con denominador 4.

▷ Paso 1 Multiplicar la parte entera por el denominador.

$$2 \times 4 = 8$$

▷ Paso 2 Sumar el numerador al producto.

$$8 + 1 = 9$$

▷ Paso 3 Formar la fracción impropia.

El nuevo numerador es $9$. El denominador se mantiene ($4$).

Por lo tanto, $2\frac{1}{4} = \frac{9}{4}$.

Respuesta: El deportista corre $\frac{9}{4}$ de kilómetro en total, es decir, 9 cuartos de kilómetro.

Solución

Para resolver este problema, primero convertimos el número mixto a una fracción impropia, y luego lo multiplicamos por la cantidad de galletas por paquete.

▷ Paso 1 Convertir el número mixto $3\frac{5}{6}$ a fracción impropia.

Multiplicar la parte entera por el denominador: $3 \times 6 = 18$.
Sumar el numerador: $18 + 5 = 23$.
La fracción impropia es $\frac{23}{6}$.

▷ Paso 2 Multiplicar la fracción impropia por la cantidad de galletas por paquete.

$$\frac{23}{6} \times 6$$
$$ = \frac{23 \times 6}{6}$$
$$ = 23$$

Respuesta: Tenemos 23 galletas en total.

Conclusión

La capacidad de convertir entre fracciones impropias y números mixtos es más que un simple ejercicio matemático; es una herramienta práctica que te permite expresar y entender cantidades de manera flexible. Las fracciones impropias son concisas para los cálculos, mientras que los números mixtos ofrecen una representación más intuitiva de "cuántas unidades completas" y "qué parte adicional" hay.

Dominar estas conversiones te empodera para abordar problemas de la vida real con mayor claridad, desde la dosificación en recetas hasta la comprensión de datos en ingeniería. Al sentirte cómodo con ambos formatos, abres la puerta a una manipulación más eficiente de los números y fortaleces tu base aritmética para desafíos más complejos. ¡Sigue practicando para que estas conversiones se conviertan en algo natural!