Integrales Definidas - Ejercicios Resueltos
Hemos llegado al tema de las integrales definidas, uno de los temas más solicitados por nuestros seguidores y del que ya hemos preparado varios videos en nuestras redes sociales. No obstante, nos hemos tomado el tiempo de desarrollar este artículo para explicarlas de forma ordenada, progresiva y textual, aunque es importante reconocer la importancia de las Sumas de Riemann para el cálculo de áreas, a veces el procedimiento puede parecer muy largo y difícil. Isaac Newton descubrió un método más sencillo para evaluar las integrales, aunque años después, Leibniz realizó el mismo hallazgo. Esto también se conoce como el Teorema Fundamental del Cálculo.
En publicaciones anteriores vimos las integrales indefinidas, las cuales no generan un valor numérico como resultado, sino una función general F(x) que representa una familia de curvas. ¿Recuerdas? Ahora bien, cuando una integral sí genera un valor numérico específico, hablamos de una integral definida. Este valor representa, entre otras cosas, el área bajo una curva en un intervalo determinado.
¿Qué es una integral definida?
Una integral definida es una operación matemática que permite calcular el valor total de una función dentro de un intervalo específico. En otras palabras, nos indica cuánto "acumula" una función entre dos puntos, desde un valor inicial x = a hasta un valor final x = b
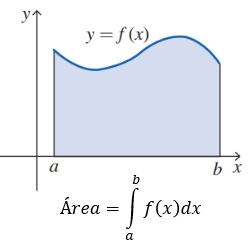
Este tipo de integral se representa con límites de integración y da como resultado un número real.
¿Cuál es la fórmula de la integral definida?
La notación estándar es:
$\displaystyle \int\limits_{a}^{b}{{f(x)dx}}$
Dónde:
f(x) es la función que se va a integrar
a es el límite inferior de integración
b es el límite superior de integración
dx indica que la variable de integración es x
¿Cómo se resuelve una integral definida?
El procedimiento para resolver una integral definida consta de dos pasos fundamentales:
- Integrar la función: se busca una función primitiva F(x) tal que F'(x) = f(x)
- Evaluar los límites: se sustituye en la función primita los valores del intervalo [a,b], restando:
$\displaystyle \int\limits_{a}^{b}{{f(x)dx}}=F(b)-F(a)$
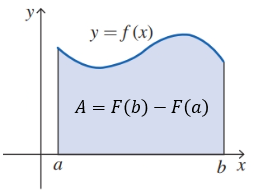
Nota: El símbolo +C que aparece en las integrales indefinidas no se usa en las definidas, ya que al restar F(b) - F(a), cualquier constante se cancela.
Ejercicios Resuelto de Integrales Definidas
Vamos a realizar algunos ejemplos y en dado caso que tengas problemas para entender en el blog, lo hemos hecho video en nuestras redes sociales.
\(\int_0^2 x^2 \, dx\)
Solución:
Primero, encontramos la antiderivada de \(x^2\):
\[
\int x^2 \, dx = \frac{x^3}{3} + C
\]
Evaluamos la integral definida usando el teorema fundamental del cálculo:
\[
\int_0^2 x^2 \, dx = \left[ \frac{x^3}{3} \right]_0^2
\]
Sustituimos los límites:
\[
\frac{2^3}{3} - \frac{0^3}{3} = \frac{8}{3} - 0 = \frac{8}{3}
\]
Por lo tanto, la solución es:
\[
\boxed{\int_0^2 x^2 \, dx = \frac{8}{3}}
\]
¿Tuviste problemas para entender la integral?, no te preocupes mira el video paso a paso 👇
| 🎵 Ver en TikTok | 📷 Ver en Instagram |
\(\int_0^2 x \, dx\)
Solución:
Primero, encontramos la antiderivada de \(x\):
\[
\int x \, dx = \frac{x^2}{2} + C
\]
Evaluamos la integral definida usando el teorema fundamental del cálculo:
\[
\int_0^2 x \, dx = \left[ \frac{x^2}{2} \right]_0^2
\]
Sustituimos los límites:
\[
\frac{2^2}{2} - \frac{0^2}{2} = \frac{4}{2} - 0 = 2
\]
Por lo tanto, la solución es:
\[
\boxed{\int_0^2 x \, dx = 2}
\]
¿Tuviste problemas para entender la integral?, no te preocupes mira el video paso a paso 👇
| 🎵 Ver en TikTok | 📷 Ver en Instagram |
\(\int_1^3 (6x^2 + 4x - 1) \, dx\)
Solución:
Integramos término a término:
\[
\int (6x^2 + 4x - 1) \, dx = \int 6x^2 \, dx + \int 4x \, dx - \int 1 \, dx
\]
Calculamos cada integral:
\[
\int 6x^2 \, dx = 6 \cdot \frac{x^3}{3} = 2x^3,\quad \int 4x \, dx = 4 \cdot \frac{x^2}{2} = 2x^2,\quad \int 1 \, dx = x
\]
Entonces, la antiderivada es:
\[
2x^3 + 2x^2 - x
\]
Aplicamos el teorema fundamental del cálculo:
\[
\int_1^3 (6x^2 + 4x - 1) \, dx = \left[2x^3 + 2x^2 - x\right]_1^3
\]
Evaluamos en los límites:
\[
\text{En } x = 3: \quad 2(3)^3 + 2(3)^2 - 3 = 54 + 18 - 3 = 69
\]
\[
\text{En } x = 1: \quad 2(1)^3 + 2(1)^2 - 1 = 2 + 2 - 1 = 3
\]
Restamos los valores:
\[
69 - 3 = 66
\]
Por lo tanto, la solución es:
\[
\boxed{\int_1^3 (6x^2 + 4x - 1) \, dx = 66}
\]
¿Tuviste problemas para entender la integral?, no te preocupes mira el video paso a paso 👇
| 🎵 Ver en TikTok | 📷 Ver en Instagram |
\(\int_1^2 \frac{1}{x} \, dx\)
Solución:
La integral de \(\frac{1}{x}\) es:
\[
\int \frac{1}{x} \, dx = \ln|x| + C
\]
Aplicamos el teorema fundamental del cálculo:
\[
\int_1^2 \frac{1}{x} \, dx = \left[\ln|x|\right]_1^2
\]
Evaluamos en los límites:
\[
\ln|2| - \ln|1| = \ln(2) - \ln(1)
\]
Sabemos que \(\ln(1) = 0\), así que:
\[
\ln(2) - 0 = \ln(2)
\]
Por lo tanto, la solución es:
\[
\boxed{\int_1^2 \frac{1}{x} \, dx = \ln(2)}
\]
¿Tuviste problemas para entender la integral?, no te preocupes mira el video paso a paso 👇
| 🎵 Ver en TikTok | 📷 Ver en Instagram |
\(\int_0^4 \sqrt{x} \, dx\)
Solución:
Recordamos que \(\sqrt{x} = x^{1/2}\), así que escribimos la integral en forma de potencia:
\[
\int_0^4 \sqrt{x} \, dx = \int_0^4 x^{1/2} \, dx
\]
Aplicamos la regla de potencias para integrar:
\[
\int x^{1/2} \, dx = \frac{x^{3/2}}{3/2} = \frac{2}{3}x^{3/2}
\]
Aplicamos el teorema fundamental del cálculo:
\[
\int_0^4 \sqrt{x} \, dx = \left[\frac{2}{3}x^{3/2}\right]_0^4
\]
Evaluamos los límites:
\[
\frac{2}{3}(4)^{3/2} - \frac{2}{3}(0)^{3/2}
\]
Sabemos que \(4^{3/2} = (\sqrt{4})^3 = 2^3 = 8\), entonces:
\[
\frac{2}{3}(8) - 0 = \frac{16}{3}
\]
Por lo tanto, la solución es:
\[
\boxed{\int_0^4 \sqrt{x} \, dx = \frac{16}{3}}
\]
¿Tuviste problemas para entender la integral?, no te preocupes mira el video paso a paso 👇
| 🎵 Ver en TikTok | 📷 Ver en Instagram |
\(\int_0^{\frac{\pi}{2}} \sin(x) \, dx\)
Solución:
La integral de \(\sin(x)\) es:
\[
\int \sin(x) \, dx = -\cos(x) + C
\]
Aplicamos el teorema fundamental del cálculo:
\[
\int_0^{\frac{\pi}{2}} \sin(x) \, dx = \left[-\cos(x)\right]_0^{\frac{\pi}{2}}
\]
Evaluamos en los límites:
\[
-\cos\left(\frac{\pi}{2}\right) + \cos(0) = -0 + 1 = 1
\]
Por lo tanto, la solución es:
\[
\boxed{\int_0^{\frac{\pi}{2}} \sin(x) \, dx = 1}
\]
¿Tuviste problemas para entender la integral?, no te preocupes mira el video paso a paso 👇
| 🎵 Ver en TikTok | 📷 Ver en Instagram |
\(\int_1^e \frac{1}{x} \, dx\)
Solución:
La integral de \(\frac{1}{x}\) es:
\[
\int \frac{1}{x} \, dx = \ln|x| + C
\]
Aplicamos el teorema fundamental del cálculo:
\[
\int_1^e \frac{1}{x} \, dx = \left[\ln|x|\right]_1^e
\]
Evaluamos en los límites:
\[
\ln(e) - \ln(1)
\]
Sabemos que \(\ln(e) = 1\) y \(\ln(1) = 0\), así que:
\[
1 - 0 = 1
\]
Por lo tanto, la solución es:
\[
\boxed{\int_1^e \frac{1}{x} \, dx = 1}
\]
¿Tuviste problemas para entender la integral?, no te preocupes mira el video paso a paso 👇
| 🎵 Ver en TikTok | 📷 Ver en Instagram |
\(\int_0^3 \left( \frac{x^3}{2} - 3x \right) \, dx\)
Solución:
Aplicamos la integral término a término:
\[
\int \left( \frac{x^3}{2} - 3x \right) dx = \frac{1}{2} \int x^3 \, dx - 3 \int x \, dx
\]
Resolvemos cada parte:
\[
\frac{1}{2} \cdot \frac{x^4}{4} - 3 \cdot \frac{x^2}{2} = \frac{x^4}{8} - \frac{3x^2}{2}
\]
Aplicamos el teorema fundamental del cálculo:
\[
\int_0^3 \left( \frac{x^3}{2} - 3x \right) dx = \left[\frac{x^4}{8} - \frac{3x^2}{2} \right]_0^3
\]
Evaluamos en los límites:
\[
\left( \frac{3^4}{8} - \frac{3 \cdot 3^2}{2} \right) - \left( \frac{0^4}{8} - \frac{3 \cdot 0^2}{2} \right)
\]
\[
= \left( \frac{81}{8} - \frac{27}{2} \right) - 0
\]
Hacemos la resta con común denominador:
\[
\frac{81}{8} - \frac{108}{8} = -\frac{27}{8}
\]
Por lo tanto, la solución es:
\[
\boxed{\int_0^3 \left( \frac{x^3}{2} - 3x \right) \, dx = -\frac{27}{8}}
\]
¿Tuviste problemas para entender la integral?, no te preocupes mira el video paso a paso 👇
| 🎵 Ver en TikTok | 📷 Ver en Instagram |
\(\int_1^3 (2x - 1) \, dx\)
Solución:
Aplicamos la integral término a término:
\[
\int (2x - 1) \, dx = \int 2x \, dx - \int 1 \, dx
\]
Resolvemos cada parte:
\[
\int 2x \, dx = x^2 \quad \text{y} \quad \int 1 \, dx = x
\]
Por lo tanto, la integral es:
\[
\int (2x - 1) \, dx = x^2 - x
\]
Aplicamos el teorema fundamental del cálculo:
\[
\int_1^3 (2x - 1) \, dx = \left[x^2 - x\right]_1^3
\]
Evaluamos en los límites:
\[
\left(3^2 - 3\right) - \left(1^2 - 1\right)
\]
\[
= (9 - 3) - (1 - 1) = 6 - 0 = 6
\]
Por lo tanto, la solución es:
\[
\boxed{\int_1^3 (2x - 1) \, dx = 6}
\]
¿Tuviste problemas para entender la integral?, no te preocupes mira el video paso a paso 👇
| 🎵 Ver en TikTok | 📷 Ver en Instagram |
\(\int_0^2 \left( 4x - e^x \right) \, dx\)
Solución:
Aplicamos la integral término a término:
\[
\int \left( 4x - e^x \right) dx = \int 4x \, dx - \int e^x \, dx
\]
Resolvemos cada parte:
\[
\int 4x \, dx = 2x^2 \quad \text{y} \quad \int e^x \, dx = e^x
\]
Por lo tanto, la integral es:
\[
\int \left( 4x - e^x \right) dx = 2x^2 - e^x
\]
Aplicamos el teorema fundamental del cálculo:
\[
\int_0^2 \left( 4x - e^x \right) dx = \left[2x^2 - e^x\right]_0^2
\]
Evaluamos en los límites:
\[
\left(2(2^2) - e^2\right) - \left(2(0^2) - e^0\right)
\]
\[
= \left(2(4) - e^2\right) - \left(0 - 1\right)
\]
\[
= (8 - e^2) - (-1) = 8 - e^2 + 1 = 9 - e^2
\]
Por lo tanto, la solución es:
\[
\boxed{\int_0^2 \left( 4x - e^x \right) \, dx = 9 - e^2}
\]
¿Tuviste problemas para entender la integral?, no te preocupes mira el video paso a paso 👇
| 🎵 Ver en TikTok | 📷 Ver en Instagram |
\(\int_0^{\frac{\pi}{2}} \left( \cos x - \sin x \right) \, dx\)
Solución:
Aplicamos la integral término a término:
\[
\int \left( \cos x - \sin x \right) dx = \int \cos x \, dx - \int \sin x \, dx
\]
Resolvemos cada parte:
\[
\int \cos x \, dx = \sin x \quad \text{y} \quad \int \sin x \, dx = -\cos x
\]
Por lo tanto, la integral es:
\[
\int \left( \cos x - \sin x \right) dx = \sin x + \cos x
\]
Aplicamos el teorema fundamental del cálculo:
\[
\int_0^{\frac{\pi}{2}} \left( \cos x - \sin x \right) \, dx = \left[\sin x + \cos x\right]_0^{\frac{\pi}{2}}
\]
Evaluamos en los límites:
\[
\left(\sin\left(\frac{\pi}{2}\right) + \cos\left(\frac{\pi}{2}\right)\right) - \left(\sin(0) + \cos(0)\right)
\]
Sabemos que:
\[
\sin\left(\frac{\pi}{2}\right) = 1, \quad \cos\left(\frac{\pi}{2}\right) = 0, \quad \sin(0) = 0, \quad \cos(0) = 1
\]
Entonces:
\[
(1 + 0) - (0 + 1) = 1 - 1 = 0
\]
Por lo tanto, la solución es:
\[
\boxed{\int_0^{\frac{\pi}{2}} \left( \cos x - \sin x \right) \, dx = 0}
\]
¿Tuviste problemas para entender la integral?, no te preocupes mira el video paso a paso 👇
| 🎵 Ver en TikTok | 📷 Ver en Instagram |
Conclusión
Las integrales definidas nos permiten calcular el área bajo una curva dentro de un intervalo específico. Aplicando el Teorema Fundamental del Cálculo, podemos encontrar el valor exacto de esa área usando antiderivadas, lo que convierte este proceso en una herramienta poderosa tanto en las matemáticas puras como en sus aplicaciones reales.
Dominar este tema no solo refuerza las bases del cálculo, sino que también nos prepara para resolver problemas prácticos en física, economía o ingeniería. En resumen, integrar es mucho más que seguir pasos: es comprender cómo cambian las cosas y cómo se acumulan a lo largo del tiempo o del espacio.
¿Te gustó este contenido?
Únete a nuestra comunidad en WhatsApp o Telegram para recibir nuevos proyectos, tutoriales y noticias exclusivas.
Deja una respuesta

Estos temas te pueden interesar