Multiplicación de un Escalar por una Matriz - Ejercicios Resueltos

¡Hola, Amigos de Fisimat! Después de haber explorado juntos cómo sumar matrices y entender su estructura, es momento de dar el siguiente paso lógico: la multiplicación de una matriz por un escalar. Esta es una operación fundamental y muy utilizada en diversos campos de la ingeniería, la física y la computación.

Quizás te preguntes, ¿qué es exactamente un "escalar"? y esto se debe al gran matemático William Rowan Hamilton. Él utilizó el término "escalar" en su trabajo sobre cuaterniones para referirse a la parte real de estos números, que podía "escalar" en la línea numérica desde el infinito negativo hasta el positivo. 😎

Para nuestros propósitos en el álgebra lineal básica, cuando hablamos de un escalar, nos referimos simplemente a un número real (como el 2, -5, 0.5, 4/3, π, etc.). Este número "escalará" o modificará la magnitud de todos los elementos de nuestra matriz.

¿Qué es un Escalar?

Como mencionamos, en el contexto del álgebra de matrices que estamos estudiando (especialmente a nivel de bachillerato e introducción a la ingeniería), un escalar es simplemente un número real. Puede ser positivo, negativo, cero, entero, fraccionario, ¡lo que sea! Este número único interactuará con cada uno de los elementos de una matriz.

La idea de que un solo número pueda afectar a toda una colección de datos (los elementos de la matriz) de manera uniforme es lo que hace que esta operación sea tan útil y sencilla de comprender.

¿Cómo se Multiplica una Matriz por un Escalar?

La regla para multiplicar una matriz por un escalar es muy directa: cada elemento de la matriz se multiplica individualmente por dicho escalar.

Si tenemos una matriz A y un escalar α (la letra griega "alfa" se usa comúnmente para representar escalares), el producto αA será una nueva matriz del mismo tamaño que A, donde cada elemento original $\displaystyle {{a}_{{ij}}}$ ha sido reemplazado por $\displaystyle \alpha {{a}_{{ij}}}$

Fórmula General

Sea $\displaystyle \alpha $ un escalar y $\displaystyle A$ una matriz de $\displaystyle m\times n$ elementos:

$\displaystyle A=\left( {\begin{array}{*{20}{c}} {{{a}_{{11}}}} & {{{a}_{{12}}}} & \cdots & {{{a}_{{1n}}}} \\ {{{a}_{{21}}}} & {{{a}_{{22}}}} & \cdots & {{{a}_{{2n}}}} \\ \vdots & \vdots & \ddots & \vdots \\ {{{a}_{{m1}}}} & {{{a}_{{m2}}}} & \cdots & {{{a}_{{mn}}}} \end{array}} \right)$

El producto escalar $\displaystyle \alpha $ por la matriz A es:

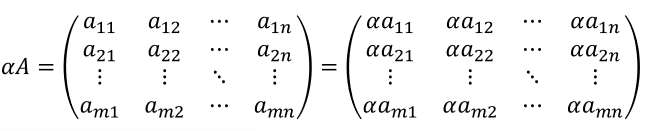
la fórmula nos dice exactamente lo que comentamos: toma el escalar $\alpha$ y multiplícalo por cada uno de los elementos que componen la matriz $A$. ¡Así de simple!

Propiedades de la Multiplicación por un Escalar

Esta operación tiene algunas propiedades importantes que son muy útiles y te recordarán a las propiedades de los números reales. Sean A y B matrices del mismo tamaño, y α y β (beta) escalares:

Propiedad Distributiva (escalar sobre suma de matrices):

$\displaystyle \alpha \left( {A+B} \right)=\alpha A+\alpha B$

(Puedes distribuir el escalar a cada matriz antes de sumar los resultados, o sumar las matrices primero y luego multiplicar por el escalar).

Propiedad Distributiva (suma de escalares sobre una matriz):

$\displaystyle \left( {\alpha +\beta } \right)A=\alpha A+\beta A$

(Puedes sumar los escalares primero y luego multiplicar la matriz, o multiplicar la matriz por cada escalar y luego sumar las matrices resultantes).

Propiedad Asociativa (con producto de escalares):

$\displaystyle \left( {\alpha \beta } \right)A=\alpha \left( {\beta A} \right)$

(Puedes multiplicar los escalares entre sí primero, o multiplicar la matriz por un escalar y luego el resultado por el otro escalar).

Elemento Neutro Multiplicativo (escalar 1):

$\displaystyle 1A=A$

(Multiplicar cualquier matriz por el escalar 1 la deja sin cambios).

Multiplicación por el Escalar Cero:

$\displaystyle 0A=0$

(Multiplicar cualquier matriz por el escalar 0 resulta en la matriz cero, donde todos los elementos son cero).

Multiplicación por el Escalar -1:

$\displaystyle \left( {-1} \right)A=-A$

(Multiplicar por -1 nos da la matriz opuesta, lo que es útil para la resta de matrices: A−B=A+(−1)B ).

Estas propiedades son fundamentales y facilitan mucho los cálculos y las demostraciones en álgebra lineal.

Ejercicios Resueltos de Multiplicación de un Escalar por una Matriz

\[
A = \begin{pmatrix}
1 & -2 \\
3 & 0
\end{pmatrix}
\]

Solución:
Multiplicamos cada elemento de la matriz \( A \) por el escalar \( \alpha = 4 \):

\[
4A = 4 \begin{pmatrix}
1 & -2 \\
3 & 0
\end{pmatrix}
= \begin{pmatrix}
4 \times 1 & 4 \times (-2) \\
4 \times 3 & 4 \times 0
\end{pmatrix}
= \begin{pmatrix}
4 & -8 \\
12 & 0
\end{pmatrix}
\]

El resultado es:
\[
4A = \begin{pmatrix}
4 & -8 \\
12 & 0
\end{pmatrix}
\]

\[
B = \begin{pmatrix}
2 & 0 \\
-1 & 5
\end{pmatrix}
\]

Solución:
Multiplicamos cada elemento de la matriz \( B \) por el escalar \( \beta = -3 \):

\[
-3B = -3 \begin{pmatrix}
2 & 0 \\
-1 & 5
\end{pmatrix}
= \begin{pmatrix}
-3 \times 2 & -3 \times 0 \\
-3 \times (-1) & -3 \times 5
\end{pmatrix}
= \begin{pmatrix}
-6 & 0 \\
3 & -15
\end{pmatrix}
\]

El resultado es:
\[
-3B = \begin{pmatrix}
-6 & 0 \\
3 & -15
\end{pmatrix}
\]

\[
C = \begin{pmatrix}
7 & -3 \\
2 & 9
\end{pmatrix}
\]

Solución:
Multiplicamos cada entrada de la matriz \( C \) por el escalar \( \gamma = 0 \):

\[
0C = 0 \begin{pmatrix}
7 & -3 \\
2 & 9
\end{pmatrix}
= \begin{pmatrix}
0 \times 7 & 0 \times (-3) \\
0 \times 2 & 0 \times 9
\end{pmatrix}
= \begin{pmatrix}
0 & 0 \\
0 & 0
\end{pmatrix}
\]

El resultado es:
\[
0C = \begin{pmatrix}
0 & 0 \\
0 & 0
\end{pmatrix}
\]

\[
D = \begin{pmatrix}
4 & -1 \\
6 & 3
\end{pmatrix}
\]

Solución:
Multiplicamos cada elemento de la matriz \( D \) por el escalar \( \delta = 2 \):

\[
2D = 2 \begin{pmatrix}
4 & -1 \\
6 & 3
\end{pmatrix}
= \begin{pmatrix}
2 \times 4 & 2 \times (-1) \\
2 \times 6 & 2 \times 3
\end{pmatrix}
= \begin{pmatrix}
8 & -2 \\
12 & 6
\end{pmatrix}
\]

El resultado es:
\[
2D = \begin{pmatrix}
8 & -2 \\
12 & 6
\end{pmatrix}
\]

\[
E = \begin{pmatrix}
0 & 2 \\
-4 & 5
\end{pmatrix}
\]

Solución:
Multiplicamos cada entrada de la matriz \( E \) por el escalar \( \epsilon = -1 \):

\[
-1E = -1 \begin{pmatrix}
0 & 2 \\
-4 & 5
\end{pmatrix}
= \begin{pmatrix}
-1 \times 0 & -1 \times 2 \\
-1 \times (-4) & -1 \times 5
\end{pmatrix}
= \begin{pmatrix}
0 & -2 \\
4 & -5
\end{pmatrix}
\]

El resultado es:
\[
-1E = \begin{pmatrix}
0 & -2 \\
4 & -5
\end{pmatrix}
\]

\[
F = \begin{pmatrix}
4 & -6 \\
8 & 2
\end{pmatrix}
\]

Solución:
Multiplicamos cada elemento de la matriz \( F \) por \( \dfrac{1}{2} \):

\[
\dfrac{1}{2}F = \dfrac{1}{2} \begin{pmatrix}
4 & -6 \\
8 & 2
\end{pmatrix}
= \begin{pmatrix}
\dfrac{1}{2} \cdot 4 & \dfrac{1}{2} \cdot (-6) \\
\dfrac{1}{2} \cdot 8 & \dfrac{1}{2} \cdot 2
\end{pmatrix}
= \begin{pmatrix}
2 & -3 \\
4 & 1
\end{pmatrix}
\]

El resultado es:
\[
\dfrac{1}{2}F = \begin{pmatrix}
2 & -3 \\
4 & 1
\end{pmatrix}
\]

\[
G = \begin{pmatrix}
1 & 0 \\
-2 & \sqrt{2}
\end{pmatrix}
\]

Solución:
Multiplicamos cada elemento de \( G \) por \( \sqrt{3} \):

\[
\sqrt{3}G = \sqrt{3} \begin{pmatrix}
1 & 0 \\
-2 & \sqrt{2}
\end{pmatrix}
= \begin{pmatrix}
\sqrt{3} \cdot 1 & \sqrt{3} \cdot 0 \\
\sqrt{3} \cdot (-2) & \sqrt{3} \cdot \sqrt{2}
\end{pmatrix}
= \begin{pmatrix}
\sqrt{3} & 0 \\
-2\sqrt{3} & \sqrt{6}
\end{pmatrix}
\]

El resultado es:
\[
\sqrt{3}G = \begin{pmatrix}
\sqrt{3} & 0 \\
-2\sqrt{3} & \sqrt{6}
\end{pmatrix}
\]

\[
H = \begin{pmatrix}
\frac{2}{3} & 1 \\
-1 & \frac{4}{5}
\end{pmatrix}
\]

Solución:
Multiplicamos cada entrada de \( H \) por \( -\dfrac{3}{4} \):

\[
-\dfrac{3}{4}H = -\dfrac{3}{4} \begin{pmatrix}
\frac{2}{3} & 1 \\
-1 & \frac{4}{5}
\end{pmatrix}
= \begin{pmatrix}
-\dfrac{3}{4} \cdot \dfrac{2}{3} & -\dfrac{3}{4} \cdot 1 \\
-\dfrac{3}{4} \cdot (-1) & -\dfrac{3}{4} \cdot \dfrac{4}{5}
\end{pmatrix}
= \begin{pmatrix}
-\dfrac{1}{2} & -\dfrac{3}{4} \\
\dfrac{3}{4} & -\dfrac{3}{5}
\end{pmatrix}
\]

El resultado es:
\[
-\dfrac{3}{4}H = \begin{pmatrix}
-\dfrac{1}{2} & -\dfrac{3}{4} \\
\dfrac{3}{4} & -\dfrac{3}{5}
\end{pmatrix}
\]