Problema 1 de Dilatación Superficial

En este ejemplo de los problemas resueltos para ejercicios de práctica del tema de Dilatación Superficial, es importante tener en cuenta el uso correcto de la fórmula, es por eso que se realizan los ejercicios paso a paso con su solución correspondiente. Recuerde que con este tipo de ejemplos el alumno podrá corroborar su respuesta y verificar si ha llegado al mismo resultado. 😊👇

Nivel de Dificultad: ⭐⭐

Problema 3. Una lámina de acero tiene un área de 2m² a una temperatura de 8°C ¿Cuál será su área final al elevarse su temperatura a 38°C?

Problema de dilatación superficial

Solución:

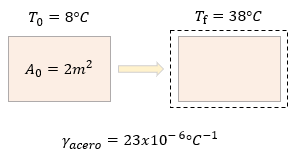
La solución del problema es sumamente claro, nos piden el área final después de que la temperatura aumentó a 38°C, además de ello nos proporcionan los datos en la imagen de forma muy precisa, así como también el coeficiente de dilatación superficial del acero.

Obtener el área final de la lámina de acero

Datos:

$\displaystyle {{T}_{0}}=8{}^\circ C$

$\displaystyle {{T}_{f}}=38{}^\circ C$

$\displaystyle {{A}_{0}}=2{{m}^{2}}$

$\displaystyle {{\gamma }_{acero}}=23x{{10}^{-6}}{}^\circ {{C}^{-1}}$

a) Obteniendo el área final

Para comenzar a obtener el área final, veamos la fórmula principal:

$\displaystyle {{A}_{f}}={{A}_{0}}[1+\gamma \left( {{T}_{f}}-{{T}_{0}} \right)]$

Sustituyendo nuestros datos en la fórmula:

$\displaystyle {{A}_{f}}=2{{m}^{2}}[1+23x{{10}^{-6}}{}^\circ {{C}^{-1}}\left( 38{}^\circ C-8{}^\circ C \right)]$

Realizando la diferencia de temperaturas ΔT

$\displaystyle {{A}_{f}}=2{{m}^{2}}[1+23x{{10}^{-6}}{}^\circ {{C}^{-1}}\left( 30{}^\circ C \right)]$

Multiplicando lo que nos dio de diferencia de temperaturas por el coeficiente de dilatación superficial

$\displaystyle {{A}_{f}}=2{{m}^{2}}\left( 1+0.00069 \right)$

Sumando a la unidad

$\displaystyle {{A}_{f}}=2{{m}^{2}}\left( 1.00069 \right)$

Multiplicando por 2m²

$\displaystyle {{A}_{f}}=2.00138{{m}^{2}}$

Es decir que tenemos un área final de 2.00138 m²

Resultado:

$\displaystyle {{A}_{f}}=2.00138{{m}^{2}}$

Deja una respuesta Cancelar la respuesta

Subir

🤓 Únete a nuestro canal de WhatsApp 👉UNIRME

+