Problema 1 de Dilatación Volumétrica

En este ejemplo de los problemas resueltos para ejercicios de práctica del tema de Dilatación Cúbica o Dilatación Volumétrica, es importante tener en cuenta el uso correcto de la fórmula, es por eso que se realizan los ejercicios paso a paso con su solución correspondiente. Recuerde que con este tipo de ejemplos el alumno podrá corroborar su respuesta y verificar si ha llegado al mismo resultado. 😊👇

Nivel de Dificultad: ⭐⭐

Problema 4. Una esfera hueca de acero a 28°C tiene un volumen de 0.4 m³, calcular a) ¿qué volumen final tendrá a -6°C en m³ y en litros? b) ¿Cuánto disminuyó su volumen en litros?

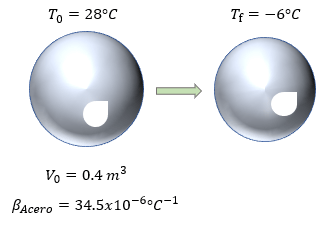
Problema de dilatación volumétrica

Solución:

El ejercicio es sumamente sencillo, no requiere de realizar muchos análisis al respecto, solamente debemos observar que contamos con la mayor cantidad de datos listos para sustituir en nuestra fórmula de dilatación volumétrica, por ejemplo contamos con temperatura inicial y final, así como el volumen inicial y el coeficiente de dilatación cúbica del acero. Posteriormente nos piden resolver la cantidad de volumen que disminuyó la esfera. Veamos entonces.

Obtener el volumen final de la esfera
Obtener cuanto disminuyó su volumen en litros.

Datos:

$\displaystyle {{\beta }_{Acero}}=34.5x{{10}^{-6}}{}^\circ {{C}^{-1}}$

$\displaystyle {{T}_{0}}=28{}^\circ C$

$\displaystyle {{T}_{f}}=-6{}^\circ C$

$\displaystyle {{V}_{0}}=0.4{{m}^{3}}$

a) Obteniendo el volumen final de la esfera

Basándonos en la fórmula de volumen final, obtenemos:

$\displaystyle {{V}_{f}}={{V}_{0}}[1+\beta \left( {{T}_{f}}-{{T}_{0}} \right)]$

Sustituyendo nuestros datos en la fórmula:

$\displaystyle {{V}_{f}}=0.4{{m}^{3}}[1+34.5x{{10}^{-6}}{}^\circ {{C}^{-1}}\left( -6{}^\circ C-28{}^\circ C \right)]$

$\displaystyle {{V}_{f}}=0.4{{m}^{3}}[1+34.5x{{10}^{-6}}{}^\circ {{C}^{-1}}\left( -34{}^\circ C \right)]$

Realizando el producto del coeficiente de dilatación volumétrica por la temperatura

$\displaystyle {{V}_{f}}=0.4{{m}^{3}}\left( 1-0.001173 \right)$

Realizando la resta:

$\displaystyle {{V}_{f}}=0.4{{m}^{3}}\left( 0.998827 \right)$

Multiplicando, finalmente obtenemos:

$\displaystyle {{V}_{f}}=0.3995308{{m}^{3}}$

Es decir que nuestro volumen final es de 0.3995308 m³

Pasando los metros cúbicos a litros mediante su factor de conversión, obtenemos:

$\displaystyle {{V}_{f}}=0.3995308{{m}^{3}}\left( \frac{1000l}{1{{m}^{3}}} \right)=399.5308l$

Es decir, que tenemos 399.5308 litros

b) Obteniendo cuánto disminuyó la esfera en litros

Para saber cuanto disminuyó la esfera en litros, es importante pasar el volumen inicial a litros. Entonces:

$\displaystyle {{V}_{0}}=0.4{{m}^{3}}\left( \frac{1000l}{1{{m}^{3}}} \right)=400l$

Realizamos la diferencia:

$\displaystyle \Delta V=399.5308l-400l=-0.4692l$

Es decir, -0.4692 litros

Respuestas:

$\displaystyle \begin{array}{l}{{V}_{f}}=0.3995308{{m}^{3}}=399.5308l\\\Delta V=-0.4692l\end{array}$

Deja una respuesta Cancelar la respuesta