Solución Problema 3 de Densidad y Peso Específico

Para este tipo de problemas de Densidad y Peso específico que implica hacer uso de los datos que proporciona el ejercicio es de vital importancia tener los valores finales para así poder resolver los siguientes ejemplos que dependen del primer resultado.

Nivel de Dificultad: ⭐⭐⭐

Problema 7. Calcular la densidad de un prisma rectangular cuyas dimensiones son: largo = 6 cm, ancho = 5 cm y alto = 3 cm. Tiene una masa de 300 gramos. Calcular el volumen que ocupará un objeto de la misma sustancia si tiene una masa de 100 gramos.

Problema 3 de densidad y peso especifico

Solución:

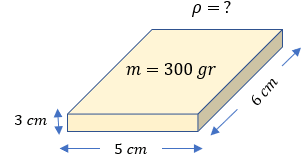
Si observamos el prisma rectangular, vemos que nos proporcionan dos datos muy importantes: la medida de los lados que multiplicadas todas nos proporcionaría el volumen, y adicionalmente también nos provee la masa.

Obtener la densidad del prisma
El volumen de un objeto con la misma densidad

Datos:

$\displaystyle V=(0.03m)(0.05m)(0.06m)=0.00009{{m}^{3}}$

$\displaystyle m=300g$

a) Obtener la densidad del prisma

Para calcular la densidad, aplicamos la fórmula que ya conocemos:

$\displaystyle \rho =\frac{m}{V}$

Sustituyendo en nuestra fórmula:

$\displaystyle \rho =\frac{m}{V}=\frac{0.3kg}{0.00009{{m}^{3}}}=3333.3\frac{kg}{{{m}^{3}}}$

Podemos notar que hemos convertido los 300 gramos a kilogramos. Entonces:

La densidad es de 3,333.3 kg/m³

b) Obtener el volumen de un objeto con la misma densidad

Si sabemos que la densidad es de 3,333.3 kg/m³ , y que la masa es de 100 gramos. Entonces la formula sería:

$\displaystyle V=\frac{m}{\rho }=\frac{0.1kg}{3333.3\frac{kg}{{{m}^{3}}}}=30x{{10}^{-6}}{{m}^{3}}$

Es decir, un volumen de 30 x 10 ^(-6) m³

Resultados:

$\displaystyle \begin{array}{l}\rho =3333.3\frac{kg}{{{m}^{3}}}\\{{V}_{2}}=30x{{10}^{-6}}{{m}^{3}}\end{array}$

1 Comentarios Publicados

EDWIN OTONIEL HERRERA dice:

1 mayo, 2023 a las 3:25 pm

Saludos cordiales desde Panajachel, Sololá

Responder

Deja una respuesta Cancelar la respuesta

Subir

🤓 Únete a nuestro canal de WhatsApp 👉UNIRME

+