Problema 3 de Dilatación Superficial

Con este tercer problema de Dilatación Superficial, el alumno finalmente refuerza el uso de la fórmula utilizando los despejes de la fórmula, ir viendo las diversas variables que se pueden obtener a través de la fórmula de dilatación superficial y que resuelve todo tipo de problemas que se puede encontrar en algún examen o tarea. 😊👇

Nivel de Dificultad: ⭐⭐⭐

Problema 5. En un laboratorio un científico estudia el fenómeno de dilatación, en su experimento desea encajar perfectamente un anillo de cobre en un cilindro. El anillo tiene un radio de 2cm a 20°C y un coeficiente de dilatación lineal de 17x10^(-6)°C ¯¹ ; determine a que temperatura el anillo debe ser calentado para que sea introducido en un cilindro cuya área de base es igual a 15cm², considere π = 3.14

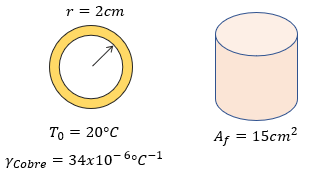
Problema de dilatacion superficial

Solución:

Sin duda este problema es más complejo que los dos anteriores, por el simple hecho de que no nos proporciona demasiados datos como para colocarlos en la fórmula y poder resolver de manera directa, entonces debemos analizar bien el ejercicio y poder determinar de que manera podemos encontrar la temperatura final del anillo.

Encontrar la temperatura final del anillo

Datos:

$\displaystyle r=2cm$

$\displaystyle {{T}_{0}}=20{}^\circ C$

$\displaystyle {{A}_{f}}=15c{{m}^{2}}$

$\displaystyle \lambda =2\alpha =2(17x{{10}^{-6}}{}^\circ {{C}^{-1}})=34x{{10}^{-6}}{}^\circ {{C}^{-1}}$

$\displaystyle {{A}_{f}}=15c{{m}^{2}}$

a) Encontrar la temperatura final

Si observamos el área inicial es justamente el área del anillo, para calcular el área del anillo debemos aplicar la fórmula del área de un circulo, entonces:

$\displaystyle {{A}_{0}}=\pi {{r}^{2}}=\left( 3.14 \right){{\left( 2cm \right)}^{2}}=12.56c{{m}^{2}}$

Esto es importante, porque necesitamos colocar la fórmula principal:

$\displaystyle {{A}_{f}}={{A}_{0}}[1+\gamma \left( {{T}_{f}}-{{T}_{0}} \right)]$

Despejamos a la temperatura inicial

$\displaystyle {{A}_{f}}={{A}_{0}}+\gamma {{A}_{0}}\left( {{T}_{f}}-{{T}_{0}} \right)$

$\displaystyle {{A}_{f}}-{{A}_{0}}=\gamma {{A}_{0}}\left( {{T}_{f}}-{{T}_{0}} \right)$

$\displaystyle \frac{{{A}_{f}}-{{A}_{0}}}{\gamma {{A}_{0}}}={{T}_{f}}-{{T}_{0}}$

y finalmente:

$\displaystyle \frac{{{A}_{f}}-{{A}_{0}}}{\gamma {{A}_{0}}}+{{T}_{0}}={{T}_{f}}$

Invirtiendo la igualdad

$\displaystyle {{T}_{f}}=\frac{{{A}_{f}}-{{A}_{0}}}{\gamma {{A}_{0}}}+{{T}_{0}}$

Ahora podemos sustituir nuestros datos sin ningún problema:

$\displaystyle {{T}_{f}}=\frac{15c{{m}^{2}}-12.56c{{m}^{2}}}{\left( 34x{{10}^{-6}}{}^\circ {{C}^{-1}} \right)\left( 12.56c{{m}^{2}} \right)}+20{}^\circ C$