Problema 3 de Dilatación Volumétrica

Con este tercer problema de Dilatación Volumétrica o Dilatación Cúbica, el alumno finalmente refuerza el uso de la fórmula utilizando los despejes de la fórmula, ir viendo las diversas variables que se pueden obtener a través de la fórmula de dilatación superficial y que resuelve todo tipo de problemas que se puede encontrar en algún examen o tarea. 😊👇

Nivel de Dificultad: ⭐⭐⭐

Ejemplo 6. Un tanque de hierro de 300 litros de capacidad a 15°C, se llena totalmente de petróleo, si se incrementa la temperatura de ambos hasta 40°C, calcular: a) la dilatación cúbica del tanque, b) la dilatación cúbica del petróleo, c) ¿Cuánto petróleo se derramó en litros y cm³

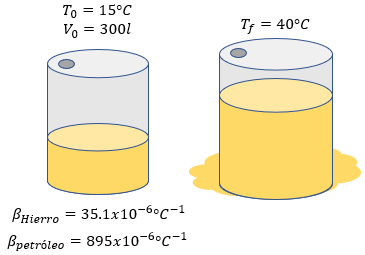
Dilatación Volumétrica Problema Ejercicio

Solución:

Si analizamos el tema de dilatación volumétrica vamos a observar como este problema es similar a uno de los expuestos en el artículo publicado. Donde también corroboramos que en la dilatación cúbica de los líquidos siempre se debe tomar en cuenta que también se calienta el recipiente que los contiene, por lo tanto se deben calcular por separado. Entonces en este ejemplo se calcularán tres cosas.

La dilatación cúbica del tanque de hierro
La dilatación cúbica del petróleo
¿Cuánto petróleo se derramó en litros y en cm³

Datos:

$\displaystyle {{V}_{0}}=300l$

$\displaystyle {{T}_{0}}=15{}^\circ C$

$\displaystyle {{T}_{f}}=40{}^\circ C$

$\displaystyle {{\beta }_{Hierro}}=35.1x{{10}^{-6}}{}^\circ {{C}^{-1}}$

$\displaystyle {{\beta }_{Petr\acute{o}leo}}=895x{{10}^{-6}}{}^\circ {{C}^{-1}}$

a) Obtener la dilatación cúbica del tanque

Para obtener la dilatación del tanque, anotamos la fórmula de dilatación volumétrica:

$\displaystyle {{V}_{f}}={{V}_{0}}[1+\beta \left( {{T}_{f}}-{{T}_{0}} \right)]$

Sustituyendo nuestros datos en la fórmula:

$\displaystyle {{V}_{f}}=300l[1+35.1x{{10}^{-6}}{}^\circ {{C}^{-1}}\left( 40{}^\circ C-15{}^\circ C \right)]$

$\displaystyle {{V}_{f}}=300l[1+35.1x{{10}^{-6}}{}^\circ {{C}^{-1}}\left( 25{}^\circ C \right)]$

Multiplicando el coeficiente de dilatación volumétrica por la temperatura:

$\displaystyle {{V}_{f}}=300l\left( 1+0.0008775 \right)$

Sumando la unidad

$\displaystyle {{V}_{f}}=300l\left( 1.0008775 \right)$

Realizando la multiplicación:

$\displaystyle {{V}_{f}}=300.26325l$

Obteniendo la dilatación cúbica del tanque:

$\displaystyle \Delta V={{V}_{f}}-{{V}_{0}}=300.26325l-300l=0.26325l$

Es decir que el tanque se dilató 0.26325 litros.

a) Obtener la dilatación cúbica del petróleo

Colocamos nuevamente la fórmula de dilatación cúbica o volumétrica:

$\displaystyle {{V}_{f}}={{V}_{0}}[1+\beta \left( {{T}_{f}}-{{T}_{0}} \right)]$

Sustituimos nuestros datos en la fórmula (recuerde que debemos anotar el coeficiente de dilatación volumétrica del petróleo)

$\displaystyle {{V}_{f}}=300l[1+895x{{10}^{-6}}{}^\circ {{C}^{-1}}\left( {{40}^{{}^\circ }}C-{{15}^{{}^\circ }}C \right)]$

$\displaystyle {{V}_{f}}=300l[1+895x{{10}^{-6}}{}^\circ {{C}^{-1}}\left( {{25}^{{}^\circ }}C \right)]$

Realizando el producto entre el coeficiente de dilatación volumétrica por la temperatura

$\displaystyle {{V}_{f}}=300l\left( 1+0.022375 \right)$

Sumando la unidad:

$\displaystyle {{V}_{f}}=300l\left( 1.022375 \right)$

Multiplicando por 300, tenemos:

$\displaystyle {{V}_{f}}=306.7125l$

Obteniendo la dilatación cúbica del petróleo

$\displaystyle \Delta V={{V}_{f}}-{{V}_{0}}=306.7125l-300l=6.7125l$

Es decir que el petróleo se dilató 6.7125 litros

c) Obtener el petróleo derramado en litros y cm³

Puesto que el tanque de hierro se dilató 0.26325 litros y el petróleo 6.7125 litros , la diferencia entre los dos volúmenes equivaldrá al petróleo derramado:

$\displaystyle 6.7125l-0.26325l=6.44925l$