Solución Problema 1 de Calor Específico

En este ejemplo de los problemas resueltos para ejercicios de práctica del tema de Calor Específico, es importante tener en cuenta el uso correcto de la fórmula, es por eso que se realizan los ejercicios paso a paso con su solución correspondiente. Recuerde que con este tipo de ejemplos el alumno podrá corroborar su respuesta y verificar si ha llegado al mismo resultado. 😊👇

Nivel de Dificultad: ⭐⭐

Problema 4.- ¿Qué cantidad de calor se necesita suministrar a 600 gramos de agua para que eleve su temperatura de 25°C a 100°C?

Capacidad Calorífica

Solución:

Este ejemplo es muy importante, porque vamos a utilizar el calor específico del agua, que debería ser un dato que todos necesitamos saber. Y lo hemos explicado en el tema de calor específico. El agua tiene una propiedad muy interesante, solo se necesita de 1 cal/g°C para elevar su temperatura. Este dato está implícita en el problema, pasemos a recoger los datos y comencemos por resolver el ejercicio.

Obtener la cantidad de calor en el agua

Datos:

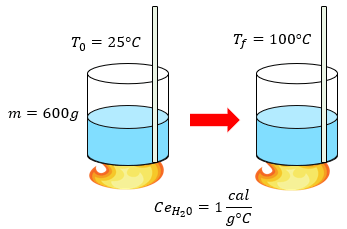
$\displaystyle m=600g$

$\displaystyle {{T}_{0}}=25{}^\circ C$

$\displaystyle {{T}_{f}}=100{}^\circ C$

$\displaystyle C{{e}_{{{H}_{2}}O}}=1\frac{cal}{{{g}^{{}^\circ }}C}$

a) Obtener la cantidad de calor en el agua

Recordemos nuestra fórmula del calor específico.

$\displaystyle {{C}_{e}}=\frac{\Delta Q}{m\Delta T}$

De esta fórmula, vamos a despejar al incremento de calor, es decir a ΔQ

$\displaystyle \Delta Q=m{{C}_{e}}\Delta T$

A la diferencia de temperatura, también la podemos colocar de esta manera:

$\displaystyle \Delta Q=m{{C}_{e}}\left( {{T}_{f}}-{{T}_{0}} \right)$

Sustituyendo nuestros datos en la fórmula, obtenemos:

$\displaystyle \Delta Q=\left( 600g \right)\left( 1\frac{cal}{g{}^\circ C} \right)\left( 100{}^\circ C-25{}^\circ C \right)$

Realizando la diferencia de temperatura:

$\displaystyle \Delta Q=\left( 600g \right)\left( 1\frac{cal}{g{}^\circ C} \right)\left( 75{}^\circ C \right)$

Multiplicando, obtenemos:

$\displaystyle \Delta Q=\left( 600g \right)\left( 1\frac{cal}{g{}^\circ C} \right)\left( 75{}^\circ C \right)=45000cal$

Un total de 45,000 calorías

Respuesta:

$\displaystyle \Delta Q=45000cal$

Deja una respuesta Cancelar la respuesta

Subir

🤓 Únete a nuestro canal de WhatsApp 👉UNIRME

+