Solución Problema 1 de Dilatación Lineal

En este ejemplo de los problemas resueltos para ejercicios de práctica del tema de Dilatación Lineal, es importante tener en cuenta el uso correcto de la fórmula, es por eso que se realizan los ejercicios paso a paso con su solución correspondiente. Recuerde que con este tipo de ejemplos el alumno podrá corroborar su respuesta y verificar si ha llegado al mismo resultado. 😊👇

Nivel de Dificultad: ⭐⭐

Problema 3. A una temperatura de 18°C una varilla de hierro tiene una longitud de 8 m. ¿Cuál será la longitud al aumentar su temperatura a 55 °C ?

Problema de Dilatación Lineal

Solución:

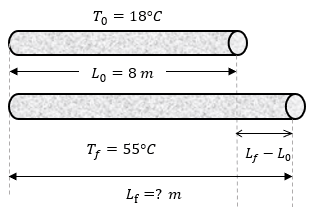
En el problema de dilatación lineal nos piden encontrar la longitud final, es decir; vamos a emplear la fórmula de dilatación para encontrar qué tanto ha aumentado la varilla de fierro cuando se somete a una diferencia de temperatura.

Obtención de la dilatación final

Datos:

$\displaystyle {{\alpha }_{Fe}}=11.7x{{10}^{-6}}{}^\circ {{C}^{-1}}$

$\displaystyle {{L}_{0}}=8m$

$\displaystyle {{T}_{0}}=18{}^\circ C$

$\displaystyle {{T}_{f}}=55{}^\circ C$

a) Obteniendo la longitud final

Para comenzar a obtener la longitud final, veamos la fórmula principal:

$\displaystyle {{L}_{f}}={{L}_{0}}[1+\alpha \left( {{T}_{f}}-{{T}_{0}} \right)]$

Sustituyendo nuestros datos en la fórmula:

$\displaystyle {{L}_{f}}=8m[1+11.7x{{10}^{-6}}{}^\circ {{C}^{-1}}\left( 55{}^\circ C-18{}^\circ C \right)]$

Haciendo la diferencia de temperatura, obtenemos:

$\displaystyle {{L}_{f}}=8m[1+11.7x{{10}^{-6}}{}^\circ {{C}^{-1}}\left( 37{}^\circ C \right)]$

Multiplicando por el coeficiente de dilatación lineal

$\displaystyle {{L}_{f}}=8m\left( 1+4.329x{{10}^{-4}} \right)$

Sumando a la unidad

$\displaystyle {{L}_{f}}=8m\left( 1.0004329 \right)$

Multiplicando por 8

$\displaystyle {{L}_{f}}=8.0034632m$

Es decir que la longitud final es de 8.0034632 metros

Pero si quisiéramos conocer lo que realmente ha aumentado por la dilatación, tendríamos que realizar.

$\displaystyle {{L}_{f}}-{{L}_{0}}=8.0034632m-8m=0.0034632m$

Esto es equivalente a 3.4632 mm (milímetros de dilatación).

Resultado:

$\displaystyle {{L}_{f}}=8.0034632m$

Deja una respuesta Cancelar la respuesta

Subir

🤓 Estamos en Whatsapp 👉Únete a nuestro canal

+