Solución Problema 1 del Principio de Arquímedes
Para perfeccionar mucho mejor el tema del principio de Arquímedes o también titulado en algunos libros de Física como Teorema de Arquímedes es de vital importancia asegurarnos de hacer uso correcto de la fórmula, así como de interpretar los problemas de la mejor manera y clara posible. Con estos ejemplos el estudiante podrá corroborar sus resultados y aumentar el autoaprendizaje. 😀
Nivel de Dificultad: ⭐⭐
Problema 3. Un cubo de cobre, de base igual a 35 cm² y una altura de 12 cm, se sumerge hasta la mitad, por medio de un alambre, en un recipiente que contiene alcohol. a) ¿Qué volumen de alcohol desaloja?, b) ¿Qué magnitud de empuje recibe? c) ¿Cuál es la magnitud del peso aparente del cubo debido al empuje, si la magnitud de su peso es de 32.36 N?
Solución:
Este problema es muy similar al problema 1, a excepción que en este problema se retoma lo del volumen desalojado que es algo que nos piden en el primer inciso, después la magnitud del empuje y finalmente una pregunta del peso aparente, comencemos con colocar nuestros datos:
- Calcular el volumen desalojado
- Calcular la magnitud del empuje que recibe el cubo
- La magnitud del peso aparente
Datos:
V = (35 cm²)(12 cm) = 420 cm³
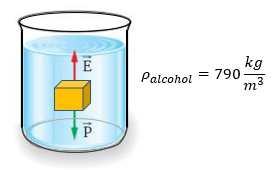
ρ(alcohol) = 790 kg/m³
p(real) = 32.36 N
a) Calculando el volumen desalojado
El volumen de líquido desalojado es igual al volumen del cubo sumergido en el alcohol. Dado que el cubo se sumerge hasta la mitad de su altura:
$\displaystyle {{h}_{{sumergida}}}=\frac{{12cm}}{2}=6cm$
$\displaystyle {{v}_{{desalojado}}}=base\times {{h}_{{sumergida}}}$
$\displaystyle {{v}_{{desalojado}}}=35c{{m}^{2}}\times 6cm$
$\displaystyle {{v}_{{desalojado}}}=210c{{m}^{3}}$
$\displaystyle {{V}_{desalojado}}={{V}_{cubo}}$
Observar que el volumen lo tenemos en centímetros cúbicos, lo convertiremos a metros cúbicos con el siguiente factor de conversión.
$\displaystyle {{V}_{desalojado}}=210c{{m}^{3}}\left( \frac{1{{m}^{3}}}{1000000c{{m}^{3}}} \right)=2.1x{{10}^{-4}}{{m}^{3}}$
Es decir que nuestro volumen desalojado es de 2.1x10^(-4) m³
b) Calculando la magnitud del empuje que recibe el cubo
Para obtener el empuje, simplemente utilizaremos la siguiente fórmula:
$\displaystyle E=\rho gV=\left( 790\frac{kg}{{{m}^{3}}} \right)\left( 9.81\frac{m}{{{s}^{2}}} \right)\left( 2.1x{{10}^{-4}}{{m}^{3}} \right)=1.628N$
Un empuje de 1.628 Newtons
c) Calcular la magnitud del peso aparente
Para obtener el peso aparente, relacionemos la siguiente fórmula:
$\displaystyle {{P}_{aparente}}={{P}_{real}}-E$
Sustituyendo nuestros datos en la fórmula:
$\displaystyle {{P}_{aparente}}=32.36N-1.628N=30.73N$
Nuestro peso aparente es de 30.73 Newtons.
Resultados:
$\displaystyle \begin{array}{*{20}{l}} {{{V}_{{desalojado}}}=2.1x{{{10}}^{{-4}}}{{m}^{3}}} \\ {E=1.628N} \\ {{{P}_{{aparente}}}=30.73N} \end{array}$
-
Fran dice:
Me pueden ayudar con este problema que todavia no logro plantearlo, dice asi:
Calcular la fuerza ascensional que recibe un globo de 5 m de radio y pesa 540 kgf (densidad del aire 1,29kg/m3) -
Blanca Stephany dice:
Quiero ayuda con mis ejercicios de tarea
Que es sobre un cubo de 0.125m3 de volumen se sumeje en agua =1000 kg sobre m3 calcula el empuje que recibe? -
Victor dice:
Pero en el problema dice que solo se sumerge la mitad del cubo, la otra mitad queda fuera del líquido.
Y el resultado da como si se hubiera sumergido todo el cubo. -
renato dice:
Cordial y respetuoso saludo.
Quiero hacer una observación respetuosa a manera de pregunta: Si la esfera de cobre solo entra al alcohol hasta la mitad,¿no era tomar la mitad del volumen que equivale al volumen de alcohol que desaloja?
Deja una respuesta
un cubo de cobre de base 35m2 y una altura de 12cm se sumerge asta la mitad por medio de un alambre en un resipiente con alcohol