Solución Problema 2 de Caída Libre

De forma similar al ejemplo anterior, en este problema de Caída Libre , debemos reforzar el concepto principal que es la utilización correcta de la fórmula, no olvide que con estos ejercicios se proporciona la solución paso a paso del ejemplo y nuevamente el alumno comprueba sus resultados de manera correcta y concisa. 😊👇

Nivel de Dificultad: ⭐⭐

Solución:

Al igual que el problema 4, este problema es muy sencillo de resolver porque contamos con los datos necesarios para resolver tanto la altura del edificio, como la magnitud de la velocidad final. Para ello primero recopilaremos nuestros datos y empezamos a resolver.

• Calcular la altura del edificio
• Obtener la magnitud de la velocidad final

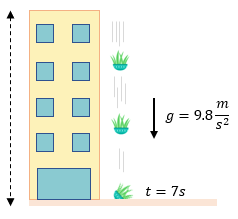
Datos:

$\displaystyle t=7s$

$\displaystyle g=9.8\frac{m}{{{s}^{2}}}$

a) Obtener la altura del edificio

Para que podamos calcular la altura, emplearemos la siguiente fórmula:

$\displaystyle h={{v}_{0}}t+\frac{g{{t}^{2}}}{2}$

Recordemos que al ser una caída libre, la velocidad inicial es cero. Por lo que la fórmula finalmente se verá reducida:

$\displaystyle h=\frac{g{{t}^{2}}}{2}$

Ahora solamente sustituimos nuestros datos en la fórmula.

$\displaystyle h=\frac{g{{t}^{2}}}{2}=\frac{\left( 9.8\frac{m}{{{s}^{2}}} \right){{\left( 7s \right)}^{2}}}{2}=\frac{\left( 9.8\frac{m}{{{s}^{2}}} \right)\left( 49{{s}^{2}} \right)}{2}=\frac{480.2m}{2}=240.1m$

Es decir que la altura de nuestro edificio es de 240.1 metros

b) Obtener la magnitud de la velocidad final

Para poder obtener la magnitud de la velocidad final, tendremos que recurrir a la siguiente fórmula:

$\displaystyle {{v}_{f}}={{v}_{0}}+gt$

Recordar, que como no hay velocidad inicial por ser caída libre, entonces la fórmula se reduce:

$\displaystyle {{v}_{f}}=gt$

Sustituyendo nuestros datos en la fórmula:

$\displaystyle {{v}_{f}}=gt=\left( 9.8\frac{m}{{{s}^{2}}} \right)\left( 7s \right)=68.6\frac{m}{s}$

Por lo que la velocidad final es de 68.6 m/s

Resultados:

$\displaystyle \begin{array}{l}h=240.1m\\{{v}_{f}}=68.9\frac{m}{s}\end{array}$