Solución Problema 2 de Calor Específico

De forma similar al ejemplo anterior, en este problema de Calor Específico , debemos reforzar el concepto principal que es la utilización correcta de la fórmula, con este ejercicio lo terminará de comprender, no olvide que con estos ejercicios se proporciona la solución paso a paso del ejemplo y nuevamente el alumno comprueba sus resultados de manera correcta y concisa. 😊👇

Nivel de Dificultad: ⭐⭐

Problema 5.- ¿Cuántas calorías se deben suministrar para que un pedazo de metal de hierro de 3.5kg eleve su temperatura de 26°C a 140°C?

Calor Específico problema 2

Solución:

Este problema es muy similar al ejemplo anterior, con la diferencia de que en este ejercicio, no se trata del calor específico del agua, sino del calor específico del hierro. Para poder resolver el problema, hacemos el mismo procedimiento anterior, tanto en el despeje como en la sustitución de los datos en la fórmula.

Obtener las calorías para suministrar un pedazo de metal

Datos:

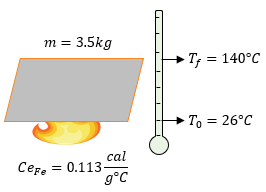
$\displaystyle m=3.5kg\left( \frac{1000g}{1kg} \right)=3500g$

$\displaystyle {{T}_{f}}=140{}^\circ C$

$\displaystyle {{T}_{0}}=26{}^\circ C$

$\displaystyle C{{e}_{Fe}}=0.113\frac{cal}{{{g}^{{}^\circ }}C}$

a) Obtener las calorías

Recordemos nuestra fórmula de calor específico

$\displaystyle Ce=\frac{\Delta Q}{m\Delta T}$

Despejando a ΔQ

$\displaystyle \Delta Q=mCe\Delta T$

Qué también la podemos escribir de la siguiente forma:

$\displaystyle \Delta Q=mCe\left( {{T}_{f}}-{{T}_{0}} \right)$

Sustituyendo nuestros valores de los datos en la fórmula:

$\displaystyle \Delta Q=mCe\Delta T=\left( 3500kg \right)\left( 0.113\frac{cal}{g{}^\circ C} \right)\left( 140{}^\circ C-26{}^\circ C \right)$

Realizando la diferencia de temperaturas:

$\displaystyle \Delta Q=mCe\Delta T=\left( 3500kg \right)\left( 0.113\frac{cal}{g{}^\circ C} \right)\left( 114{}^\circ C \right)$

Realizando las multiplicaciones.

$\displaystyle \Delta Q=mCe\Delta T=\left( 3500kg \right)\left( 0.113\frac{cal}{g{}^\circ C} \right)\left( 114{}^\circ C \right)=45087cal$

Por lo que obtenemos un valor de 45,087 calorías.

Respuesta:

$\displaystyle \Delta Q=45087ca$

Deja una respuesta Cancelar la respuesta

Subir

🤓 Únete a nuestro canal de WhatsApp 👉UNIRME

+