Solución Problema 2 de Campo Eléctrico

De forma similar al ejemplo anterior, en este problema de Campo Eléctrico, debemos reforzar el concepto principal que es la utilización correcta de la fórmula, recuerde que hay dos formas de expresar la fórmula, una en términos de la carga y otras involucrando a la distancia, con este ejercicio lo terminará de comprender, no olvide que con estos ejercicios se proporciona la solución paso a paso del ejemplo y nuevamente el alumno comprueba sus resultados de manera correcta y concisa. 😊👇

Nivel de Dificultad: ⭐⭐

Problema 6.- La intensidad del campo eléctrico producido por una carga de 8μC en un punto determinado tiene una magnitud de 4x10^(6) N/C ¿A qué distancia del punto considerado se encuentra la carga?

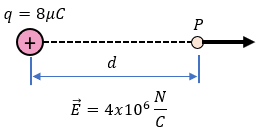
Problema de Campo Eléctrico 2

Solución:

En este problema usaremos la segunda fórmula que hemos obtenido de la intensidad de campo eléctrico, en esta fórmula empleamos un despeje de la fórmula principal para poder obtener la distancia en términos del campo eléctrico y la carga. ¿Cómo lo hacemos?, primero debemos considerar nuestros datos, veamos!

Obtener la distancia del punto donde se encuentra la carga

Datos:

$\displaystyle q=8x{{10}^{-6}}C$

$\displaystyle E=4x{{10}^{6}}\frac{N}{C}$

a) Obteniendo al distancia del punto donde está la carga

Recordemos qué la fórmula de la intensidad de campo eléctrico donde empleamos la distancia, es la siguiente:

$\displaystyle E=\frac{Kq}{{{d}^{2}}}$

Aunque lo que buscamos es la distancia, por lo tanto la vamos a despejar de esa fórmula:

$\displaystyle {{d}^{2}}=\frac{Kq}{E}$

Para quitar el cuadrado, simplemente sacamos raíz cuadrada en ambos miembros y listo.

$\displaystyle d=\sqrt{\frac{Kq}{E}}$

Ahora si podemos emplear la fórmula y sustituir nuestros datos, para ello tenemos:

$\displaystyle d=\sqrt{\frac{\left( 9x{{10}^{9}}\frac{N{{m}^{2}}}{{{C}^{2}}} \right)\left( 8x{{10}^{-6}}C \right)}{4x{{10}^{6}}\frac{N}{C}}}=\sqrt{0.018{{m}^{2}}}$

Y el resultado de la raíz cuadrada es:

$\displaystyle d=\sqrt{0.018{{m}^{2}}}=0.134m$

Es decir que la carga se encuentra a 0.134 metros

Esta cantidad en centímetros es igual a

$\displaystyle d=13.4cm$

Resultado:

$\displaystyle d=0.134m$

Deja una respuesta Cancelar la respuesta