Solución problema 2 de Capacitancia

Este es el segundo ejemplo de capacitancia que tendrás que resolver para verificar el resultado, si ya has resuelto el problema o tienes dudas de la solución, aquí la hemos realizado por ti, así que sin más preámbulos veamos la solución. 👇

Nivel de Dificultad: ⭐⭐

Problema 4 - Las placas paralelas de un capacitor con vacío están separadas una distancia de 6 mm y tienen 0.03m² de área. Se aplica una diferencia de potencial de 220 Volts a través del capacitor. Calcule a) La capacitancia, b) la carga en cada placa.

Solución problema 2 de capacitancia

Solución:

Este es un problema que implica la utilización de las dos fórmulas que conocemos hasta ahora de capacitancia, la primera fórmula esencial es la que define a la capacitancia en términos de la carga eléctrica y voltaje (Q/V) y la otra fórmula es la que hemos venido usando con el problema número 3, que implica el uso de la permitividad, área y distancia.

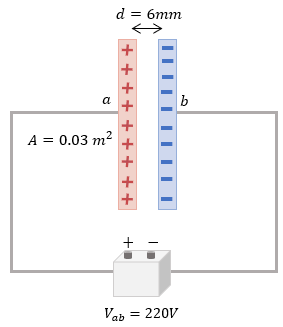
Entonces, pasamos a resolver el problema, no sin antes colocar los datos con los que contamos:

$\displaystyle d=6mm=0.006m$

$\displaystyle A=0.03{{m}^{2}}$

$\displaystyle V=220V$

$\displaystyle \varepsilon =8.85x{{10}^{{-12}}}\frac{F}{m}$

A ) Calculamos la capacitancia

Si sabemos que las placas están en el vacío, entonces la permitividad del vacío será el valor de la permitividad total. Por lo que solamente necesitamos recurrir a la fórmula de capacitancia.

$\displaystyle C=\varepsilon \frac{A}{d}$

Sustituyendo

$\displaystyle C=\left( {8.85x{{{10}}^{{-12}}}\frac{F}{m}} \right)\frac{{\left( {0.03{{m}^{2}}} \right)}}{{0.006m}}=\frac{{2.655x{{{10}}^{{-13}}}}}{{0.006m}}$