Solución Problema 2 de Dilatación Lineal

De forma similar al ejemplo anterior, en este problema de Dilatación Lineal reforzamos el concepto principal que es la utilización correcta de la fórmula, con ello se proporciona la solución paso a paso del ejemplo y nuevamente el alumno comprueba sus resultados de manera correcta y concisa. 😊👇

Nivel de Dificultad: ⭐⭐

Problema 4. ¿Cuál es la longitud de un cable de cobre al disminuir la temperatura a 12 °C, si con una temperatura de 40°C mide 430 m?

Problema de Dilatación Lineal

Solución:

En este problema veremos algo muy curioso respecto a la dilatación, ya que la dilatación no siempre se trata de "aumentar de tamaño" sino que también puede significar una "disminución de tamaño" y en este ejemplo que realizaremos se podrá observar como el metal se contrae, en vez de aumentar.

Obtención de la longitud debida a la dilatación lineal

Datos:

$\displaystyle {{\alpha }_{Cu}}=16.7x{{10}^{-6}}{}^\circ {{C}^{-1}}$

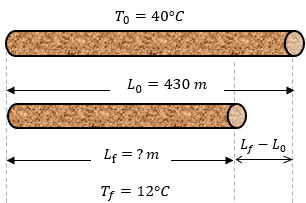
$\displaystyle {{L}_{0}}=430m$

$\displaystyle {{T}_{0}}=40{}^\circ C$

$\displaystyle {{T}_{f}}=12{}^\circ C$

a) Obteniendo la longitud final

Para comenzar a obtener la longitud final, veamos la fórmula principal:

$\displaystyle {{L}_{f}}={{L}_{0}}[1+\alpha \left( {{T}_{f}}-{{T}_{0}} \right)]$

Sustituyendo nuestros datos en la fórmula:

$\displaystyle {{L}_{f}}=430m[1+16.7x{{10}^{-6}}^{{}^\circ }{{C}^{-1}}\left( {{12}^{{}^\circ }}C-{{40}^{{}^\circ }}C \right)]$

Haciendo la diferencia de temperatura, obtenemos:

$\displaystyle {{L}_{f}}=430m[1+16.7x{{10}^{-6}}^{{}^\circ }{{C}^{-1}}\left( -{{28}^{{}^\circ }}C \right)]$

Multiplicando por el coeficiente de dilatación lineal

$\displaystyle {{L}_{f}}=430m[1-0.0004676]$

Restando la unidad

$\displaystyle {{L}_{f}}=430m(0.9995324)$

Multiplicando por 430

$\displaystyle {{L}_{f}}=429.798932m$

Hemos conservado todos los dígitos sin redondear, y obtenemos una longitud final de 429.798932 metros

Pero si quisiéramos conocer lo que realmente se ha contraído por la dilatación, tendríamos que realizar.

$\displaystyle {{L}_{f}}-{{L}_{0}}=429.798932m-430m=-0.201068m$

Es decir que se contrajo 0.201068 metros

Resultado:

$\displaystyle {{L}_{f}}=429.798932m$

Deja una respuesta Cancelar la respuesta

Subir

🤓 Únete a nuestro canal de WhatsApp 👉UNIRME

+