Solución Problema 2 de Movimiento Circular
De forma similar al ejemplo anterior, en este problema de Movimiento Circular Uniformemente Acelerado reforzamos el concepto principal que es la utilización correcta de la fórmula, con ello se proporciona la solución paso a paso del ejemplo y nuevamente el alumno comprueba sus resultados de manera correcta y concisa. 😊👇
Nivel de Dificultad: ⭐⭐⭐
Problema 7.- Una rueda de bicicleta gira con una magnitud de velocidad angular inicial de 23.4 rad/s experimentando una aceleración angular cuya magnitud es de 6 rad/s² que dura 11 segundos, calcular: a) ¿Qué magnitud de desplazamiento angular tiene a los 11 segundos?, b) ¿Qué magnitud de velocidad angular lleva a los 11 segundos?
Solución:
Al igual que el ejemplo anterior, la solución de este problema es muy sencillo. Puesto que contamos con todos los datos suficientes para emplear las fórmulas que hemos visto en el tema de movimiento circular. Para ello empecemos por recabar los datos que tenemos:
- Obtener el desplazamiento angular a los 11 segundos
- Magnitud de la velocidad angular a los 11 segundos
Datos:
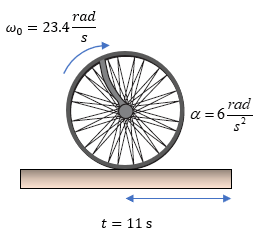
$\displaystyle {{\omega }_{0}}=23.4\frac{rad}{s}$
$\displaystyle \alpha =6\frac{rad}{{{s}^{2}}}$
$\displaystyle t=11s$
a) Obteniendo el desplazamiento angular a los 11 segundos
Para poder obtener el desplazamiento angular a los 11 segundos, basta con aplicar la fórmula del desplazamiento en términos del tiempo.
$\displaystyle \theta ={{\omega }_{0}}t+\frac{\alpha {{t}^{2}}}{2}$
Sustituyendo nuestros datos en la fórmula del desplazamiento angular:
$\displaystyle \theta =\left( 23.4\frac{rad}{s} \right)\left( 11s \right)+\frac{\left( 6\frac{rad}{{{s}^{2}}} \right){{\left( 11s \right)}^{2}}}{2}$
$\displaystyle \theta =257rad+\frac{\left( 6\frac{rad}{{{s}^{2}}} \right)121{{s}^{2}}}{2}$
$\displaystyle \theta =257rad+\frac{726rad}{2}$
Esto nos da:
$\displaystyle \theta =257rad+363rad=620rad$
Por lo que el desplazamiento angular es de 620 radianes
b) Obteniendo la magnitud de la velocidad angular a los 11 segundos
Para obtener este inciso, podemos aplicar la fórmula de la velocidad angular final:
$\displaystyle {{\omega }_{f}}={{\omega }_{0}}+\alpha t$
Ahora sustituimos nuestros datos en la fórmula:
$\displaystyle {{\omega }_{f}}=23.4\frac{rad}{s}+\left( 6\frac{rad}{{{s}^{2}}} \right)\left( 11s \right)$
$\displaystyle {{\omega }_{f}}=23.4\frac{rad}{s}+66\frac{rad}{s}$
Sumando
$\displaystyle {{\omega }_{f}}=89.4\frac{rad}{s}$
Por lo que obtenemos una velocidad angular de 89.4 rad/s
Resultado:
$\displaystyle \begin{array}{l}\theta =620rad\\{{\omega }_{f}}=89.4\frac{rad}{s}\end{array}$
Deja una respuesta