Solución Problema 2 del Principio de Arquímedes

En este segundo problema, nuevamente es con la intensión de perfeccionar mucho mejor el tema del principio de Arquímedes o también titulado en algunos libros de Física como Teorema de Arquímedes es de vital importancia asegurarnos de hacer uso correcto de la fórmula, así como de interpretar los problemas de la mejor manera y clara posible. Con estos ejemplos el estudiante podrá corroborar sus resultados y aumentar el autoaprendizaje. 😀

Nivel de Dificultad: ⭐⭐

Problema 4. Durante un experimento, un cubo de madera de arista de 1 metro, se coloca en un recipiente que contiene agua. Se notó que el cubo flotó con el 60% de su volumen sumergido. a) Calcule la intensidad del empuje ejercido por el agua sobre el bloque de madera, b) Calcule la intensidad de fuerza vertical "F", que debe actuar sobre el bloque, para que permanezca totalmente sumergido.

Problema de Arquimedes Flotación Solución:

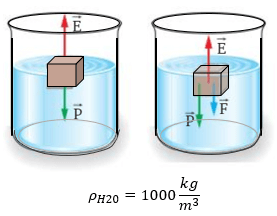
En este problema podemos apreciar que se involucra un término de porcentajes, es decir; nos dice el problema que el cubo flotó solo con el 60% de su volumen, entonces en nuestro cálculo esto tendrá ciertas modificaciones, basado en este dato importante tendremos que realizar su solución.

Calcular la intensidad del empuje
Calcular la fuerza vertical F, para que el bloque esté totalmente sumergido.

Datos:

V = (1m)(1m)(1m) = 1m³ (Porque la arista vale 1 metro, entonces el volumen será de 1 metro cúbico).

ρ(H20) = 1000 kg/m³

a) Calculando la intensidad del empuje

Para calcular la intensidad del empuje, necesitamos saber el volumen desalojado, pero dicho volumen desalojado nos dice que solamente el 60% del cubo está sumergido. Entonces decimos:

$\displaystyle {{V}_{desalojado}}=\left( 1{{m}^{3}} \right)\left( 0.6 \right)=0.6{{m}^{3}}$

Es decir que solo hay 0.6 metros cúbicos de volumen desalojado. Ahora si podemos calcular el empuje.

$\displaystyle E={{\rho }_{{{h}_{2}}o}}{{V}_{desalojado}}g$

Sustituyendo nuestros datos en la fórmula:

$\displaystyle E=(1000\frac{kg}{{{m}^{3}}})(0.6{{m}^{3}})(9.8\frac{m}{{{s}^{2}}})=5880N$

Un empuje de 5880 Newtons

b) Calcular la fuerza vertical "F" para que el bloque esté totalmente sumergido

Para poder saber este dato, debemos saber que el bloque inicialmente estuvo sumergido solo el 60%, es decir que faltaba el 40% para que todo el cubo estuviera sumergido. Entonces debemos comprender que existe una fuerza "F" que jala hacía abajo necesaria para sumergir por completo al cubo.

Si calculamos nuevamente el volumen que desalojaría ese 40% restante, lo haríamos de la siguiente forma:

$\displaystyle {{V}_{restante}}=\left( 1{{m}^{3}} \right)\left( 0.4 \right)=0.4{{m}^{3}}$

Bien, ahora calcularíamos nuevamente el empuje (qué sería la fuerza "F") para encontrar cuánto era necesario aplicar de empuje para que el cubo estuviera sumergido totalmente.

$\displaystyle E'=F=(1000\frac{kg}{{{m}^{3}}})(0.4{{m}^{3}})(9.8\frac{m}{{{s}^{2}}})=3920N$

Ahora sabemos que la fuerza vertical necesaria para sumergir al bloque por completa, era de 3920 Newtons.

Resultados:

$\displaystyle \begin{array}{l}E=5880N\\E'=F=3920N\end{array}$

2 Comentarios Publicados

Reynaldo dice:

27 abril, 2023 a las 11:20 am

Muy claro el desarrollo de este tema, excelente.

Responder
MARISOL dice:

3 abril, 2024 a las 1:29 pm

gracias

Responder

Deja una respuesta Cancelar la respuesta