Solución Problema 3 de Caída Libre

Con este tercer problema de Caída Libre, el alumno finalmente refuerza el uso de la fórmula utilizando los despejes de la fórmula, ir viendo las diversas variables que se pueden obtener a través de la caída libre y que resuelve todo tipo de problemas que se puede encontrar en algún examen o tarea. 😊👇

Nivel de Dificultad: ⭐⭐⭐

Solución:

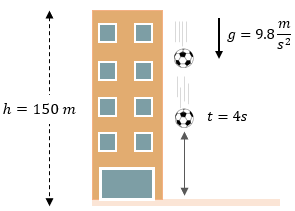
Este problema implican más casos para resolver así como también el uso de otras fórmulas que podemos hacer uso en el tema de caída libre, si leemos nuevamente nuestro ejercicio, vamos a darnos cuenta que solamente contamos con una altura de 150 metros desde donde se deja caer libremente una pelota. Para proceder a resolver, recogemos los datos.

• Distancia descendida a los 4 segundos
• ¿Qué velocidad tiene a los 4 segundos?
• ¿Distancia que le falta recorrer para llegar al suelo?

Datos:

$\displaystyle h=150m$

$\displaystyle g=9.8\frac{m}{{{s}^{2}}}$

a) Obtener la distancia a los 4 segundos cuando desciende la pelota

Para poder obtener la distancia que recorre a los 4 segundos, podemos utilizar la siguiente fórmula:

$\displaystyle h={{v}_{0}}t+\frac{g{{t}^{2}}}{2}$

Recordar, que como es una caída libre, la velocidad inicial es nula, o sea cero. Por lo que la fórmula se reduce:

$\displaystyle h=\frac{g{{t}^{2}}}{2}$

Vamos a colocar los 4 segundos en la "t" de tiempo. De esta forma:

$\displaystyle h=\frac{g{{t}^{2}}}{2}=\frac{\left( 9.8\frac{m}{{{s}^{2}}} \right){{\left( 4s \right)}^{2}}}{2}$

Realizando las operaciones indicadas:

$\displaystyle h=\frac{g{{t}^{2}}}{2}=\frac{\left( 9.8\frac{m}{{{s}^{2}}} \right)16{{s}^{2}}}{2}=\frac{156.8m}{2}=78.4m$

Es decir que la altura a los 4 segundos es de 78.4 metros

b) ¿Qué velocidad tendrá a los 4 segundos?

Para la velocidad a los 4 segundos, usamos la siguiente fórmula:

$\displaystyle {{v}_{f}}={{v}_{0}}+gt$

Recordar, que como no hay velocidad inicial por ser caída libre, entonces la fórmula se reduce:

$\displaystyle {{v}_{f}}=gt$

Sustituyendo nuestros datos y calculando:

$\displaystyle {{v}_{f}}=gt=\left( 9.8\frac{m}{{{s}^{2}}} \right)\left( 4s \right)=39.2\frac{m}{s}$

Por lo que la velocidad a los 4 segundos es de 39.2 m/s

c) Distancia que le falta para llegar al suelo

Aunque parezca difícil resolver este inciso, no lo es. Es muy fácil, recordemos que a los 4 segundos ha recorrido 78.4 metros y que la altura desde donde se dejó caer la pelota es de 150 metros, entonces la diferencia es la cantidad que falta para llegar al suelo, es decir:

$\displaystyle {{h}_{T}}={{h}_{1}}+{{h}_{2}}$

Es como si tuviéramos:

$\displaystyle 150=78.4+{{h}_{2}}$

Despejando "h2" qué sería la distancia que falta para llegar al suelo.

$\displaystyle {{h}_{2}}=150-78.4=71.6m$

Es decir que nos hace falta recorrer 71.6 metros para llegar al suelo.

Resultado:

$\displaystyle \begin{array}{l}h=78.4m\\{{v}_{f}}=39.2\frac{m}{s}\\{{h}_{2}}=71.6m\end{array}$