Solución Problema 3 de Capacitancia

Con este último problema de Capacitores o Condensadores, el alumno finalmente refuerza el uso de la fórmula utilizando los despejes de la fórmula, ir viendo las diversas variables que se pueden obtener a través de la fórmula de la capacitancia y que resuelve todo tipo de problemas que se puede encontrar en algún examen o tarea. 😊👇

Nivel de Dificultad: ⭐⭐

Problema 5.- Dos láminas cuadradas de estaño de 11 cm de lado están adheridas a las caras opuestas de una lámina de vidrio de 0.09 mm de espesor con una permitividad relativa εr = 4.7 ¿cuál será su capacitancia?.

Ejercicio de Capacitancia

Solución:

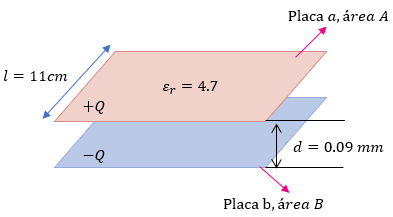
Si observamos este ejercicio, es muy similar al problema 2, solo que si analizamos bien, vemos que no se trata de una lámina de mica, sino que es una lámina de vidrio. Por lo tanto la permitividad será diferente, entonces debemos recoger los datos y pasar las unidades a metros tanto de la distancia entre las placas, así como del tamaño de las láminas.

Obtener la capacitancia

Datos:

$\displaystyle l=11cm\left( \frac{1m}{100cm} \right)=0.11m$

$\displaystyle d=0.09mm\left( \frac{1m}{1000mm} \right)=9x{{10}^{-5}}m$

$\displaystyle {{\varepsilon }_{r}}=4.7$

$\displaystyle {{\varepsilon }_{0}}=8.85x{{10}^{-12}}\frac{F}{m}$

a) Obtener la capacitancia

Primero comenzamos con calcular la permitividad de la lámina de vidrio.

$\displaystyle \varepsilon ={{\varepsilon }_{0}}{{\varepsilon }_{r}}$

Ahora sustituimos los datos en la fórmula:

$\displaystyle \varepsilon ={{\varepsilon }_{0}}{{\varepsilon }_{r}}=\left( 8.85x{{10}^{-12}}\frac{F}{m} \right)\left( 4.7 \right)=41.595x{{10}^{-12}}\frac{F}{m}$

Ahora es momento de calcular el área de las placas

$\displaystyle A={{l}^{2}}={{\left( 0.11m \right)}^{2}}=0.0121{{m}^{2}}$

Ahora se sustituyen los datos en la fórmula de la capacitancia.

$\displaystyle C=\varepsilon \frac{A}{d}$

Sustituyendo nuestros datos en la fórmula:

$\displaystyle C=\varepsilon \frac{A}{d}=\left( 41.595x{{10}^{-12}}\frac{F}{m} \right)\left( \frac{0.0121{{m}^{2}}}{9x{{10}^{-5}}m} \right)=5.59x{{10}^{-9}}F$

Tenemos un valor de 5.59 nF

Respuesta:

$\displaystyle C=5.59x{{10}^{-9}}F$

2 Comentarios Publicados

César dice:

9 noviembre, 2023 a las 10:10 am

Hola.Realicé con una calculadora esto y me muestra :
4.1595x10^-10 en la parte de la solución donde dice:
«Ahora sustituimos los datos de la fórmula» y además donde dice «Sustituyendo nuestros datos en la fórmula» a lo cual me muestra la calculadora científica otro resultado. ¿Puede ayudarme?

Responder
1. Carlos julián dice:
  
  11 noviembre, 2023 a las 10:34 am
  
  César revisa tu calculadora, nuestra operación está bien. Tienes error en una potencia de 10.
  
  Responder

Deja una respuesta Cancelar la respuesta