Solución Problema 3 de la Ley de Boyle - Mariotte

Con este tercer problema de La Ley de Boyle - Mariotte el alumno finalmente refuerza el uso de la fórmula utilizando los diversos despejes de la fórmula, ir viendo las diversas variables que se pueden obtener a través de la fórmula de la ley de Boyle-Mariotte y que resuelve todo tipo de problemas que se puede encontrar en algún examen o tarea. 😊👇

ivel de Dificultad: ⭐⭐

Solución:

Nuevamente este tipo de problema es un ejercicio muy fácil de resolver, pues nos proporcionan las condiciones iniciales tanto de la presión como del volumen, y sabemos nosotros que esto ocurre cuando la temperatura se mantiene constante (Esto es por la ley de Boyle - Mariotte), o también conocido como proceso isotérmico. Basándonos en los datos del problema, entonces pasemos a resolver el ejercicio.

• Obtener la presión final del gas

Datos:

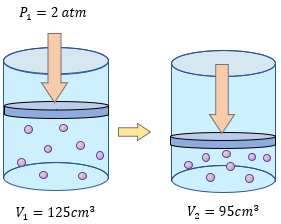
$latex \displaystyle {{P}_{1}}=2atm$

$latex \displaystyle {{V}_{1}}=125c{{m}^{3}}$

$latex \displaystyle {{V}_{2}}=95c{{m}^{3}}$

a) Obtener la presión final del gas

Recordemos que nuestra ley de Boyle - Mariotte tiene por fórmula la siguiente igualdad:

$latex \displaystyle {{P}_{1}}{{V}_{1}}={{P}_{2}}{{V}_{2}}$

Como la incógnita es la presión final P2, entonces despejamos:

$latex \displaystyle {{P}_{2}}=\frac{{{P}_{1}}{{V}_{1}}}{{{V}_{2}}}$

Ahora sustituimos nuestros datos en la fórmula.

$latex \displaystyle {{P}_{2}}=\frac{{{P}_{1}}{{V}_{1}}}{{{V}_{2}}}=\frac{\left( 2atm \right)\left( 125c{{m}^{3}} \right)}{95c{{m}^{3}}}=2.63atm$

Es decir que ahora tenemos 2.63 atmósferas de presión final

Resultado:

$latex \displaystyle {{P}_{2}}=2.63atm$