Solución Problema 3 de La Ley de los Gases Ideales

Con este tercer problema de Ley de los gases ideales o gases perfectos, el alumno finalmente refuerza el uso de la fórmula utilizando los despejes de la fórmula, ir viendo las diversas variables que se pueden obtener a través de la fórmula de los gases, en este ejemplo se acompaña con la ley de Boyle - Mariotte , recuerde practicar este tipo de problemas que se puede encontrar en algún examen o tarea. 😊👇

Nivel de Dificultad: ⭐⭐⭐

Problema 5.- En un laboratorio, hay una cantidad de 20 mols de un gas perfecto que sufre expansión isotérmica. La presión inicial de esta masa de gas es de 10 atm y el volumen 8 litros. Al final de la expansión, el volumen es de 40 L. Por lo tanto, determine. a) La presión final de la masa de gas, b) la temperatura que se produce en la transformación

Ley de los gases ideales ejercicios

Solución:

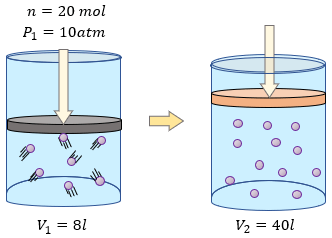
Aunque el problema parezca similar a los dos anteriores, este problema no es así, pues prácticamente tenemos más datos de lo normal, esto indica que el problema primero tiene que analizarse completamente para darle una solución razonable. Si analizamos nos dice que en condiciones iniciales la presión es de 10 atm y el volumen de 8 litros, después de la expansión el volumen incrementa a 40 litros pero se desconoce la presión, y finalmente nos piden la temperatura que se produce en esa expansión isotérmica.

Obtener la presión final de la masa de gas
Obtener la temperatura que se produce en la transformación

Datos:

$\displaystyle n=20mol$

$\displaystyle {{P}_{1}}=10atm$

$\displaystyle {{V}_{1}}=8l$

$\displaystyle {{V}_{2}}=40l$

$\displaystyle R=0.0821\frac{atm\cdot l}{mol\cdot K}$

a) Obtener la presión final de la masa de gas

Para saber la presión final, debemos recordar el tema de la Ley de Boyle Mariotte ya que ahí se analiza las condiciones iniciales y finales después de un aumento de presión o volumen, y su fórmula es:

$\displaystyle {{P}_{1}}{{V}_{1}}={{P}_{2}}{{V}_{2}}$

Si, despejamos a "P2" porque es la presión final, obtenemos:

$\displaystyle {{P}_{2}}=\frac{{{P}_{1}}{{V}_{1}}}{{{V}_{2}}}$

Sustituyendo los datos en la fórmula:

$\displaystyle {{P}_{2}}=\frac{{{P}_{1}}{{V}_{1}}}{{{V}_{2}}}=\frac{\left( 10atm \right)\left( 8l \right)}{40l}=\frac{80atm\cdot l}{40l}=2atm$

Por lo que la presión disminuyó a solo 2 atmósferas.

¡Muy bien!, ahora tenemos que calcular el siguiente inciso.

b) Obtener la temperatura que se produce en la expansión

Para este caso, tendremos que usar las condiciones finales, es lógico ya que todo sucedió después de la expansión. Entonces planteamos la ecuación de los gases ideales:

$\displaystyle PV=nRT$

Despejamos a la temperatura "T"

$\displaystyle T=\frac{PV}{nR}$

Usaremos la presión de 2 atmósferas y el volumen de 40 litros

$\displaystyle T=\frac{PV}{nR}=\frac{\left( 2atm \right)\left( 40l \right)}{\left( 20mol \right)\left( 0.0821\frac{atm\cdot l}{mol\cdot K} \right)}=\frac{80atm\cdot l}{1.642\frac{atm\cdot l}{K}}=48.7K$

Es decir que la temperatura final fue de 48.7 K

Resultados:

$\displaystyle \begin{array}{l}{{P}_{2}}=2atm\\T=48.7K\end{array}$

2 Comentarios Publicados

ROLANDO CASTILLO DURAND dice:

20 marzo, 2023 a las 7:32 pm

Excelentes ejercicios, muy bien explicados
felicidades

Responder
Edgar dice:

7 agosto, 2023 a las 10:27 am

Ejercicios muy buenos, claros y puntuales.........espero que sigan haciendo mas ejercicios para pensar

Responder

Deja una respuesta Cancelar la respuesta