Solución Problema 3 de Movimiento Circular
Con este tercer problema de Movimiento Circular Uniformemente Acelerado, el alumno finalmente refuerza el uso de la fórmula utilizando los despejes de la fórmula, ir viendo las diversas variables que se pueden obtener a través del MCUA para aprender a resolver cualquier tipo de problemas que se puede encontrar en algún examen o tarea. 😊👇
Nivel de Dificultad: ⭐⭐
Problema 8.- Determinar la velocidad lineal o tangencial de una partícula que tiene una velocidad angular cuya magnitud es de 71 rad/s y su radio de giro es de 0.8 metros
Solución:
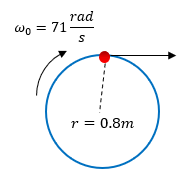
Cuando se analiza el problema, es fácil de captar y comprender lo que pide, ya que es un cálculo muy sencillo. La velocidad lineal o velocidad tangencial es aquella velocidad que es producto de la velocidad angular por el radio de la circunferencia. Entonces, recojamos los datos que tenemos:
- Obtener la velocidad lineal o tangencial
Datos:
$\displaystyle \omega =71\frac{rad}{s}$
$\displaystyle r=0.8m$
a) Obteniendo la velocidad lineal o tangencial
La fórmula de la velocidad lineal o tangencial es la siguiente:
$\displaystyle {{v}_{t}}=\omega t$
Sustituyendo nuestros datos en la fórmula, obtenemos:
$\displaystyle {{v}_{t}}=\omega t=\left( 71\frac{rad}{s} \right)\left( 0.8m \right)=56.8\frac{m}{s}$
Nuestra velocidad lineal es de 56.8 m/s
Resultado:
$\displaystyle {{v}_{t}}=56.8\frac{m}{s}$
Deja una respuesta