Solución Problema 3 de Teorema de Torricelli

Con este tercer problema del Teorema de Torricelli, el alumno finalmente refuerza el uso de la fórmula utilizando los despejes de la fórmula, ir viendo las diversas variables que se pueden obtener a través de la fórmula del teorema de torricelli, que resuelve todo tipo de problemas que se puede encontrar en algún examen o tarea. 😊👇

Nivel de Dificultad: ⭐⭐⭐

Ejemplo 5. Logre determinar a qué altura se debe abrir un orificio de un tanque de gasolina, para que el líquido salga con una velocidad de 13.5 m/s

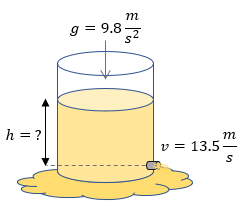
Teorema de Torricelli Problemas

Solución:

En este problema vamos a realizar un despeje de la fórmula principal, puesto que la altura no está de manera directa. El problema es muy fácil de resolver.

Obtener la altura del orificio

Datos:

$\displaystyle v=13.5\frac{m}{s}$

$\displaystyle g=9.8\frac{m}{{{s}^{2}}}$

a) Obteniendo la altura del orificio

Sea la fórmula:

$\displaystyle v=\sqrt{2gh}$

despejando a "h"

$\displaystyle {{v}^{2}}={{\left( \sqrt{2gh} \right)}^{2}}$

$\displaystyle {{v}^{2}}=2gh$

$\displaystyle \frac{{{v}^{2}}}{2g}=h$

Invirtiendo la igualdad

$\displaystyle h=\frac{{{v}^{2}}}{2g}$

Sustituyendo nuestros datos en la fórmula:

$\displaystyle h=\frac{{{v}^{2}}}{2g}=\frac{{{\left( 13.5\frac{m}{s} \right)}^{2}}}{2\left( 9.8\frac{m}{{{s}^{2}}} \right)}=\frac{182.25\frac{{{m}^{2}}}{{{s}^{2}}}}{19.6\frac{m}{{{s}^{2}}}}=9.3m$

Es decir, que la altura del orificio deberá ser de 9.3 metros aproximadamente, ya que hemos redondeado la cantidad.

Resultado:

$\displaystyle h=9.3m$

Deja una respuesta Cancelar la respuesta