Solución Problema 3 Presión

El último ejemplo corresponde a un ejercicio basado en el Principio de Pascal del tema de Presión. Nuevamente comentamos que este ejercicio ayudará a reforzar los conocimientos adquiridos en el área de la hidrostática. Recuerden que con este ejemplo resuelto paso a paso ayudará al alumno a poder corroborar su respuesta y verificar si ha llegado al mismo resultado. 😀

Nivel de Dificultad: ⭐⭐⭐

Solución:

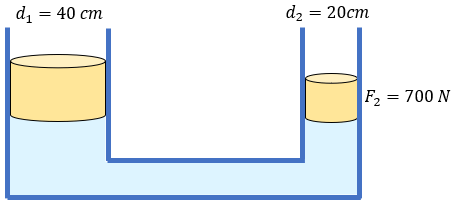
En el principio de Pascal, vemos que nos piden obtener la magnitud de la fuerza en el émbolo mayor. Y nos proporcionan dos diámetros que corresponden a los émbolos. Entonces.

• Obtener la magnitud de la fuerza en émbolo mayor

Datos:

$latex \displaystyle {{d}_{1}}=40cm=0.4m$

$latex \displaystyle {{d}_{2}}=20cm=0.2m$

$latex \displaystyle {{F}_{2}}=f=700N$

Observe que hemos convertido los centímetros a metros, para manejar las cantidades en el Sistema Internacional.

a) Magnitud de la fuerza del émbolo mayor

Basándonos en la fórmula:

$latex \displaystyle \frac{f}{a}=\frac{F}{A}$

Despejamos a "F" , tendremos lo siguiente:

$latex \displaystyle F=\frac{f\cdot A}{a}$

Pero lo primero es obtener el área de los émbolos.

$latex \displaystyle A=\frac{\pi {{d}_{1}}^{2}}{4}=\frac{\pi {{(0.4m)}^{2}}}{4}=0.1256{{m}^{2}}$

Luego el siguiente émbolo

$latex \displaystyle a=\frac{\pi {{d}_{2}}^{2}}{4}=\frac{\pi {{(0.2m)}^{2}}}{4}=0.0314{{m}^{2}}$

Sustituyendo en la fórmula para obtener la magnitud:

$latex \displaystyle F=\frac{f\cdot A}{a}=\frac{\left( 700N \right)\left( 0.1256{{m}^{2}} \right)}{0.0314{{m}^{2}}}=2800N$

Lo que nos proporciona una fuerza de 2800 Newtons

Respuesta:

$latex \displaystyle F=2800N$