Solución Problema 4 ley de Coulomb
Este ejercicio contiene información importante acerca del comportamiento de un electrón o protón al momento de someterce a fuerzas de atracción o repulsión.
Nivel de dificultad: ⭐⭐⭐
Problema 7. Dos protones están a cada lado de un electrón como se muestra en la imagen, considerando que el electrón está a 30 µm del protón a su izquierda y a 10 µm del protón a su derecha. ¿Cuál es la magnitud y la dirección de la fuerza eléctrica neta que actúa sobre el electrón?
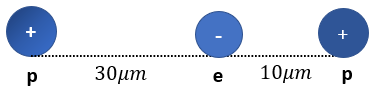
Considere lo siguiente:
$\displaystyle k=8.99\cdot {{10}^{9}}\frac{{N\cdot {{m}^{2}}}}{{{{C}^{2}}}}$
$\displaystyle p=+1.60\cdot {{10}^{{-19}}}C$
Solución:
La fuerza neta sobre el electrón es la suma de las fuerzas entre el electrón y cada uno de los protones:
$\displaystyle {{F}_{{neta}}}={{F}_{1}}+{{F}_{2}}$
Estas fuerzas vienen dadas por la ley de Coulomb:
$\displaystyle F=k\frac{{{{q}_{1}}{{q}_{2}}}}{{{{r}^{2}}}}$
Colocando nuestros datos, obtenemos las fuerzas individuales:
$\displaystyle F_1=(8.99\cdot10^9)\frac{(+1.60 \cdot 10^{-19})(-1.60 \cdot 10^{-19})}{(30 \cdot 10^-6)^2} = 2.56 \cdot 10^{-19} N$
$\displaystyle F_2=(8.99\cdot10^9)\frac{(+1.60 \cdot 10^{-19})(-1.60 \cdot 10^{-19})}{(10 \cdot 10^-6)^2} = 2.30 \cdot 10^{-18} N$
Debido a que las cargas opuestas se atraen, F1 apunta a la izquierda (la dirección negativa) y F2 apunta a la derecha (la dirección positiva). Por lo tanto, la fuerza neta es:
$\displaystyle F_{neta} = -2.56 \cdot 10^{-19} N + 2.30 \cdot 10^{-18} N = 2.04 \cdot 10^{-18}N$
Debido a que este valor es positivo, la dirección es hacia la derecha.
Deja una respuesta