Suma de Matrices - Ejercicios Resueltos

¡Hola, amigos de Fisimat! Si alguna vez te has preguntado cómo organizar grandes cantidades de datos o resolver sistemas de ecuaciones de forma eficiente, estás en el lugar correcto. Las matrices son herramientas increíblemente poderosas en el mundo de la ingeniería, la física, la computación y muchas otras disciplinas. Forman parte esencial del álgebra lineal y nos permiten ordenar información para abordar problemas complejos de una manera más estructurada y sencilla.

Sabemos que al principio, una matriz llena de números puede parecer intimidante. ¡Pero no te preocupes! En este post, nos vamos a enfocar en los fundamentos, trabajando principalmente con matrices cuadradas (aquellas que tienen el mismo número de filas que de columnas) como las de tamaño 2×2, 3×3 y, ocasionalmente, 4×4. Comenzaremos con ejemplos sencillos para que domines la base, y dejaremos los desafíos más complejos para el final.

Hoy, nuestro objetivo es claro: aprenderás cómo sumar matrices paso a paso. Verás que es una operación más intuitiva de lo que imaginas. ¡Empecemos! 🤓

¿Qué es una Matriz?

Antes de saltar a la suma, refresquemos rápidamente qué es una matriz. Imagina una tabla o una cuadrícula donde organizas números (o incluso expresiones) en filas y columnas. ¡Eso es una matriz! Esta organización es clave porque nos ayuda a:

• Representar sistemas de ecuaciones lineales.
• Manejar datos de manera ordenada (pensemos en hojas de cálculo).
• Realizar transformaciones geométricas (como rotaciones o escalados en gráficos por computadora).
• Y mucho más que descubrirás en tu viaje por el álgebra lineal.

Cada matriz tiene un "tamaño" o "dimensión", que se define por su número de filas y columnas. Por ejemplo, una matriz con 2 filas y 3 columnas es una matriz de dimensión 2×3.

Entendiendo los Componentes: Filas o Renglones, Columnas y Elementos

Como mencionaste, una matriz se compone de filas/renglones (horizontales) y columnas (verticales). Cada número dentro de la matriz se llama elemento o componente. Para identificar un elemento específico, usamos una notación de subíndices: $\displaystyle {{a}_{{ij}}}$, dónde $\displaystyle i$ representa el número de la fila y $\displaystyle j$
el número de la columna donde se encuentra el elemento.

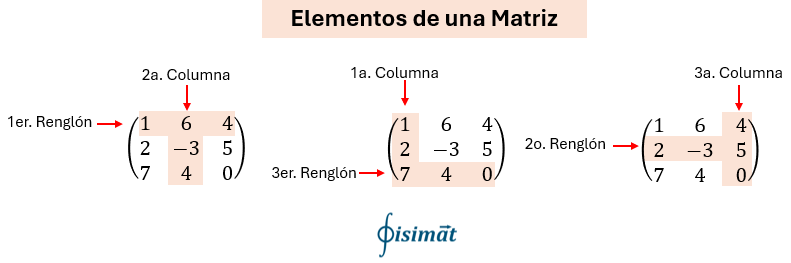
Comprender esto es fundamental, porque la suma de matrices depende directamente de la posición de estos elementos.

¿Cuándo podemos sumar Matrices?

Aquí viene la parte crucial y muy sencilla: solo puedes sumar dos matrices si tienen exactamente el mismo tamaño (las mismas dimensiones). Es decir, deben tener el mismo número de filas y el mismo número de columnas.

• ¿Puedes sumar una matriz 2×3 con otra 2×3? ¡Sí!
• ¿Puedes sumar una matriz 3×3 con otra 3×3? ¡Absolutamente!
• ¿Puedes sumar una matriz 2×2 con una 2×3? ¡No! Serían incompatibles para la suma.

Si intentas sumar matrices de diferentes tamaños, la operación simplemente no está definida. ¡Así de fácil es la regla principal!

¿Cómo podemos sumar Matrices? El Proceso Paso a Paso

Una vez que hemos verificado que nuestras matrices tienen el mismo tamaño, el proceso de suma es muy directo: la suma de dos matrices A y B, resulta en una nueva matriz C (del mismo tamaño que A y B), donde cada elemento de C es la suma de los elementos correspondientes de A y B.

Es decir, si $\displaystyle C=A+B$ , entonces cada elemento $\displaystyle {{c}_{{ij}}}$ de la matriz $\displaystyle C$ se calcula como $\displaystyle {{c}_{{ij}}}={{a}_{{ij}}}+{{b}_{{ij}}}$

Fórmula General de la Suma de Matrices

Si tenemos dos matrices A y B, de dimensión m × n , entonces el resultado de la matriz será como se muestra:

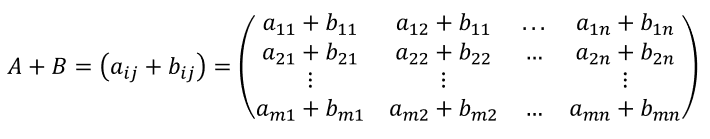
Observa con atención: el elemento en la primera fila y primera columna de la suma A + B, es la suma del elemento en la primera fila y primera columna de A y el elemento en la primera fila y primera columna de B. Y así sucesivamente con todos los demás elementos.

Propiedades Importantes de la Suma de Matrices

La suma de matrices cumple con ciertas propiedades que son útiles de conocer, especialmente si continuarás estudiando álgebra lineal:

Propiedad Conmutativa:

El orden en que sumas las matrices no altera el resultado.

$\displaystyle A+B=B+A$

Propiedad Asociativa:

Si sumas tres o más matrices, puedes agruparlas de diferentes maneras y el resultado será el mismo.

$\displaystyle \left( {A+B} \right)+C=A+\left( {B+C} \right)$

Elemento Neutro Aditivo (Matriz Cero):

Existe una matriz especial, llamada matriz cero (todos sus elementos son 0), que al sumarla a cualquier matriz A, da como resultado la misma matriz A

$\displaystyle A+0=A$

Elemento Inverso Aditivo (Matriz Opuesta):

Para cada matriz A, existe una matriz opuesta −A (cuyos elementos son los opuestos de los elementos de A) tal que su suma es la matriz cero.

$\displaystyle A+(-A)=0$

Estas propiedades son similares a las que ya conoces de la suma de números reales.

Ejemplos Resueltos de Suma de Matrices

Llego el momento de resolver ejercicios de suma de matrices. ¿Estás listo?

$\displaystyle A=\left( \begin{matrix}
-3 & 2 \\
1 & -2 \\
\end{matrix} \right)$

$\displaystyle B=\left( \begin{matrix}
4 & 1 \\
3 & 3 \\
\end{matrix} \right)$

Solución:

Para sumar las matrices $A$ y $B$, sumamos los elementos correspondientes:

$\displaystyle A+B = \left( \begin{matrix}
-3 & 2 \\
1 & -2 \\
\end{matrix} \right)+\left( \begin{matrix}
4 & 1 \\
3 & 3 \\
\end{matrix} \right)=\left( \begin{matrix}
-3+4 & 2+1 \\
1+3 & -2+3 \\
\end{matrix} \right)$

Realizando las operaciones en cada elemento:

$\displaystyle A+B=\left( \begin{matrix}
1 & 3 \\
4 & 1 \\
\end{matrix} \right)$

$\displaystyle C=\left( \begin{matrix}
5 & -8 \\
-2 & 0 \\
\end{matrix} \right)$

$\displaystyle D=\left( \begin{matrix}
-7 & 3 \\
-4 & 9 \\
\end{matrix} \right)$

Solución:

Sumamos los elementos que ocupan la misma posición en ambas matrices:

$\displaystyle C+D = \left( \begin{matrix}
5 & -8 \\
-2 & 0 \\
\end{matrix} \right)+\left( \begin{matrix}
-7 & 3 \\
-4 & 9 \\
\end{matrix} \right)=\left( \begin{matrix}
5+(-7) & -8+3 \\
-2+(-4) & 0+9 \\
\end{matrix} \right)$
El resultado es:
$\displaystyle C+D=\left( \begin{matrix}
-2 & -5 \\
-6 & 9 \\
\end{matrix} \right)$

$\displaystyle E=\left( \begin{matrix}
1 & 2 & 3 \\
4 & 5 & 6 \\
7 & 8 & 9 \\
\end{matrix} \right)$
$\displaystyle F=\left( \begin{matrix}
9 & -1 & 0 \\
-2 & 8 & -3 \\
5 & -4 & 7 \\
\end{matrix} \right)$

Solución:

Ambas matrices son de $3 \times 3$, así que procedemos a sumar los elementos correspondientes:

$\displaystyle E+F = \left( \begin{matrix}
1+9 & 2+(-1) & 3+0 \\
4+(-2) & 5+8 & 6+(-3) \\
7+5 & 8+(-4) & 9+7 \\
\end{matrix} \right)$

La matriz resultante es:

$\displaystyle E+F=\left( \begin{matrix}
10 & 1 & 3 \\
2 & 13 & 3 \\
12 & 4 & 16 \\
\end{matrix} \right)$

$\displaystyle G=\left( \begin{matrix}
10 & 20 & 30 \\
-5 & 15 & -25 \\
\end{matrix} \right)$
$\displaystyle H=\left( \begin{matrix}
-8 & 2 & -12 \\
6 & -10 & 18 \\
\end{matrix} \right)$

Solución:

Las matrices $G$ y $H$ son ambas de dimensión $2 \times 3$. Sumamos:

$\displaystyle G+H = \left( \begin{matrix}
10+(-8) & 20+2 & 30+(-12) \\
-5+6 & 15+(-10) & -25+18 \\
\end{matrix} \right)$

El resultado es:

$\displaystyle G+H=\left( \begin{matrix}
2 & 22 & 18 \\
1 & 5 & -7 \\
\end{matrix} \right)$

$\displaystyle J=\left( \begin{matrix}
\frac{1}{2} & -4 \\
0 & \sqrt{2} \\
\end{matrix} \right)$

$\displaystyle O=\left( \begin{matrix}
0 & 0 \\
0 & 0 \\
\end{matrix} \right)$

Solución:

La matriz cero $O$ tiene todos sus elementos iguales a cero.

$\displaystyle J+O = \left( \begin{matrix}
\frac{1}{2}+0 & -4+0 \\
0+0 & \sqrt{2}+0 \\
\end{matrix} \right)$

Como se esperaba, el resultado es la matriz original $J$:

$\displaystyle J+O=\left( \begin{matrix}
\frac{1}{2} & -4 \\
0 & \sqrt{2} \\
\end{matrix} \right)$

$\displaystyle K=\left( \begin{matrix}
7 & -1 \\
-5 & 3 \\
0 & -2 \\
\end{matrix} \right)$

Solución:

Primero, encontramos la matriz opuesta $-K$, que se obtiene cambiando el signo de cada elemento de $K$:

$\displaystyle -K=\left( \begin{matrix}
-7 & 1 \\
5 & -3 \\
0 & 2 \\
\end{matrix} \right)$

Ahora, sumamos $K$ y $-K$:

$\displaystyle K+(-K) = \left( \begin{matrix}
7+(-7) & -1+1 \\
-5+5 & 3+(-3) \\
0+0 & -2+2 \\
\end{matrix} \right)$

El resultado es la matriz cero de dimensión $3 \times 2$:

$\displaystyle K+(-K)=\left( \begin{matrix}
0 & 0 \\
0 & 0 \\
0 & 0 \\
\end{matrix} \right)$

$\displaystyle L=\left( \begin{matrix}
1 & 2 \\
3 & 4 \\
\end{matrix} \right)$

$\displaystyle M=\left( \begin{matrix}
5 & 6 & 7 \\
8 & 9 & 10 \\
\end{matrix} \right)$

Solución:

Observamos las dimensiones de las matrices:
La matriz $L$ es de dimensión $2 \times 2$.
La matriz $M$ es de dimensión $2 \times 3$.

Dado que las matrices no tienen las mismas dimensiones (difieren en el número de columnas), la suma $L+M$ no está definida. No es posible realizar esta operación.

$\displaystyle P=\left( \begin{matrix}
a & b \\
c & d \\
\end{matrix} \right)$

$\displaystyle Q=\left( \begin{matrix}
x & y \\
z & w \\
\end{matrix} \right)$

Solución:

Ambas matrices son de $2 \times 2$. Sumamos los elementos correspondientes término a término:

$\displaystyle P+Q = \left( \begin{matrix}
a+x & b+y \\
c+z & d+w \\
\end{matrix} \right)$

El resultado es una nueva matriz donde cada elemento es la suma de las expresiones algebraicas correspondientes. Este tipo de operación es fundamental en demostraciones y desarrollos teóricos del álgebra lineal.

Conclusión

Aunque parezca una operación simple, la suma de matrices tiene aplicaciones prácticas en el procesamiento de imágenes, ya que las matrices pueden presentarse como matrices de pixeles, también podemos usarla como para modelar ciertos valores a lo largo del tiempo en sistemas dinámicos, las matrices sumadas representan diferententes influencias o estados. En resumen:

• Definición de Matriz: Un arreglo rectangular de números en filas y columnas.
• Condición para Sumar: Las matrices DEBEN tener las mismas dimensiones (mismo número de filas y mismo número de columnas).
• Proceso de Suma: Se suman los elementos que ocupan la misma posición en cada matriz para obtener el elemento correspondiente en la matriz resultante.
• Propiedades: La suma de matrices es conmutativa, asociativa, tiene un elemento neutro (matriz cero) y un elemento inverso (matriz opuesta).