Esfuerzo y Deformación - Ejercicios Resueltos
¡Qué tal amigos de Fisimat!, iniciamos una serie de publicaciones dedicadas a explorar el fascinante tema de la elasticidad en los materiales. En esta primera entrega, sentaremos las bases al abordar los conceptos cruciales de esfuerzo y deformación unitaria, fundamentales para comprender cómo los cuerpos responden a las fuerzas. A lo largo de esta serie, también cubriremos temas como: la Ley de Hooke, el Módulo de Young, el Módulo de Corte, el Módulo Volumétrico, el Coeficiente de Poisson, el Límite Elástico y la Curva Esfuerzo-Deformación completa.
Introducción
Cuando una fuerza actúa sobre un objeto sólido, este tiende a cambiar su forma y/o tamaño. Internamente, el material del objeto resiste estos cambios mediante fuerzas que se oponen a la deformación. Los conceptos de esfuerzo y deformación unitaria son pilares en la física y la ingeniería, ya que nos permiten cuantificar tanto las fuerzas internas generadas dentro de los materiales como los cambios dimensionales que experimentan. Comprender el esfuerzo y la deformación es crucial para el diseño y análisis de cualquier estructura o componente mecánico, desde puentes y edificios hasta implantes biomédicos y componentes de naves espaciales.
Las aplicaciones prácticas de estos conceptos son omnipresentes. En ingeniería civil, se utilizan para asegurar que las estructuras puedan soportar las cargas esperadas sin fallar. En ingeniería mecánica, son esenciales para diseñar máquinas y motores cuyos componentes resistan las tensiones de operación. En ciencia de materiales, el estudio de la relación entre esfuerzo y deformación permite caracterizar las propiedades mecánicas de nuevos materiales. Incluso en biomecánica, estos conceptos ayudan a entender cómo los tejidos biológicos como huesos y tendones responden a las fuerzas.
¿Qué es el Esfuerzo?
El esfuerzo ($\sigma$ o $\tau$) es una medida de la intensidad de las fuerzas internas que las partículas de un cuerpo ejercen entre sí por unidad de área. Estas fuerzas internas son una reacción del material a las fuerzas externas aplicadas que tienden a deformarlo. Se calcula como la fuerza aplicada dividida por el área sobre la cual actúa dicha fuerza.
La fórmula general para el esfuerzo promedio es:
$$\sigma_{prom} = \frac{F}{A}$$
Donde:
$F$ es la magnitud de la fuerza interna resultante o la fuerza externa aplicada.
$A$ es el área sobre la cual actúa la fuerza.
Las unidades del esfuerzo en el Sistema Internacional (SI) son Newton por metro cuadrado ($N/m^2$), que se conocen como Pascales (Pa). Dado que el Pascal es una unidad pequeña, a menudo se utilizan múltiplos como el kilopascal (kPa), megapascal (MPa) o gigapascal (GPa).
(ingresar imagen: Diagrama de un cuerpo sometido a una fuerza externa F, mostrando el área A de sección transversal y las fuerzas internas distribuidas sobre esa área.)
Tipos de Esfuerzo
El esfuerzo se clasifica principalmente según la orientación de la fuerza con respecto al área sobre la que actúa.
Esfuerzo Normal ($\sigma$)
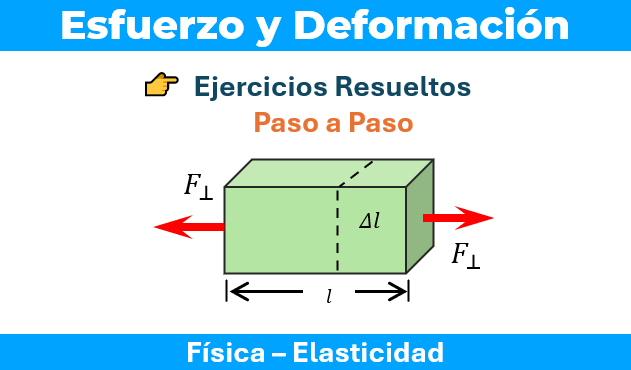
El esfuerzo normal se produce cuando la dirección de la fuerza aplicada es perpendicular (normal) al área considerada. Este tipo de esfuerzo tiende a causar un cambio en la longitud del cuerpo (alargamiento o acortamiento) o en su volumen. La fórmula es:
$$\sigma = \frac{F_{\perp}}{A}$$
Donde $F_{\perp}$ es la componente de la fuerza perpendicular al área $A$.
Existen dos tipos de esfuerzo normal:
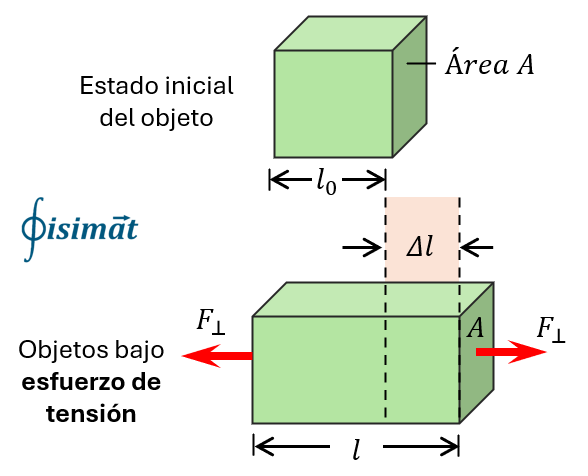
1. Esfuerzo de Tracción (o Tensión)
El esfuerzo de tracción ocurre cuando las fuerzas aplicadas tienden a estirar o alargar el cuerpo. Las fuerzas actúan hacia afuera del cuerpo, tirando del material. Un ejemplo común es una cuerda que sostiene un peso.
Ejemplo básico: Una barra de acero con un área de sección transversal de $0.0005 \text{ m}^2$ está sometida a una fuerza de tracción de $10,000 \text{ N}$. El esfuerzo de tracción es:
$\sigma = \frac{10000 \text{ N}}{0.0005 \text{ m}^2} = 20,000,000 \text{ Pa} = 20 \text{ MPa}$
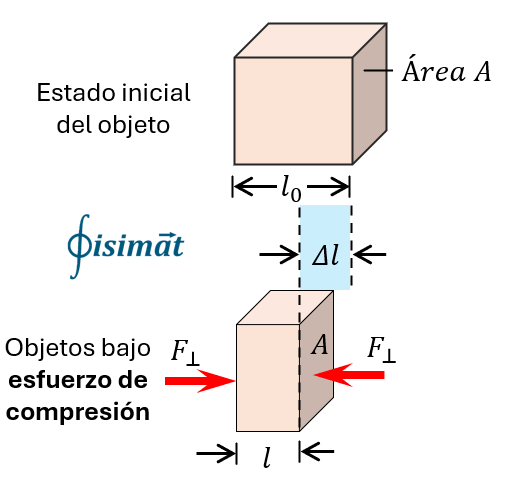
2. Esfuerzo de Compresión
El esfuerzo de compresión ocurre cuando las fuerzas aplicadas tienden a acortar o aplastar el cuerpo. Las fuerzas actúan hacia adentro del cuerpo, empujando el material. Un ejemplo es una columna que soporta el peso de un techo.
Ejemplo básico: Un pilar de concreto con un área de sección transversal de $0.04 \text{ m}^2$ soporta una carga de $80,000 \text{ N}$. El esfuerzo de compresión es:
$\sigma = \frac{80000 \text{ N}}{0.04 \text{ m}^2} = 2,000,000 \text{ Pa} = 2 \text{ MPa}$
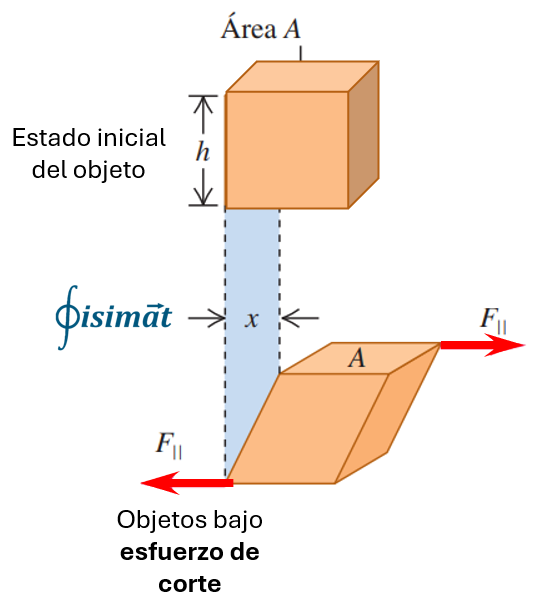
Esfuerzo Cortante o Tangencial ($\tau$)
El esfuerzo cortante (también llamado esfuerzo tangencial o de cizalladura) se produce cuando la dirección de la fuerza aplicada es paralela al área considerada. Este tipo de esfuerzo tiende a causar que una porción del cuerpo se deslice o corte con respecto a otra porción adyacente. La fórmula es:
$$\tau = \frac{F_{\parallel}}{A}$$
Donde $F_{\parallel}$ es la componente de la fuerza paralela al área $A$.
Ejemplo básico: Dos placas están unidas por un remache de $1 \text{ cm}$ de radio (Área de sección del remache $\approx \pi (0.01 \text{ m})^2 \approx 3.1416 \times 10^{-4} \text{ m}^2$). Si se aplica una fuerza de $3000 \text{ N}$ que tiende a deslizar una placa sobre la otra, el esfuerzo cortante en el remache es:
$\tau = \frac{3000 \text{ N}}{3.1416 \times 10^{-4} \text{ m}^2} \approx 9,549,296 \text{ Pa} \approx 9.55 \text{ MPa}$
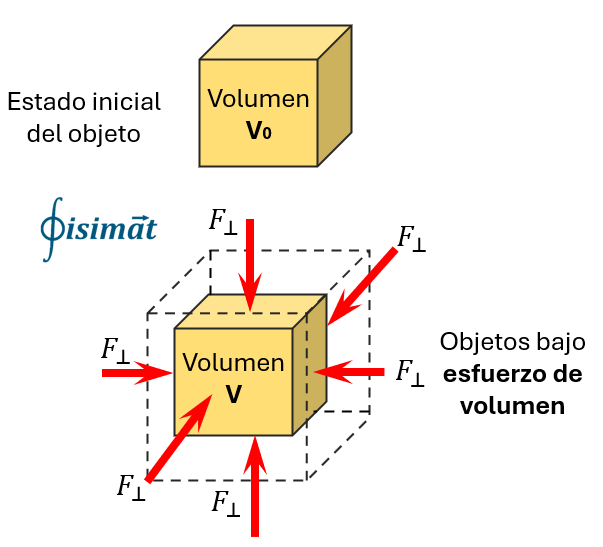
Esfuerzo Volumétrico (Presión)
Aunque a menudo se trata como un tipo de esfuerzo normal (cuando es uniforme en todas las direcciones), el esfuerzo volumétrico o presión hidrostática ($P$) merece una mención. Ocurre cuando un cuerpo está sometido a fuerzas externas que actúan perpendicularmente sobre toda su superficie, como un objeto sumergido en un fluido. Este esfuerzo tiende a cambiar el volumen total del cuerpo sin cambiar su forma (si el material es isótropo).
$$P = \frac{F}{A}$$
Aquí, $F$ es la fuerza normal que actúa sobre una porción de área $A$ de la superficie del cuerpo.
¿Qué es la Deformación Unitaria?
La deformación unitaria (a menudo simplemente llamada deformación) es una medida de la intensidad de la deformación experimentada por un cuerpo como resultado de la aplicación de un esfuerzo. Se define como el cambio relativo en una dimensión (longitud, ángulo o volumen) con respecto a su valor original. Es una cantidad adimensional, aunque a veces se expresa en porcentajes (%) o en unidades como micrómetros por metro ($\mu m/m$) o "microstrains" ($\mu\epsilon$).
Tipos de Deformación Unitaria
Correspondiendo a los tipos de esfuerzo, existen diferentes tipos de deformación unitaria.
Deformación Unitaria Longitudinal o Normal ($\epsilon$)
La deformación unitaria longitudinal (o normal) es el cambio en la longitud por unidad de la longitud original de un cuerpo, como resultado de un esfuerzo normal (de tracción o compresión). Se calcula como:
$$\epsilon = \frac{\Delta L}{L_0} = \frac{L_f - L_0}{L_0}$$
Donde:
$\epsilon$ (épsilon) es la deformación unitaria longitudinal.
$\Delta L$ es el cambio en la longitud ($L_f - L_0$).
$L_0$ es la longitud original.
$L_f$ es la longitud final.
Si $\epsilon > 0$, hay un alargamiento (deformación por tracción). Si $\epsilon < 0$, hay un acortamiento (deformación por compresión).
Ejemplo básico: Una varilla metálica de $2 \text{ m}$ de longitud original se estira hasta alcanzar una longitud final de $2.005 \text{ m}$ bajo un esfuerzo de tracción. La deformación unitaria longitudinal es:
$\Delta L = 2.005 \text{ m} - 2 \text{ m} = 0.005 \text{ m}$
$\epsilon = \frac{0.005 \text{ m}}{2 \text{ m}} = 0.0025$
Deformación Unitaria por Cizalladura o Cortante ($\gamma$)
La deformación unitaria por cizalladura (o cortante) es una medida de la distorsión angular de un cuerpo debido a un esfuerzo cortante. Se define como el cambio en el ángulo entre dos líneas que originalmente eran perpendiculares en el material. Para ángulos pequeños, se puede aproximar como el desplazamiento tangencial ($x$) de una cara del elemento dividida por la distancia perpendicular ($h$) a esa cara (altura).
$$\gamma = \tan \theta \approx \theta \text{ (para ángulos } \theta \text{ pequeños, expresados en radianes)}$$O también:$$\gamma = \frac{x}{h}$$
Donde:
$\gamma$ (gamma) es la deformación unitaria por cizalladura (en radianes).
$\theta$ es el cambio angular.
$x$ es el desplazamiento tangencial.
$h$ es la altura o distancia perpendicular.
Ejemplo básico: Un bloque de caucho de $10 \text{ cm}$ de altura experimenta un desplazamiento de su cara superior de $0.2 \text{ cm}$ debido a una fuerza cortante. La deformación unitaria por cizalladura es:
$\gamma = \frac{0.2 \text{ cm}}{10 \text{ cm}} = 0.02 \text{ rad}$
Deformación Unitaria Volumétrica ($\epsilon_V$)
La deformación unitaria volumétrica es el cambio en el volumen por unidad del volumen original de un cuerpo, como resultado de un esfuerzo volumétrico o presión hidrostática.
$$\epsilon_V = \frac{\Delta V}{V_0} = \frac{V_f - V_0}{V_0}$$
Donde:
$\epsilon_V$ es la deformación unitaria volumétrica.
$\Delta V$ es el cambio en el volumen ($V_f - V_0$).
$V_0$ es el volumen original.
$V_f$ es el volumen final.
Ejemplo básico: Un bloque de material con un volumen original de $0.1 \text{ m}^3$ se somete a una alta presión, reduciendo su volumen a $0.0998 \text{ m}^3$. La deformación unitaria volumétrica es:
$\Delta V = 0.0998 \text{ m}^3 - 0.1 \text{ m}^3 = -0.0002 \text{ m}^3$
$\epsilon_V = \frac{-0.0002 \text{ m}^3}{0.1 \text{ m}^3} = -0.002$
El signo negativo indica una reducción de volumen.
Relación entre Esfuerzo y Deformación
Es importante destacar que el esfuerzo aplicado a un material es lo que causa la deformación unitaria en él. La naturaleza de esta relación (cómo un material específico responde a un esfuerzo determinado con una cierta cantidad de deformación) es una propiedad intrínseca y fundamental de dicho material. Para muchos materiales, dentro de ciertos límites (la región elástica), el esfuerzo es directamente proporcional a la deformación, una relación descrita por la Ley de Hooke. Esta proporcionalidad se cuantifica mediante los llamados módulos elásticos (Módulo de Young, Módulo de Corte, Módulo Volumétrico), que indican la rigidez del material y serán el foco de nuestros próximos artículos.
Ejercicios Resueltos de Esfuerzo y Deformación
Aquí se presentarán entre 8 y 12 problemas de dificultad progresiva (Básico, Intermedio), cubriendo los conceptos de esfuerzo y deformación normal y cortante.
Problema 1. Una barra cilíndrica de aluminio tiene un diámetro de $2 \text{ cm}$ y una longitud de $50 \text{ cm}$. Si se le aplica una fuerza de tracción axial de $15 \text{ kN}$, ¿cuál es el esfuerzo normal en la barra?
Solución
▷ Paso 1 Calcular el radio de la barra.
El diámetro $d = 2 \text{ cm}$, por lo tanto, el radio $r = \frac{d}{2} = \frac{2 \text{ cm}}{2} = 1 \text{ cm} = 0.01 \text{ m}$.
▷ Paso 2 Calcular el área de la sección transversal ($A$) de la barra.
El área de un círculo es $A = \pi r^2$.
$A = \pi (0.01 \text{ m})^2 = \pi (0.0001 \text{ m}^2) \approx 3.14159 \times 10^{-4} \text{ m}^2$.
▷ Paso 3 Aplicar la fórmula del esfuerzo normal ($\sigma$).
La fuerza de tracción $F = 15 \text{ kN} = 15000 \text{ N}$.
$\sigma = \frac{F}{A}$
$\sigma = \frac{15000 \text{ N}}{3.14159 \times 10^{-4} \text{ m}^2} \approx 47746482.9 \text{ Pa}$
▷ Paso 4 Expresar el resultado en Megapascales (MPa).
$1 \text{ MPa} = 10^6 \text{ Pa}$.
$\sigma \approx \frac{47746482.9}{10^6} \text{ MPa} \approx 47.75 \text{ MPa}$.
Respuesta: El esfuerzo normal en la barra es aproximadamente $47.75 \text{ MPa}$.
Problema 2. Un cable de acero de $2 \text{ m}$ de longitud original se alarga $1.5 \text{ mm}$ cuando se somete a una carga. Calcula la deformación unitaria longitudinal.
Solución
▷ Paso 1 Identificar los datos proporcionados.
Longitud original $L_0 = 2 \text{ m}$.
Alargamiento $\Delta L = 1.5 \text{ mm}$.
▷ Paso 2 Convertir todas las unidades de longitud a la misma unidad (metros).
$\Delta L = 1.5 \text{ mm} = 1.5 \times 10^{-3} \text{ m} = 0.0015 \text{ m}$.
▷ Paso 3 Aplicar la fórmula de la deformación unitaria longitudinal ($\epsilon$).
$\epsilon = \frac{\Delta L}{L_0}$
$\epsilon = \frac{0.0015 \text{ m}}{2 \text{ m}} = 0.00075$.
Respuesta: La deformación unitaria longitudinal es $0.00075$ (o $750 \mu\epsilon$).
Problema 3. Una columna cuadrada de madera de $10 \text{ cm} \times 10 \text{ cm}$ de sección transversal soporta una carga de compresión de $50 \text{ kN}$. Determina el esfuerzo de compresión en la columna.
Solución
▷ Paso 1 Calcular el área de la sección transversal ($A$) de la columna.
Lado $s = 10 \text{ cm} = 0.1 \text{ m}$.
$A = s^2 = (0.1 \text{ m})^2 = 0.01 \text{ m}^2$.
▷ Paso 2 Identificar la fuerza de compresión.
$F = 50 \text{ kN} = 50000 \text{ N}$.
▷ Paso 3 Aplicar la fórmula del esfuerzo normal ($\sigma$).
$\sigma = \frac{F}{A}$
$\sigma = \frac{50000 \text{ N}}{0.01 \text{ m}^2} = 5,000,000 \text{ Pa}$.
▷ Paso 4 Expresar el resultado en Megapascales (MPa).
$\sigma = \frac{5,000,000}{10^6} \text{ MPa} = 5 \text{ MPa}$.
Respuesta: El esfuerzo de compresión en la columna es de $5 \text{ MPa}$.
Problema 4. Un bloque rectangular de un material de $8 \text{ cm}$ de altura sufre una deformación por cizalladura. La cara superior del bloque se desplaza $0.16 \text{ mm}$ horizontalmente con respecto a la base. Calcula la deformación unitaria por cizalladura ($\gamma$).
Solución
▷ Paso 1 Identificar los datos proporcionados.
Altura del bloque $h = 8 \text{ cm}$.
Desplazamiento tangencial $x = 0.16 \text{ mm}$.
▷ Paso 2 Convertir todas las unidades de longitud a la misma unidad (por ejemplo, milímetros).
$h = 8 \text{ cm} = 80 \text{ mm}$.
▷ Paso 3 Aplicar la fórmula de la deformación unitaria por cizalladura ($\gamma$).
$\gamma = \frac{x}{h}$
$\gamma = \frac{0.16 \text{ mm}}{80 \text{ mm}} = 0.002$.
Respuesta: La deformación unitaria por cizalladura es $0.002 \text{ rad}$.
Problema 5. Un cubo de metal de $10 \text{ cm}$ de arista ($V_0 = 1000 \text{ cm}^3$) es sometido a una presión hidrostática que reduce su volumen en $0.05 \text{ cm}^3$. Calcula la deformación unitaria volumétrica.
Solución
▷ Paso 1 Identificar los datos proporcionados.
Volumen original $V_0 = 1000 \text{ cm}^3$.
Cambio en el volumen $\Delta V = -0.05 \text{ cm}^3$ (negativo porque es una reducción).
▷ Paso 2 Aplicar la fórmula de la deformación unitaria volumétrica ($\epsilon_V$).
$\epsilon_V = \frac{\Delta V}{V_0}$
$\epsilon_V = \frac{-0.05 \text{ cm}^3}{1000 \text{ cm}^3} = -0.00005$.
Respuesta: La deformación unitaria volumétrica es $-0.00005$.
Problema 6. Un tornillo de $8 \text{ mm}$ de diámetro está sometido a una fuerza de cizalladura doble de $12 \text{ kN}$ (es decir, el tornillo se corta en dos secciones). ¿Cuál es el esfuerzo cortante promedio en cada sección de corte del tornillo?
Solución
▷ Paso 1 Calcular el radio del tornillo.
Diámetro $d = 8 \text{ mm}$, radio $r = 4 \text{ mm} = 0.004 \text{ m}$.
▷ Paso 2 Calcular el área de una sección transversal ($A$) del tornillo.
$A = \pi r^2 = \pi (0.004 \text{ m})^2 = \pi (1.6 \times 10^{-5} \text{ m}^2) \approx 5.0265 \times 10^{-5} \text{ m}^2$.
▷ Paso 3 Determinar la fuerza cortante que actúa sobre cada sección de corte.
La fuerza total es $F_{total} = 12 \text{ kN} = 12000 \text{ N}$.
Como es cizalladura doble, esta fuerza se distribuye en dos áreas de corte. La fuerza que soporta cada sección de corte es $F_{\parallel} = \frac{F_{total}}{2} = \frac{12000 \text{ N}}{2} = 6000 \text{ N}$.
(ingresar imagen: Diagrama de un tornillo en cizalladura doble, mostrando las dos secciones de corte.)
▷ Paso 4 Aplicar la fórmula del esfuerzo cortante ($\tau$) para una sección.
$\tau = \frac{F_{\parallel}}{A}$
$\tau = \frac{6000 \text{ N}}{5.0265 \times 10^{-5} \text{ m}^2} \approx 119366207 \text{ Pa}$.
▷ Paso 5 Expresar el resultado en Megapascales (MPa).
$\tau \approx \frac{119366207}{10^6} \text{ MPa} \approx 119.37 \text{ MPa}$.
Respuesta: El esfuerzo cortante promedio en cada sección de corte del tornillo es aproximadamente $119.37 \text{ MPa}$.
Problema 7. Una barra de $1.5 \text{ m}$ de longitud experimenta un esfuerzo de tracción que produce una deformación unitaria de $0.0012$. ¿Cuál es el alargamiento total ($\Delta L$) de la barra?
Solución
▷ Paso 1 Identificar los datos proporcionados.
Longitud original $L_0 = 1.5 \text{ m}$.
Deformación unitaria longitudinal $\epsilon = 0.0012$.
▷ Paso 2 Reorganizar la fórmula de la deformación unitaria longitudinal para despejar $\Delta L$.
Sabemos que $\epsilon = \frac{\Delta L}{L_0}$.
Por lo tanto, $\Delta L = \epsilon \times L_0$.
▷ Paso 3 Calcular el alargamiento total.
$\Delta L = 0.0012 \times 1.5 \text{ m} = 0.0018 \text{ m}$.
▷ Paso 4 (Opcional) Expresar el resultado en milímetros.
$\Delta L = 0.0018 \text{ m} = 1.8 \text{ mm}$.
Respuesta: El alargamiento total de la barra es $0.0018 \text{ m}$ o $1.8 \text{ mm}$.
Problema 8. (Nivel Intermedio) Un tubo de acero ($E_{acero} = 200 \text{ GPa}$) con un diámetro exterior de $50 \text{ mm}$ y un diámetro interior de $40 \text{ mm}$ se somete a una carga de tracción axial de $100 \text{ kN}$. Si su longitud es de $2 \text{ m}$, determina: a) El esfuerzo normal en el tubo. b) El alargamiento del tubo.
*(Nota: Para la parte b, se necesitaría el Módulo de Young, que se verá en un próximo artículo. Para este problema, nos centraremos solo en la parte a, o podríamos indicar que la parte b es un adelanto).*
Solución
*(Centrándonos en la parte a y omitiendo la b por ahora, ya que el Módulo de Young no se ha introducido en este artículo)*
▷ Paso 1 Calcular los radios exterior ($R$) e interior ($r$).
Diámetro exterior $D_e = 50 \text{ mm} \Rightarrow R = 25 \text{ mm} = 0.025 \text{ m}$.
Diámetro interior $D_i = 40 \text{ mm} \Rightarrow r = 20 \text{ mm} = 0.020 \text{ m}$.
▷ Paso 2 Calcular el área de la sección transversal del tubo ($A_{tubo}$).
El área de la sección transversal de un tubo es el área del círculo exterior menos el área del círculo interior.
$A_{tubo} = A_e - A_i = \pi R^2 - \pi r^2 = \pi (R^2 - r^2)$.
$A_{tubo} = \pi ((0.025 \text{ m})^2 - (0.020 \text{ m})^2)$
$A_{tubo} = \pi (0.000625 \text{ m}^2 - 0.000400 \text{ m}^2)$
$A_{tubo} = \pi (0.000225 \text{ m}^2) \approx 7.06858 \times 10^{-4} \text{ m}^2$.
(ingresar imagen: Sección transversal de un tubo mostrando el diámetro exterior e interior.)
▷ Paso 3 Identificar la fuerza de tracción.
$F = 100 \text{ kN} = 100000 \text{ N}$.
▷ Paso 4 Aplicar la fórmula del esfuerzo normal ($\sigma$).
$\sigma = \frac{F}{A_{tubo}}$
$\sigma = \frac{100000 \text{ N}}{7.06858 \times 10^{-4} \text{ m}^2} \approx 141471069 \text{ Pa}$.
▷ Paso 5 Expresar el resultado en Megapascales (MPa).
$\sigma \approx \frac{141471069}{10^6} \text{ MPa} \approx 141.47 \text{ MPa}$.
Respuesta (Parte a): El esfuerzo normal en el tubo es aproximadamente $141.47 \text{ MPa}$.
Conclusión
Los conceptos de esfuerzo y deformación unitaria son absolutamente esenciales para entender cómo los materiales se comportan bajo la acción de fuerzas. Hemos visto que el esfuerzo es una medida de las fuerzas internas por unidad de área, clasificándose principalmente en normal (tracción y compresión) y cortante. Por otro lado, la deformación unitaria cuantifica el cambio dimensional relativo del material, con tipos correspondientes como la deformación longitudinal, por cizalladura y volumétrica.
Estos conceptos no solo son teóricos, sino que forman la base para el análisis y diseño en innumerables campos de la ingeniería y la ciencia. La comprensión de cómo un esfuerzo induce una deformación es el primer paso para predecir la resistencia, la rigidez y la estabilidad de cualquier objeto o estructura. En los próximos artículos de esta serie sobre Elasticidad, profundizaremos en la relación lineal entre esfuerzo y deformación (Ley de Hooke) y exploraremos los módulos elásticos que caracterizan esta importante propiedad de los materiales.
¿Te gustó este contenido?
Únete a nuestra comunidad en WhatsApp o Telegram para recibir nuevos proyectos, tutoriales y noticias exclusivas.
Deja una respuesta
Estos temas te pueden interesar