Ley de Hooke - Ejercicios Resueltos

Continuamos con nuestra serie de artículos dedicados a la elasticidad. Después de haber explorado los conceptos fundamentales de esfuerzo y deformación unitaria, en esta entrega nos adentraremos en una de las leyes más importantes que describen el comportamiento elástico de los materiales: la Ley de Hooke. Esta ley es crucial para entender cómo los objetos, desde simples resortes hasta complejas estructuras, responden a las fuerzas aplicadas dentro de su rango elástico.

Introducción a la Ley de Hooke

La Ley de Hooke, nombrada así en honor al científico inglés del siglo XVII Robert Hooke, es un principio fundamental en la física y la ciencia de materiales que describe la relación entre la fuerza aplicada a un cuerpo elástico y la deformación resultante. Originalmente formulada para resortes, esta ley establece que, para deformaciones relativamente pequeñas, la fuerza necesaria para extender o comprimir un resorte es directamente proporcional a la distancia de esa extensión o compresión. Esta relación lineal es la base del comportamiento elástico predecible de muchos materiales. ¡Ojo! 👆

La importancia de la Ley de Hooke radica en su simplicidad y su amplia aplicabilidad. No solo es fundamental para el diseño y análisis de resortes utilizados en una infinidad de dispositivos mecánicos (como básculas, suspensiones de vehículos, relojes y juguetes), sino que también proporciona una aproximación útil para el comportamiento elástico de materiales sólidos bajo tracción, compresión o cizalladura, dentro de ciertos límites. Entender esta ley nos permite predecir cómo se deformarán las estructuras y cuánto se estirarán o comprimirán los materiales bajo carga, lo cual es esencial en ingeniería para garantizar la seguridad y funcionalidad de los diseños.

La Ley de Hooke para Resortes

La manifestación más clásica y didáctica de la Ley de Hooke se observa en el comportamiento de los resortes helicoidales.

Resortes Ideales y Fuerza Restauradora

Un resorte ideal es aquel que obedece perfectamente la Ley de Hooke, no tiene masa y no sufre deformaciones permanentes. Cuando un resorte ideal se estira o se comprime, ejerce una fuerza restauradora que se opone al desplazamiento y tiende a devolverlo a su posición de equilibrio (longitud natural).

La formulación matemática de la Ley de Hooke para la fuerza restauradora ($F_s$) ejercida por un resorte es:

$$F_s = -kx$$

Donde:

• $F_s$ es la fuerza restauradora ejercida por el resorte (en Newtons, N).
• $k$ es la constante del resorte o constante de rigidez (en N/m).
• $x$ es el desplazamiento del extremo del resorte desde su posición de equilibrio (en metros, m). Si $x > 0$, el resorte está estirado; si $x < 0$, el resorte está comprimido.

Si consideramos la fuerza externa ($F_{aplicada}$) necesaria para producir el desplazamiento $x$, esta fuerza es igual en magnitud y opuesta en dirección a la fuerza restauradora (asumiendo que el proceso es lento y sin aceleración):

$$F_{aplicada} = kx$$

Solución:

a) ¿Qué fuerza restauradora ejerce el resorte si se estira $0.05 \text{ m}$ desde su posición de equilibrio?

$F_s = -kx = -(200 \text{ N/m})(0.05 \text{ m}) = -10 \text{ N}$.

(La fuerza es de $10 \text{ N}$ en dirección opuesta al estiramiento).

b) ¿Qué fuerza se debe aplicar para mantenerlo estirado $0.05 \text{ m}$?

$F_{aplicada} = kx = (200 \text{ N/m})(0.05 \text{ m}) = 10 \text{ N}$.

(En la dirección del estiramiento).

Constante del Resorte (k)

La constante del resorte ($k$), también conocida como constante de rigidez o coeficiente de elasticidad del resorte, es una medida de la "dureza" o rigidez del resorte. Indica cuánta fuerza se necesita para estirar o comprimir el resorte una unidad de longitud.

• Sus unidades en el Sistema Internacional son Newton por metro (N/m).
• Un valor alto de $k$ significa que el resorte es muy rígido (difícil de estirar o comprimir).
• Un valor bajo de $k$ significa que el resorte es blando o flexible (fácil de estirar o comprimir).

La constante $k$ depende de las propiedades del material del resorte (como su Módulo de Young), de su geometría (diámetro del alambre, diámetro del resorte, número de espiras) y de cómo está fabricado.

Solución:

Para el resorte A: $k_A = \frac{F}{x_A} = \frac{20 \text{ N}}{0.1 \text{ m}} = 200 \text{ N/m}$.

Para el resorte B: $k_B = \frac{F}{x_B} = \frac{20 \text{ N}}{0.05 \text{ m}} = 400 \text{ N/m}$.

El resorte B ($k_B = 400 \text{ N/m}$) es más rígido que el resorte A ($k_A = 200 \text{ N/m}$), ya que se necesita más fuerza para producir el mismo estiramiento, o bien, la misma fuerza produce un menor estiramiento.

Representación Gráfica: Fuerza vs. Desplazamiento

Si se grafica la fuerza aplicada ($F_{aplicada}$) a un resorte ideal en función de su desplazamiento ($x$) desde la posición de equilibrio, se obtiene una línea recta que pasa por el origen. La pendiente de esta recta es igual a la constante del resorte, $k$.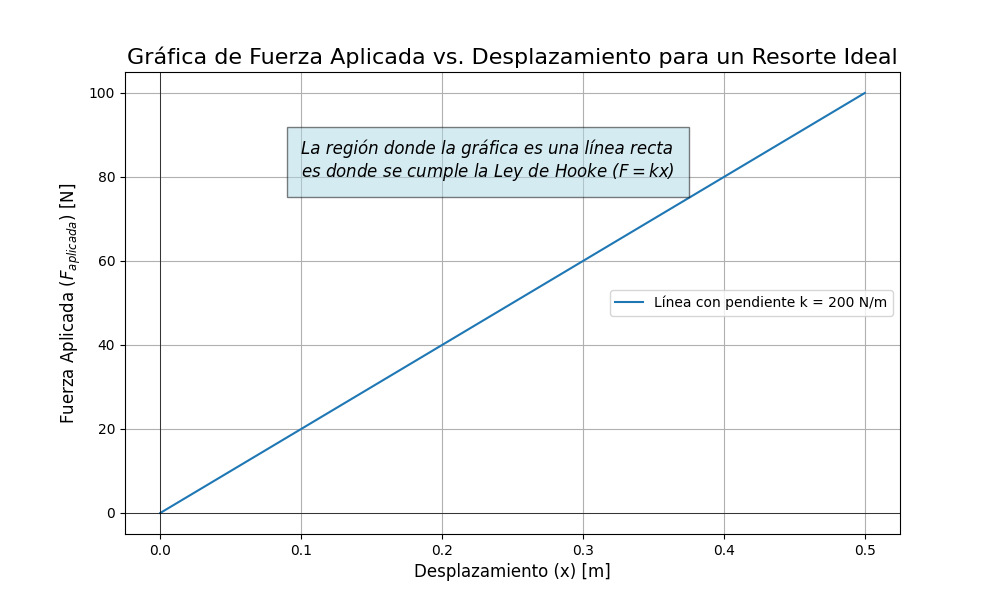

Generalización de la Ley de Hooke para Materiales Sólidos

La Ley de Hooke no se limita solo a resortes. Puede generalizarse para describir el comportamiento elástico de materiales sólidos sometidos a esfuerzos de tracción, compresión o cizalladura, siempre que las deformaciones sean pequeñas y no se exceda el límite elástico del material.

Esfuerzo y Deformación en la Región Elástica

Como vimos en el artículo anterior, el esfuerzo ($\sigma$) es la fuerza por unidad de área, y la deformación unitaria ($\epsilon$) es el cambio relativo en la dimensión. Para muchos materiales, dentro de un rango conocido como la región elástica, el esfuerzo es directamente proporcional a la deformación unitaria. Esta es la forma generalizada de la Ley de Hooke.

Módulo de Elasticidad (Módulo de Young)

Para un esfuerzo normal (tracción o compresión), la Ley de Hooke generalizada se expresa como:

$$\sigma = E\epsilon$$

Donde:

• $\sigma$ es el esfuerzo normal.
• $\epsilon$ es la deformación unitaria longitudinal.
• $E$ es la constante de proporcionalidad, conocida como el Módulo de Elasticidad o Módulo de Young.

El Módulo de Young ($E$) es una medida de la rigidez intrínseca de un material sólido. Cuanto mayor es el valor de $E$, más rígido es el material (es decir, se necesita un mayor esfuerzo para producir una determinada deformación unitaria). Sus unidades son las mismas que las del esfuerzo (Pascales, Pa). Este módulo es análogo a la constante $k$ de un resorte, pero es una propiedad del material en sí, independiente de su forma o tamaño.

(Este tema del Módulo de Young y otros módulos se explorará con mayor detalle en el próximo artículo de la serie de elasticidad).

Solución:

$\sigma = E\epsilon = (70 \times 10^9 \text{ Pa})(0.001) = 70 \times 10^6 \text{ Pa} = 70 \text{ MPa}$.

Límite de Proporcionalidad y Límite Elástico

Es crucial recordar que la Ley de Hooke (tanto en su forma para resortes como para materiales) solo es válida hasta un cierto punto llamado límite de proporcionalidad, donde la relación entre fuerza/desplazamiento o esfuerzo/deformación deja de ser lineal. Muy cerca de este punto se encuentra el límite elástico; si el material se deforma más allá de este límite, sufrirá una deformación permanente (no volverá a su forma original al retirar la carga). Estos límites son características importantes de cada material y se discutirán en detalle en un artículo posterior dedicado a la curva esfuerzo-deformación.

Energía Potencial Elástica

Cuando se deforma un cuerpo elástico (como al estirar un resorte o una barra), se realiza trabajo sobre él. Si la deformación ocurre dentro del límite elástico, este trabajo se almacena en el cuerpo como energía potencial elástica ($U_e$).

Energía Almacenada en un Resorte Deformado

El trabajo realizado ($W$) para estirar o comprimir un resorte una distancia $x$ desde su posición de equilibrio es igual al área bajo la gráfica de $F_{aplicada}$ vs. $x$. Dado que $F_{aplicada} = kx$, la gráfica es una línea recta, y el área es un triángulo.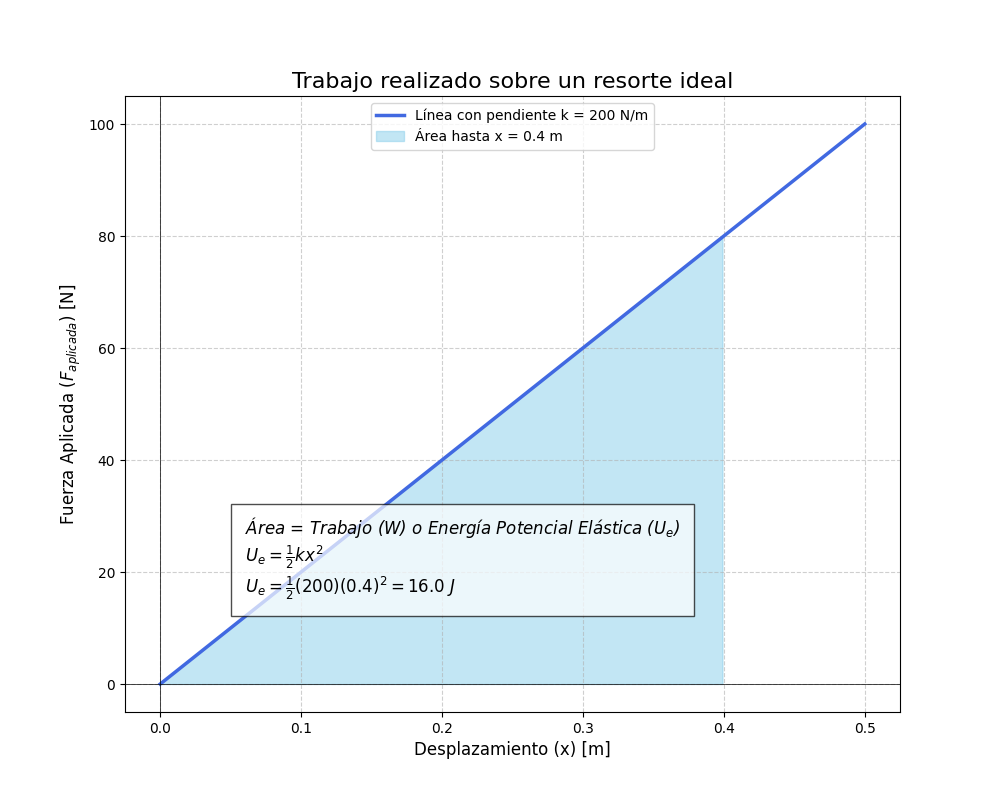La energía potencial elástica almacenada en un resorte deformado una distancia $x$ es:

$$U_e = \frac{1}{2}kx^2$$

Otras formas equivalentes, usando $F_{aplicada} = kx$, son:

$$U_e = \frac{1}{2}F_{aplicada}x$$
$$U_e = \frac{F_{aplicada}^2}{2k}$$

Las unidades de la energía potencial elástica son Joules (J) en el SI.

Solución:

$U_e = \frac{1}{2}kx^2 = \frac{1}{2}(400 \text{ N/m})(0.05 \text{ m})^2 = \frac{1}{2}(400 \text{ N/m})(0.0025 \text{ m}^2) = 0.5 \text{ J}$.

Energía de Deformación en Materiales

De manera análoga, cuando un material sólido se deforma elásticamente debido a un esfuerzo, almacena energía de deformación. La energía de deformación por unidad de volumen (densidad de energía de deformación, $u_e$) para un material sometido a esfuerzo normal en la región elástica es:

$$u_e = \frac{1}{2}\sigma\epsilon$$

Usando $\sigma = E\epsilon$, podemos reescribir esto como:

$$u_e = \frac{1}{2}E\epsilon^2 = \frac{\sigma^2}{2E}$$

Esta energía se recupera si se permite que el material vuelva a su forma original.

Ejercicios Resueltos de la Ley de Hooke

Solución

▷ Paso 1 (a) Identificar los datos para calcular $k$.

Fuerza aplicada $F_{aplicada1} = 10 \text{ N}$.

Desplazamiento $x_1 = 5 \text{ cm} = 0.05 \text{ m}$.

▷ Paso 2 (a) Aplicar la Ley de Hooke para la fuerza aplicada ($F_{aplicada} = kx$) y despejar $k$.

$k = \frac{F_{aplicada1}}{x_1}$

$k = \frac{10 \text{ N}}{0.05 \text{ m}} = 200 \text{ N/m}$.

▷ Paso 3 (b) Usar la constante $k$ calculada y la nueva fuerza para hallar el nuevo alargamiento $x_2$.

Nueva fuerza aplicada $F_{aplicada2} = 25 \text{ N}$.

$F_{aplicada2} = kx_2 \Rightarrow x_2 = \frac{F_{aplicada2}}{k}$

$x_2 = \frac{25 \text{ N}}{200 \text{ N/m}} = 0.125 \text{ m}$.

▷ Paso 4 (b) Convertir el resultado a centímetros si se desea.

$x_2 = 0.125 \text{ m} = 12.5 \text{ cm}$.

Respuesta:
a) La constante del resorte es $200 \text{ N/m}$.
b) Un peso de $25 \text{ N}$ producirá un alargamiento de $0.125 \text{ m}$ o $12.5 \text{ cm}$.

Solución

▷ Paso 1 Identificar los datos proporcionados.

Constante del resorte $k = 500 \text{ N/m}$.

Desplazamiento $x = -8 \text{ cm}$ (negativo porque es una compresión).

▷ Paso 2 Convertir el desplazamiento a metros.

$x = -8 \text{ cm} = -0.08 \text{ m}$.

▷ Paso 3 Aplicar la fórmula de la fuerza restauradora ($F_s = -kx$).

$F_s = -(500 \text{ N/m})(-0.08 \text{ m})$

$F_s = +40 \text{ N}$.

Respuesta: La fuerza restauradora ejercida por el resorte es de $40 \text{ N}$ (en la dirección opuesta a la compresión, es decir, tratando de expandirse).

Solución

▷ Paso 1 Identificar los datos.

Constante del resorte $k = 300 \text{ N/m}$.
Desplazamiento $x = 10 \text{ cm}$.

▷ Paso 2 Convertir el desplazamiento a metros.

$x = 10 \text{ cm} = 0.1 \text{ m}$.

▷ Paso 3 Aplicar la fórmula de la energía potencial elástica ($U_e = \frac{1}{2}kx^2$).

$U_e = \frac{1}{2}(300 \text{ N/m})(0.1 \text{ m})^2$
$U_e = \frac{1}{2}(300 \text{ N/m})(0.01 \text{ m}^2)$
$U_e = \frac{1}{2}(3 \text{ N} \cdot \text{m}) = 1.5 \text{ J}$.

Respuesta: La energía potencial elástica almacenada es de $1.5 \text{ J}$.

Solución

▷ Paso 1 Calcular el esfuerzo ($\sigma$).

Fuerza $F = 4000 \text{ N}$.

Área $A = 1 \text{ cm}^2 = 1 \times 10^{-4} \text{ m}^2$.

$\sigma = \frac{F}{A} = \frac{4000 \text{ N}}{1 \times 10^{-4} \text{ m}^2} = 40 \times 10^6 \text{ Pa} = 40 \text{ MPa}$.

▷ Paso 2 Calcular la deformación unitaria longitudinal ($\epsilon$).

Longitud original $L_0 = 2 \text{ m}$.

Alargamiento $\Delta L = 0.4 \text{ mm} = 0.4 \times 10^{-3} \text{ m}$.

$\epsilon = \frac{\Delta L}{L_0} = \frac{0.4 \times 10^{-3} \text{ m}}{2 \text{ m}} = 0.2 \times 10^{-3} = 0.0002$.

▷ Paso 3 Aplicar la Ley de Hooke generalizada ($\sigma = E\epsilon$) y despejar $E$.

$E = \frac{\sigma}{\epsilon}$

$E = \frac{40 \times 10^6 \text{ Pa}}{0.0002} = \frac{40 \times 10^6 \text{ Pa}}{2 \times 10^{-4}} = 20 \times 10^{10} \text{ Pa} = 200 \times 10^9 \text{ Pa}$.

▷ Paso 4 Expresar el resultado en Gigapascales (GPa).

$E = 200 \text{ GPa}$.

Respuesta: El Módulo de Young del material es $200 \text{ GPa}$.

Solución

▷ Paso 1 Entender la relación gráfica.

La pendiente de la gráfica $F_{aplicada}$ vs. $x$ es la constante del resorte $k$.

▷ Paso 2 Calcular la pendiente usando el punto dado y el origen ($0,0$).

Pendiente $k = \frac{\Delta F}{\Delta x} = \frac{F_f - F_i}{x_f - x_i}$

Usando el origen ($F_i=0, x_i=0$) y el punto dado ($F_f=50 \text{ N}, x_f=0.2 \text{ m}$):

$k = \frac{50 \text{ N} - 0 \text{ N}}{0.2 \text{ m} - 0 \text{ m}} = \frac{50 \text{ N}}{0.2 \text{ m}}$.

▷ Paso 3 Calcular el valor de $k$.

$k = 250 \text{ N/m}$.

Respuesta: La constante del resorte es $250 \text{ N/m}$.

Solución

▷ Paso 1 Entender que el trabajo realizado es el cambio en la energía potencial elástica.

$W = \Delta U_e = U_{e,final} - U_{e,inicial}$.

▷ Paso 2 Calcular la energía potencial elástica inicial ($U_{e,inicial}$).

Desplazamiento inicial $x_i = 5 \text{ cm} = 0.05 \text{ m}$.

$U_{e,inicial} = \frac{1}{2}kx_i^2 = \frac{1}{2}(150 \text{ N/m})(0.05 \text{ m})^2 = \frac{1}{2}(150)(0.0025) \text{ J} = 0.1875 \text{ J}$.

▷ Paso 3 Calcular la energía potencial elástica final ($U_{e,final}$).

Desplazamiento final $x_f = 15 \text{ cm} = 0.15 \text{ m}$.

$U_{e,final} = \frac{1}{2}kx_f^2 = \frac{1}{2}(150 \text{ N/m})(0.15 \text{ m})^2 = \frac{1}{2}(150)(0.0225) \text{ J} = 1.6875 \text{ J}$.

▷ Paso 4 Calcular el trabajo realizado.

$W = U_{e,final} - U_{e,inicial} = 1.6875 \text{ J} - 0.1875 \text{ J} = 1.5 \text{ J}$.

Respuesta: El trabajo realizado para estirar el resorte entre esas dos posiciones es $1.5 \text{ J}$.

Solución

▷ Paso 1 Identificar los datos proporcionados.

Energía potencial elástica $U_e = 2.0 \text{ J}$.

Desplazamiento $x = 4.0 \text{ cm} = 0.04 \text{ m}$.

▷ Paso 2 Usar la fórmula de la energía potencial elástica y despejar $k$.

$U_e = \frac{1}{2}kx^2 \Rightarrow k = \frac{2U_e}{x^2}$.

▷ Paso 3 Sustituir los valores y calcular $k$.

$k = \frac{2(2.0 \text{ J})}{(0.04 \text{ m})^2} = \frac{4.0 \text{ J}}{0.0016 \text{ m}^2}$.

$k = 2500 \text{ N/m}$ (ya que $J = N \cdot m$).

Respuesta: La constante de rigidez del resorte es $2500 \text{ N/m}$.

Solución

▷ Paso 1 (a) Fórmula para resortes en serie.

Para resortes en serie, la inversa de la constante elástica equivalente es la suma de las inversas de las constantes individuales:

$\frac{1}{k_{eq}} = \frac{1}{k_A} + \frac{1}{k_B}$.

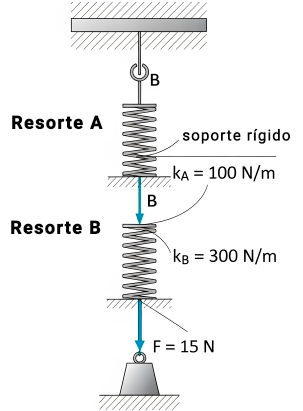
▷ Paso 2 (a) Calcular $k_{eq}$.

$\frac{1}{k_{eq}} = \frac{1}{100 \text{ N/m}} + \frac{1}{300 \text{ N/m}} = \frac{3+1}{300 \text{ N/m}} = \frac{4}{300 \text{ N/m}}$.

$k_{eq} = \frac{300 \text{ N/m}}{4} = 75 \text{ N/m}$.

▷ Paso 3 (b) Calcular el estiramiento total ($x_{total}$) del sistema.

La fuerza total aplicada al sistema es $F = 15 \text{ N}$.

$F = k_{eq} x_{total} \Rightarrow x_{total} = \frac{F}{k_{eq}}$.

$x_{total} = \frac{15 \text{ N}}{75 \text{ N/m}} = 0.2 \text{ m}$.

▷ Paso 4 (c) Calcular el estiramiento de cada resorte.

En una conexión en serie, la fuerza es la misma en cada resorte e igual a la fuerza total aplicada: $F_A = F_B = F = 15 \text{ N}$.

Estiramiento del resorte A ($x_A$):

$x_A = \frac{F_A}{k_A} = \frac{15 \text{ N}}{100 \text{ N/m}} = 0.15 \text{ m}$.

Estiramiento del resorte B ($x_B$):

$x_B = \frac{F_B}{k_B} = \frac{15 \text{ N}}{300 \text{ N/m}} = 0.05 \text{ m}$.

▷ Paso 5 (c) Verificar que la suma de los estiramientos individuales es igual al estiramiento total.

$x_A + x_B = 0.15 \text{ m} + 0.05 \text{ m} = 0.2 \text{ m}$. Esto coincide con $x_{total}$.

Respuesta:

a) La constante elástica equivalente del sistema en serie es $75 \text{ N/m}$.
b) El estiramiento total del sistema es $0.2 \text{ m}$ o $20 \text{ cm}$.
c) El resorte A se estira $0.15 \text{ m}$ ($15 \text{ cm}$) y el resorte B se estira $0.05 \text{ m}$ ($5 \text{ cm}$).

Ejercicios para Practicar de La Ley de Hooke

Para poder aprender mucho mejor este tema, te ponemos algunos ejercicios más para que puedas resolverlos en tu libreta y al final puedas comprobar tus resultados, recuerda dar click en "Ver Solución". ??

Ver Solución

Ver Solución

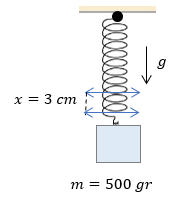
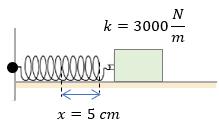
Examen de la Ley de Hooke

Llegó el momento de practicar, evalúa tus conocimientos sobre la Ley de Hooke.

Conclusión

La Ley de Hooke es un pilar en el estudio de la elasticidad, proporcionando una descripción matemática simple pero poderosa del comportamiento de los resortes y la respuesta elástica lineal de los materiales sólidos. Hemos visto cómo relaciona la fuerza con el desplazamiento en resortes a través de la constante $k$, y cómo se generaliza a la relación entre esfuerzo y deformación en materiales mediante el Módulo de Young $E$. Además, la energía almacenada debido a la deformación elástica es un concepto crucial derivado de esta ley.

Aunque la Ley de Hooke tiene sus limitaciones (es válida solo dentro del límite elástico), su comprensión es fundamental para una amplia gama de aplicaciones en ciencia e ingeniería. En los próximos artículos, continuaremos construyendo sobre estos cimientos, explorando con más detalle los diferentes módulos de elasticidad y el comportamiento de los materiales más allá de la región lineal.

Ejercicios resueltos, ¿tienes dudas? Hazlas en la caja de comentarios abajo, y si te gustó y te ayudó... 🙂

Por favor comparte, y ayúdanos a alfabetizar de manera científica a más personas 😎