Solución Problema 1 de la Ley de Hooke

Vamos a resolver el ejercicio propuesto para reforzar los conocimientos adquiridos en el tema de La ley de Hooke en el área de Elasticidad, con este ejemplo resuelto el alumno podrá corroborar su respuesta y verificar si ha llegado al mismo resultado.

Nivel de Dificultad: ⭐⭐

Problema 4. Cuando una masa de 500 gr cuelga de un resorte, este se alarga 3 cm ¿cuál es la constante elástica?

Problema de la ley de Hooke

Solución:

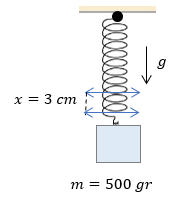
Lo primero que tenemos que ver en un problema de la Ley de Hooke, es siempre verificar si la masa cuelga de algún lado o si el resorte permanece totalmente horizontal, ¿por qué?, porque cuando el resorte está en posición vertical junto con la masa, entonces tenemos qué hacer uso del peso, e involucrar a la fórmula del peso basada en la segunda ley de Newton

Calcular la constante elástica

Datos:

$\displaystyle x=3cm$

$\displaystyle m=500gr$

a) Obteniendo la constante elástica

Como bien sabemos, al tener el resorte de forma vertical, la gravedad se ve involucrada en el cálculo de la fuerza o peso. Entonces lo primero que haremos será convertir nuestras unidades en las unidades del SI "Sistema Internacional", de tal forma que:

$\displaystyle x=3cm\left( \frac{1m}{100cm} \right)=0.03m$

Y hacemos lo mismo con la masa del bloque:

$\displaystyle m=500gr\left( \frac{1kg}{1000gr} \right)=0.5kg$

Bien, ahora vemos la fórmula de la ley de hooke

$\displaystyle F=kx$

Como es la constante la que necesitamos, entonces la despejamos de la fórmula, quedando así:

$\displaystyle k=\frac{F}{x}$

Pero la fuerza es igual que el peso, esto es por la segunda ley de newton:

$\displaystyle k=\frac{F}{x}=\frac{mg}{x}$

$\displaystyle k=\frac{mg}{x}$

Sustituyendo nuestros datos en la fórmula:

$\displaystyle k=\frac{mg}{x}=\frac{\left( 0.5kg \right)\left( 9.8\frac{m}{{{s}^{2}}} \right)}{0.03m}=163.33\frac{N}{m}$

Es decir que la constante elástica del resorte es de 163.33 Newtons

Resultado:

$\displaystyle k=163.33\frac{N}{m}$

3 Comentarios Publicados

lucia dice:

23 mayo, 2023 a las 11:39 am

buenas estoy en 3 eso, ¿podria hacermelo mas sencillo? gracias

Responder
1. Laura dice:
  
  3 noviembre, 2023 a las 9:28 am
  
  Gracias fue de mucha ayuda
  
  Responder
maria ines zurita dice:

14 junio, 2023 a las 9:41 pm

muy bien explicado, excelente material, ojalá tengan un ppt.

Responder

Deja una respuesta Cancelar la respuesta