Segunda Ley de Newton - Ejercicios Resueltos

¿Qué tal lectores? Antes de comenzar a ver ejercicios resueltos de la segunda ley de Newton, es importante haber leído Las tres leyes de Newton (Click aquí para leer el post)  ya que a partir de la teoría explicada en ese artículo, vamos a poder entender con profundidad los ejemplos resueltos y no tendremos ninguna dificultad, así que si ya leíste las tres leyes, entonces es momento de practicar y poner a prueba nuestros conocimientos. 😎

Ten siempre en cuenta que el fundamento teório es esencial para comprender a profundidad el como interactúan las fuerzas, la masa, y la aceleración en distintos contextos. Vamos a conectar con ejercicios de fuerzas de fricción. ¿Cómo afecta el movimiento de un objeto en contacto con superficies rugosas?, sobre plano inclinado donde veremos como descomponer fuerzas y calcular el movimiento de objetos en pendientes, así como el peso y la fuerza neta. ¿Cómo influye la gravedad en el peso de los cuerpos y cómo determinar la fuerza total aplicada?.

Fórmula de la Segunda Ley de Newton

Si bien la segunda Ley de Newton nos advierte, que la fuerza F que actúa en un cuerpo es directamente proporcional a la aceleración y a la masa. Y la escribíamos matemáticamente mediante la siguiente fórmula:

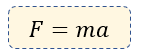
$\displaystyle \overrightarrow{F}=m\overrightarrow{a}$

De aquí podemos decir que entre mayor sea la masa de un cuerpo, tanto mayor será su inercia; es decir, la masa de un cuerpo es una medida de la inercia del mismo.

Dónde:

F = Magnitud de la fuerza aplicada a un cuerpo (N)

m = Masa del cuerpo (kg)

a = Magnitud de la aceleración que recibe el cuerpo (m/s²)

Fórmula para calcular el Peso de un objeto

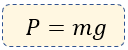
Dónde:

P = Magnitud del peso del cuerpo (N)

m = Masa del cuerpo (kg)

g = Magnitud de la aceleración de la gravedad (m/s²)

Tanto la fórmula de la segunda Ley de Newton como la del peso son exactamente la misma, el peso de un cuerpo representa la magnitud de la fuerza con que la tierra atrae a la masa de un cuerpo.

Ejercicios Resueltos de la Segunda Ley de Newton

Empecemos con los ejemplos resueltos de ésta segunda ley, estos problemas bien pueden ser para un nivel de secundaria o preparatoria, ESO, etc... Veamos entonces.

Solución: En el ejemplo, tenemos prácticamente nuestros datos, que es lo primero que tenemos que hacer.

F = 50 N

m = 13,000 gramos

a = ?

Hacemos la conversión de los gramos a kilogramos, ya que son las unidades del sistema internacional.

$\displaystyle m=13000g\left( \frac{1kg}{1000g} \right)=13kg$

Despejando la aceleración de la fórmula de la segunda ley de Newton, tenemos:

$\displaystyle a=\frac{F}{m}=\frac{50N}{13kg}=3.85\frac{m}{{{s}^{2}}}$

Que vendría a ser nuestro resultado.

Solución: Hacemos lo mismo del paso anterior, vamos a colocar nuestros datos, con ello tenemos entonces:

F = 350 N

a = 520 cm/s^2

m = ?

Vamos a colocar a nuestra aceleración en unidades de metros por segundo al cuadrado, para ello hacemos nuestra conversión.

$\displaystyle a=520\frac{cm}{{{s}^{2}}}\left( \frac{1m}{100cm} \right)=5.2\frac{m}{{{s}^{2}}}$

Ahora si podemos despejar a la masa de la fórmula de Newton.

$\displaystyle m=\frac{F}{a}=\frac{350N}{5.2\frac{m}{{{s}^{2}}}}=67.31kg$

Solución: Pasamos a escribir los datos:

m = 45 kg

a = 5m/s^2

F = ?

Entonces aplicamos la fórmula de la segunda Ley de Newton

$\displaystyle F=ma=(45kg)(5\frac{m}{{{s}^{2}}})=225N$

Qué vendría a ser nuestra fuerza.

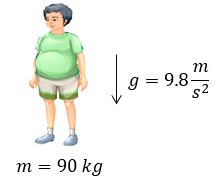
Solución:

Para poder encontrar el peso de una persona, tenemos que recurrir a nuestra fórmula de la segunda ley de newton pero en términos del peso, es decir:

$\displaystyle P=mg$

los datos que tenemos son:

$\displaystyle m=90kg$

$\displaystyle g=9.8\frac{m}{{{s}^{2}}}$

Teniendo en cuenta los datos, solo basta sustituir los datos en la fórmula:

$\displaystyle P=mg=(90kg)(9.8\frac{m}{{{s}^{2}}})=882N$

Es decir que el peso de la persona es de 882 Newtons.

Solución:

Lo primero que haremos será convertir la masa a kilogramos:

$\displaystyle m=2500g\left( {\frac{{1kg}}{{1000g}}} \right)=2.5kg$

Aplicamos la fórmula de la aceleración:

$\displaystyle a=\frac{F}{m}=\frac{{15\frac{m}{{{{s}^{2}}}}}}{{2.5kg}}=6\frac{m}{{{{s}^{2}}}}$

Por lo tanto la aceleración del objeto será de 6 m/s²

Solución:

Lo primero que haremos será determinar la componente de fuerza gravitacional paralela al plano:

$\displaystyle {{F}_{{paralela}}}=m\cdot g\cdot sen\theta $

Dónde: g = 9.8 m/s² y θ = 30°

Sustituimos valores:

$\displaystyle {{F}_{{paralela}}}=\left( {10kg} \right)\left( {9.8\frac{m}{{{{s}^{2}}}}} \right)\left( {sen30{}^\circ } \right)=49N$

Por lo que la fuerza neta, sería:

$\displaystyle {{F}_{{Neta}}}=49N$

Solución:

Aplicaremos la fórmula del peso, que prácticamente es parte de la 2da Ley de Newton:

$\displaystyle P=m\cdot g$

Sustituyendo los valores del peso:

$\displaystyle P=\left( {15kg} \right)\cdot \left( {3.7\frac{m}{{{{s}^{2}}}}} \right)=55.5N$

Por lo que obtendríamos un peso en marte de 55.5 Newtons

Solución:

Vamos a calcular la fuerza de fricción con la siguiente fórmula:

$\displaystyle {{F}_{{friccion}}}={{\mu }_{k}}\cdot m\cdot g$

Sustituyendo nuestros datos en la fórmula:

$\displaystyle {{F}_{{friccion}}}=\left( {0.3} \right)\left( {20kg} \right)\left( {9.8\frac{m}{{{{s}^{2}}}}} \right)=58.8N$

Determinando la fuerza neta:

$\displaystyle {{F}_{{neta}}}={{F}_{{aplicada}}}-{{F}_{{friccion}}}$

Sustituimos:

$\displaystyle {{F}_{{neta}}}=120N-58.8N=61.2N$

Ahora, calculamos la aceleración:

$\displaystyle a=\frac{{{{F}_{{neta}}}}}{m}=\frac{{61.2N}}{{20kg}}=3.06\frac{m}{{{{s}^{2}}}}$

Por lo que la aceleración del bloque es de 3.06 m/s²

Solución:

Primero calcularemos la masa total del sistema:

$\displaystyle {{m}_{{total}}}={{m}_{A}}+{{m}_{B}}=5+8=13kg$

Usamos la fórmula de la aceleración:

$\displaystyle a=\frac{{{{F}_{{aplicada}}}}}{{{{m}_{{total}}}}}$

Sustituyendo:

$\displaystyle a=\frac{{50N}}{{13kg}}\approx 3.85\frac{m}{{{{s}^{2}}}}$

Por lo que la aceleración del sistema será de 3.85 m/s²

Solución:

Vamos a calcular la fuerza neta:

$\displaystyle {{F}_{{neta}}}={{F}_{{aplicada}}}-{{F}_{{friccion}}}$

Sustituyendo:

$\displaystyle {{F}_{{neta}}}=100-40=60N$

Determinamos la aceleración en $\displaystyle \frac{m}{{{{s}^{2}}}}$

$\displaystyle a=\frac{{{{F}_{{neta}}}}}{m}=\frac{{60N}}{{20kg}}=3\frac{m}{{{{s}^{2}}}}$

Sin embargo el problema nos pide convertir la aceleración a kilometros sobre horas al cuadrado. Entonces haremos la conversión de unidades.

$\displaystyle a=3\frac{m}{{{{s}^{2}}}}\left( {\frac{{1km}}{{1000m}}} \right)\left( {\frac{{3600s}}{{1hr}}} \right)\left( {\frac{{3600s}}{{1hr}}} \right)=38,880\frac{{km}}{{h{{r}^{2}}}}$

Lo que sería nuestra aceleración 38,880 km/hr²

Solución:

Procedemos a calcular la fuerza paralela al plano:

$\displaystyle {{F}_{{paralela}}}=m\cdot g\cdot sen\theta $

Sustituyendo los valores que tenemos:

$\displaystyle {{F}_{{paralela}}}=\left( {15kg} \right)\left( {9.8\frac{m}{{{{s}^{2}}}}} \right)sen45{}^\circ \approx 103.99N$

Ahora procedamos a calcular la fuerza de fricción:

$\displaystyle {{F}_{{friccion}}}={{\mu }_{k}}\cdot m\cdot g\cdot \cos \theta $

Por lo que nuestra fricción será:

$\displaystyle {{F}_{{friccion}}}=\left( {0.2} \right)\left( {15kg} \right)\left( {9.8\frac{m}{{{{s}^{2}}}}} \right)\cos 45{}^\circ \approx 20.8N$

Ahora si, calculamos la fuerza neta:

$\displaystyle {{F}_{{neta}}}={{F}_{{paralela}}}-{{F}_{{friccion}}}=103.99N-20.8\approx 83.19N$

Por lo que la fuerza neta que actúa sobre el bloque es de 83.19 Newtons

Ejercicios para Practicar de la Segunda Ley de Newton

Ahora es momento de practicar, y que finalmente puedas ver los resultados explicados paso a paso para corroborar si has obtenido la respuesta correcta ??

? Ver Solución

? Ver Solución

? Ver Solución

Examen de la Segunda Ley de Newton

Llegó el momento de poner a prueba tus habilidades sobre esta ley tan importante en la física. ¡Buena suerte! 😀