Solución Problema 3 Segunda Ley de Newton

Con este último problema de la Segunda ley de Newton, el alumno finalmente refuerza el uso de la fórmula utilizando los despejes de la fórmula, ir viendo las diversas variables que se pueden obtener a través de la segunda ley de newton y que resuelve todo tipo de problemas que se puede encontrar en algún examen o tarea. 😊👇

Nivel de Dificultad: ⭐⭐⭐

Problema 7. Calcular la magnitud de la aceleración que recibirá el siguiente bloque como resultado de las fuerzas aplicadas

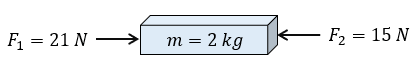
Segunda Ley de Newton problemas

Solución:

Este tipo de problemas son más interesantes porque se comprende la aplicación de suma de fuerzas, en la imagen observamos que existen dos fuerzas (una en dirección a la derecha) y otra en (dirección a la izquierda), si observa, la primera fuerza es de 21 Newtons y la segunda de 15 Newtons, al someterse al bloque de madera de 2kg, en oposición a las fuerzas obtendremos una fuerza resultante.

Obtener la aceleración del bloque

Datos:

$\displaystyle {{F}_{1}}=21N$

$\displaystyle {{F}_{2}}=15N$

$\displaystyle m=2kg$

a) Obtener la aceleración del bloque

Al tener dos fuerzas interactuando en el bloque, lo primero que haremos será encontrar esa fuerza resultante.

$\displaystyle {{F}_{R}}={{F}_{1}}-{{F}_{2}}$

La fuerza que va hacía la derecha (es positiva) y la fuerza que va hacía la izquierda (es negativa). Esto es con el fin de establecer un sistema de referencia de fuerzas, puede leer más de esto en la Primera Condición de Equilibrio.

Sustituyendo las fuerzas, obtenemos la fuerza resultante:

$\displaystyle {{F}_{R}}={{F}_{1}}-{{F}_{2}}=21N-15N=6N$

Una vez que tenemos la fuerza neta, ahora si podemos usar la fórmula.

$\displaystyle F=ma$

Despejando a la aceleración "a", obtenemos:

$\displaystyle a=\frac{F}{m}$

Recordar que a la fuerza a la que nos referimos es a la fuerza resultante, entonces:

$\displaystyle a=\frac{{{F}_{R}}}{m}=\frac{6N}{2kg}=3\frac{m}{s}$

Por lo que la aceleración para mover al bloque debe ser de 3 m/s²

Resultado:

$\displaystyle a=3\frac{m}{s}$

2 Comentarios Publicados

Briggeth kohen dice:

2 agosto, 2023 a las 3:01 pm

Ayudarme en todos los ejercicios de Newton

Responder
J Jaime Ibarra dice:

12 agosto, 2023 a las 8:18 am

Excelente información para los alumnos q comienzan con sus clases de Dinámica. Muchas gracias por su valiosa aportación

Responder

Deja una respuesta Cancelar la respuesta