Primera Condición de Equilibrio - Ejercicios Resueltos

En estática es importante conocer las dos condiciones de equilibrio más importantes para comprender gran parte de la mecánica en Física. Y aunque se suele estudiar en niveles universitarios de ingeniería o la licenciatura pura en Física y Matemáticas, en nuestro paso como estudiantes también nos toca lidiar con estos tipos de problemas, es por eso que este post será más práctico que teórico, vamos a explicar paso a paso los ejercicios para que los puedas comprender en su totalidad. 😀

🤔 ¿Qué es la primera condición de equilibrio?

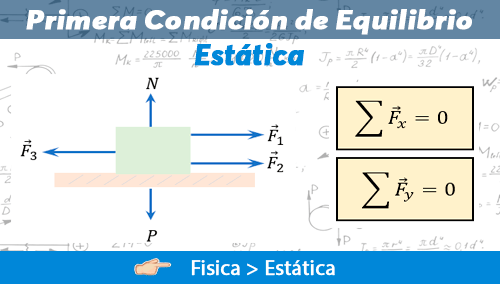
En física para que un cuerpo sea considerado en equilibrio la fuerza neta o toda la resultante de todas las fuerzas que actúan sobre él, deben ser igual a cero. Viéndolo de otra forma, es como decir que la suma vectorial tanto en el eje "x", como en el eje "y" deben sumar 0.  Es importante que en este punto domines muy bien la descomposición vectorial en su forma rectangular, tal como se explico el método del polígono de forma analítica en el tema de vectores.

• Descomponer vectores en su forma rectangular

Con esto podemos establecer entonces que:

En términos matemáticos esto es:

$\displaystyle \sum{{{{\vec{F}}}_{x}}=0}$

$\displaystyle \sum{{{{\vec{F}}}_{y}}=0}$

Algunos ejemplos de equilibrio de traslación

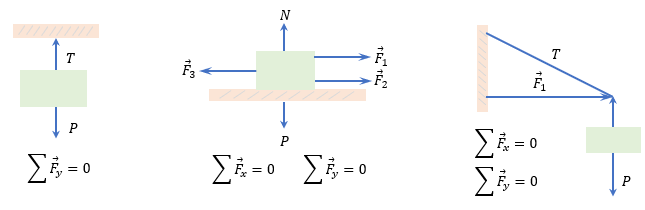
🖼 Diagrama de Cuerpo libre

Es muy difícil resolver un problema de estática si no se traza un diagrama de cuerpo libre del problema, con el DCL (Diagrama de Cuerpo Libre) podemos aislar un cuerpo y exportarlo a un plano cartesiano para analizar las fuerzas que actúan sobre dicho cuerpo.

Los pasos para trazar un diagrama de cuerpo libre, son los siguientes:

Paso 1: Excluya el cuerpo del problema y trace todas las fuerzas que actúan sobre él, con ello podemos obtener una referencia de inicio importante para la solución de nuestro problema.

Paso 2: Dicho sistema de referencia se trazará sobre un plano cartesiano y se procederá con una descomposición de los vectores en su forma rectangular.

Paso 3: Coloque adecuadamente las fuerzas ya descompuestas, así como también los ángulos.

Paso 4: Aplique las ecuaciones de condición de equilibrio, para obtener las incógnitas deseadas.

Ahora es momento de resolver algunos ejercicios.

📄 Ejercicios Resueltos de la Primera Condición de Equilibrio

Veamos el siguiente ejercicio para la ley de equilibrio.

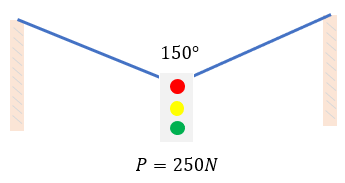
Solución:

Elaboramos el diagrama de cuerpo libre de nuestro problema, extrayendo primero las fuerzas que están activas en dicho cuerpo, incluyendo los ángulos.

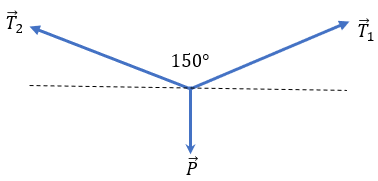
Como los cables están generando una tensión con los postes que soportan al semáforo, van en dirección a los postes, no al semáforo. El peso del semáforo hace que la fuerza jale hacía abajo. Una vez teniendo en cuenta dicho punto, es momento de realizar un diagrama de cuerpo libre más completo, colocando las fuerzas en el plano cartesiano.

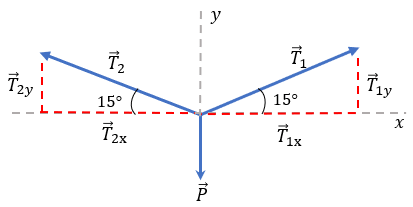
Hemos colocado 15° en los ángulos de las tensiones con la horizontal, ya que el ángulo que había entre cable y cable eran de 150°. Es lógico que los ángulos restantes fueran 30°, ahora vamos a colocar la sumatoria de fuerzas en el eje "x"

$\displaystyle \sum{{{{\vec{F}}}_{x}}}=0$

Observamos por nuestro plano cartesiano, que solamente lo que está de lado derecho es positivo, y de lado izquierdo negativo.

Para el eje "x"

$\displaystyle \sum{{{\overrightarrow{F}}_{x}}}={{\overrightarrow{T}}_{1}}_{x}-{{\overrightarrow{T}}_{2}}_{x}=0$

Para el eje "y"

$\displaystyle \sum{{{\overrightarrow{F}}_{y}}}={{\overrightarrow{T}}_{1}}_{y}+{{\overrightarrow{T}}_{2}}_{y}-P=0$

Resolviendo para el eje "x"

Como bien sabemos, tenemos que descomponer nuestros vectores en su forma rectangular de tal forma que:

$\displaystyle \sum{{{\overrightarrow{F}}_{x}}}={{T}_{1}}\cos 15{}^\circ -{{T}_{2}}\cos 15{}^\circ =0$

Al tratarse de una igualdad, vamos a despejar de tal forma que nos quede así:

$\displaystyle {{T}_{1}}\cos 15{}^\circ ={{T}_{2}}\cos 15{}^\circ $

$\displaystyle {{T}_{1}}={{T}_{2}}$

Esto nos da entender, que tanto la tensión 1 como la tensión 2, son iguales. Ahora lo que necesitamos saber es cuanto vale la tensión, y ese dato nos arrojará cuando resolvamos para el eje "y".

Resolviendo para el eje "y"

$\displaystyle {{T}_{1}}sen15{}^\circ +{{T}_{2}}sen15{}^\circ -250N=0$

$\displaystyle {{T}_{1}}sen15{}^\circ +{{T}_{2}}sen15{}^\circ =250N$

Pero como sabemos que:

$\displaystyle {{T}_{1}}={{T}_{2}}$

$\displaystyle {{T}_{1}}sen15{}^\circ +{{T}_{1}}sen15{}^\circ =250N$

Es decir:

$\displaystyle 2{{T}_{1}}sen15{}^\circ =250N$

Despejando a T1

$\displaystyle {{T}_{1}}=\frac{250N}{2sen15{}^\circ }=482.96N$

Esto quiere decir que tanto T1 como T2 tienen una fuerza de tensión de 482.96 Newtons cada una.

Resultado:

$\displaystyle {{T}_{1}}={{T}_{2}}=482.96N$