Teorema de Lamy - Ejercicios Resueltos

El teorema de Lamy o Lami es un teorema que se asocia a las magnitudes de las fuerzas que son coplanares, concurrentes y no colineales que mantienen el equilibrio de un objeto. El teorema de Lami se puede utilizar para resolver muchos problemas de la vida real, y muy importante en física. En especial en el área de la mecánica-estática o estructural.

El teorema de Lamy es en honor al matemático francés Bernard Lami (16445 – 1716).

¿Qué nos dice el Teorema de Lamy?

El teorema de Lami establece que, si tres fuerzas coplanares que actúan en un punto están en equilibrio, entonces cada fuerza es proporcional al seno el ángulo formado entre ellas. Veamos la imagen de abajo.

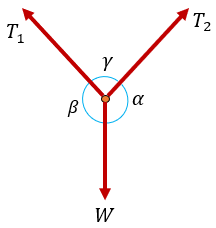
Donde T1, T2, y W son las fuerzas coplanares que actúan en un punto, es normal que podamos ver en otras páginas o libros la representación por fuerzas en vez de tensiones y es lo mismo, recordar que la tensión, fuerza y peso son lo mismo.

¿Cuál es la fórmula del teorema de Lamy?

Pues bien, la fórmula del teorema de Lami o Lamy, es la siguiente:

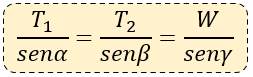
Prestar atención a la imagen de las tensiones 1 y 2, y el peso que se puso más arriba, para entende a que refiere cada pate.

Ejercicios Resueltos del Teorema de Lamy

Es momento de realizar algunos ejercicios para comprender un poco mejor este teorema de Lamy

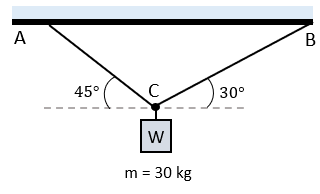
Solución:

Realizaremos un diagrama de cuerpo libre sobre el problema, per antes debemos calcular el peso del bloque de hierro.

$\displaystyle W=mg=(30kg)(9.8\frac{m}{{{{s}^{2}}}})=294N$

Ahora coloquemos nuestro diagrama de cuerpo libre

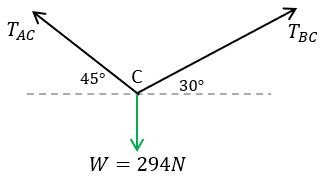
Obtenemos los ángulos requeridos para aplicar el teorema de Lamy

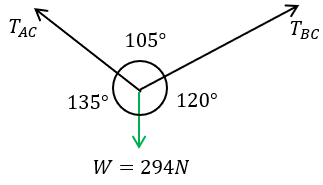
Podemos obtener primero una Tensión y después la otra, así empezaremos por encontrar a la tensión AC

$\displaystyle \frac{{{{T}_{{AC}}}}}{{sen120{}^\circ }}=\frac{W}{{sen105{}^\circ }}$

$\displaystyle \frac{{{{T}_{{AC}}}}}{{sen120{}^\circ }}=\frac{{294N}}{{sen105{}^\circ }}$

Despejando:

$\displaystyle {{T}_{{AC}}}=\frac{{\left( {294N} \right)\left( {sen120{}^\circ } \right)}}{{sen105{}^\circ }}$

$\displaystyle {{T}_{{AC}}}=\frac{{\left( {294N} \right)\left( {sen120{}^\circ } \right)}}{{sen105{}^\circ }}=263.59N$

Por lo que la Tensión AC = 263.59 N

Ahora calculemos la tensión BC

$\displaystyle \frac{{{{T}_{{BC}}}}}{{sen135{}^\circ }}=\frac{W}{{sen105{}^\circ }}$

$\displaystyle \frac{{{{T}_{{BC}}}}}{{sen135{}^\circ }}=\frac{{294N}}{{sen105{}^\circ }}$

Despejando:

$\displaystyle {{T}_{{BC}}}=\frac{{\left( {294N} \right)\left( {sen135{}^\circ } \right)}}{{sen105{}^\circ }}$

$\displaystyle {{T}_{{BC}}}=\frac{{\left( {294N} \right)\left( {sen135{}^\circ } \right)}}{{sen105{}^\circ }}=215.22N$

Por lo que la Tensión BC = 215.22 N

Entonces, las tensiones requeridas a lo largo de las direcciones mostradas son 263.59 N y 215.22 N respectivamente.

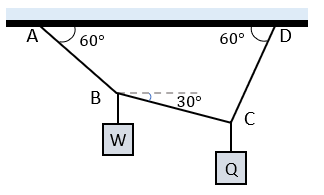
Solución:

A diferencia del primer problema, en este caso vemos un problema de equilibrio con más incógnitas, pues para saber el valor de Q, forzosamente necesitamos saber que ocurre en el punto A, y punto B, ya que si sabemos cuanto pesa el bloque W, entonces vamos a enfocarnos en esa parte.

Realizando el diagrama de cuerpo libre, obtenemos:

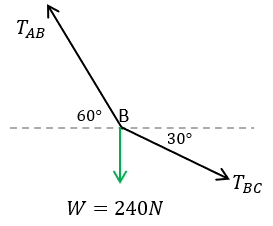
Por ángulos alternos e internos, podemos ver que la tensión AB, tiene un ángulo de 60° que junto al peso "W", forman 90° más, es decir 150°, y también observamos que de la tensión AB a la tensión BC según las manecillas del reloj, se suman también 150°, quedando así 60° entre la tensión BC y el peso, es decir:

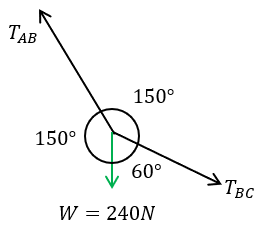
Para este problema, nos piden encontrar el valor de "Q", por lo que lo único que nos importa, es la tensión que se relaciona con "Q", en este caso sería la tensión BC, aplicando el teorema de Lamy:

$\displaystyle \frac{{{{T}_{{BC}}}}}{{sen150{}^\circ }}=\frac{W}{{sen150{}^\circ }}$

$\displaystyle \frac{{{{T}_{{BC}}}}}{{sen150{}^\circ }}=\frac{{240N}}{{sen150{}^\circ }}$

Despejando:

$\displaystyle {{T}_{{BC}}}=\frac{{\left( {240N} \right)\left( {sen150{}^\circ } \right)}}{{sen150{}^\circ }}$

Esto da como resultado:

$\displaystyle {{T}_{{BC}}}=\frac{{\left( {240N} \right)\left( {sen150{}^\circ } \right)}}{{sen150{}^\circ }}=240N$

Por lo que la tensión BC es de 240 N

Ahora analizemos el otro extremo, donde se encuentra "Q"

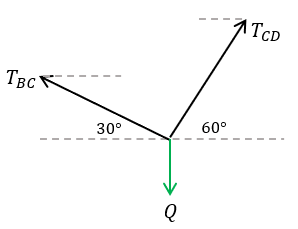
Nuevamente, por ángulos alternos internos, nos queda como arriba. Es muy fácil sumar los ángulos restantes, por lo que obtenemos lo siguiente:

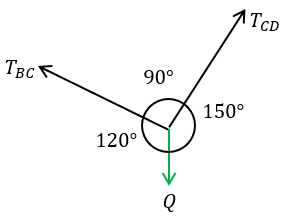
Ahora si podemos aplicar el teorema de Lamy, para encontrar el valor de "Q"

$\displaystyle \frac{Q}{{sen90{}^\circ }}=\frac{{{{T}_{{BC}}}}}{{sen150{}^\circ }}$

Recordar que la tensión BC, la calculamos en pasos anteriores:

Despejando:

$\displaystyle Q=\frac{{\left( {{{T}_{{BC}}}} \right)sen90{}^\circ }}{{sen150{}^\circ }}$

$\displaystyle Q=\frac{{\left( {240N} \right)sen90{}^\circ }}{{sen150{}^\circ }}$

Esto da como resultado:

$\displaystyle Q=\frac{{\left( {240N} \right)sen90{}^\circ }}{{sen150{}^\circ }}=480N$

El valor de Q = 480 N

y con esto terminamos este problema 😀

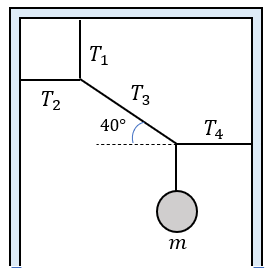
Solución:

Hasta este punto, el estudiante debe tener mayor control y dominio sobre el tema, por lo que los pasos se harán más resumidos para llegar al resultado.

Calculamos el peso de la bola de acero:

$\displaystyle W=mg=\left( {100kg} \right)\left( {9.8\frac{m}{{{{s}^{2}}}}} \right)=980N$

Ahora vamos analizar las tensiones 3 y 4, junto con el peso mediante un diagrama de cuerpo libre:

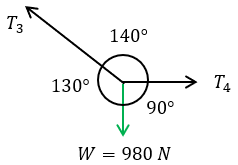
En base a ello podemos construir el teorema de Lamy:

$\displaystyle \frac{{{{T}_{3}}}}{{sen90{}^\circ }}=\frac{W}{{sen140{}^\circ }}=\frac{{{{T}_{4}}}}{{sen130{}^\circ }}$

Para ello vamos a utilizar solo la referencia del peso, para encontrar T3 y después T4

$\displaystyle \frac{{{{T}_{3}}}}{{sen90{}^\circ }}=\frac{W}{{sen140{}^\circ }}$

Sustituyendo datos y despejando:

$\displaystyle {{T}_{3}}=\frac{{\left( {980N} \right)\left( {sen90{}^\circ } \right)}}{{sen140{}^\circ }}=1524.61N$

Es decir:

Para encontrar la tensión 4, la podemos hacer a partir de la siguiente igualdad:

$\displaystyle \frac{{{{T}_{4}}}}{{sen130{}^\circ }}=\frac{W}{{sen140{}^\circ }}$

Despejando a T4

$\displaystyle {{T}_{4}}=\frac{{\left( {980N} \right)sen130{}^\circ }}{{sen140{}^\circ }}$

Esto da:

$\displaystyle {{T}_{4}}=\frac{{\left( {980N} \right)sen130{}^\circ }}{{sen140{}^\circ }}=1167.92N$

Es decir:

Hasta este punto hemos calculado las tensiones 3 y 4, para poder continuar encontrando las demas tensiones, necesitamos realizar otro diagrama de cuerpo libre y aplicar el teorema de Lamy:

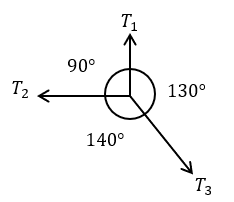
De aquí podemos aplicar el teorema de Lamy quedando así:

$\displaystyle \frac{{{{T}_{1}}}}{{sen140{}^\circ }}=\frac{{{{T}_{3}}}}{{sen90{}^\circ }}=\frac{{{{T}_{2}}}}{{sen130{}^\circ }}$

Encontrando primero a T1, nos quedamos con la siguiente parte de la igualdad

$\displaystyle \frac{{{{T}_{1}}}}{{sen140{}^\circ }}=\frac{{{{T}_{3}}}}{{sen90{}^\circ }}$

Despejando a T1:

$\displaystyle {{T}_{1}}=\frac{{{{T}_{3}}sen140{}^\circ }}{{sen90{}^\circ }}$

$\displaystyle {{T}_{1}}=\frac{{\left( {1524.61} \right)sen140{}^\circ }}{{sen90{}^\circ }}=980N$

Es decir:

Ahora, el único que nos falta será T2:

$\displaystyle {{T}_{2}}=\frac{{{{T}_{3}}sen130{}^\circ }}{{sen90{}^\circ }}$

$\displaystyle {{T}_{2}}=\frac{{\left( {1524.61N} \right)sen130{}^\circ }}{{sen90{}^\circ }}$

$\displaystyle {{T}_{2}}=\frac{{\left( {1524.61N} \right)sen130{}^\circ }}{{sen90{}^\circ }}=1167.92N$

Es decir:

Y con esto terminamos los ejemplos resueltos del teorema de Lamy