Segunda Condición de Equilibrio - Ejercicios Resueltos

Hasta este punto es muy seguro que ya estudiaste la primera condición de equilibrio, un tema muy importante en la estática. Y que después de comprender dicha condición es necesaria conocer la segunda condición de equilibrio, dicha condición se genera cuando dicho movimiento está girando sobre su mismo eje.

🤔 ¿Qué es la segunda condición de equilibrio?

Para entender la segunda condición de equilibrio, debemos recordar el principio de la primera condición, es decir. Así como un cuerpo puede permanecer en equilibrio de traslación si la resultante de fuerzas que actúan sobre dicho cuerpo es cero, lo mismo ocurre cuando un cuerpo está girando sobre su mismo eje.

Matemáticamente lo podríamos escribir así:

$\displaystyle \sum{\overrightarrow{M}}=0$

Algunos ejemplos de equilibrio de rotación.

👉 ¿Qué es un Par de Fuerzas?

Para la segunda condición de equilibrio, es importante conocer la definición de par de fuerzas , puesto que con este concepto se irán trabajando todos los ejercicios.

Se puede observar el ejemplo, en un disco sometido a un par de fuerzas .

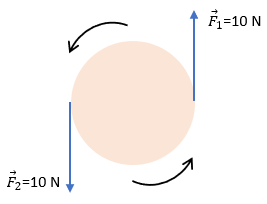
Si deseamos encontrar la fuerza resultante en el disco, bastaría con observar el sentido de dicho para de fuerzas. La fuerza F1 va hacía arriba lo que consideramos como positivo (+), mientras que la fuerza 2 F2 va en dirección contraria, lo que consideraríamos como (-). Lo que nos daría el valor de cero. Es decir, el disco no se mueve.

✅ ¿Qué es un Momento? o ¿Qué es un Torque?

Muchas veces escucharemos el término de Momento, Torque e inclusive también a Momento de Torsión, ambos términos son lo mismo, y dicha definición radica en aquella fuerza capaz de hacer girar un cuerpo.

Sin embargo dicha definición también incluye una ecuación o fórmula matemática importante.

$\displaystyle M=Fd$

Dónde:

M = Momento de una fuerza

F = Fuerza aplicada

d = Distancia (brazo de palanca)

El momento se mide en unidades de (Nm)

Nota: Algunos libros le colocan a la distancia "d" la letra "r", lo qué también es correcto.

Aunque es un tema esencial para comprender la estática, es importante que se estudie los casos que podemos encontrarnos al calcular los momentos. Veamos 4 casos comunes.

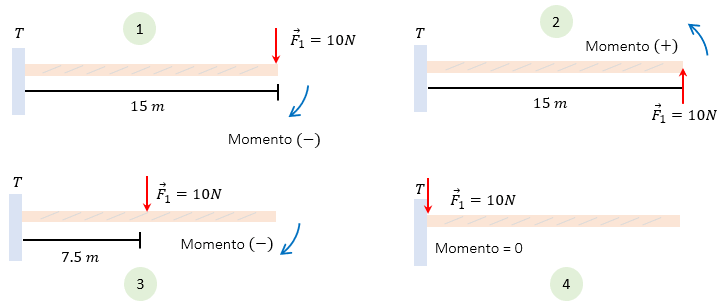
De los cuatro casos aquí expuestos, podemos aprender mucho con analizar cada uno de ellos. Por ejemplo debemos de tomar en cuenta lo siguiente:

• El momento aplicado tiene que partir de un punto en común, en estos ejemplos todos toman un punto de apoyo que llamaremos T
• En el caso 1 y 2 la viga es sometida a fuerzas iguales pero con diferente sentido, además la distancia también es la misma.
• En el caso 3, a pesar de que la fuerza es la misma, el brazo de palanca o "distancia" se toma realiza a la mitad.

Teniendo en cuenta estos puntos, vamos a puntualizar otro punto importante.

Si deseamos encontrar el Momento de cada fuerza lo haríamos de la siguiente forma:

Caso 1:

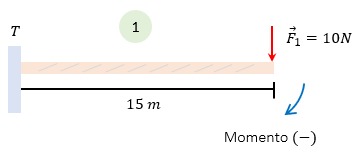
Para este caso, basta con observar el brazo de palanca que existe desde donde está la fuerza hasta el punto de apoyo T , hay 15 metros y además una fuerza de 10N, considerando que un momento es positivo si la fuerza apunta en dirección contraria a las manecillas del reloj, y negativo si gira en dirección horaria, entonces sabremos que es un momento negativo.

$\displaystyle \sum{\overrightarrow{M}}=Fd=\left( -10N \right)\left( 15m \right)=-150Nm$

Caso 2: 

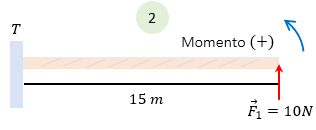
La única diferencia del caso 1, es que la fuerza está en dirección contraria a las manecillas del reloj, por lo que tendremos un momento positivo. Esto es matemáticamente:

$\displaystyle \sum{\overrightarrow{M}}=Fd=\left( 10N \right)\left( 15m \right)=150Nm$

Caso 3:

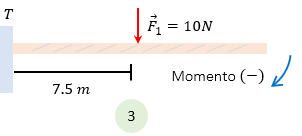
En el caso 3, vemos claramente que la fuerza está en dirección de las manecillas del reloj, por lo cual es negativa, y la distancia donde se aplica la fuerza es a mitad del punto de apoyo T, entonces decimos que:

$\displaystyle \sum{\overrightarrow{M}}=Fd=\left( -10N \right)\left( 7.5m \right)=75Nm$

Caso 4: 

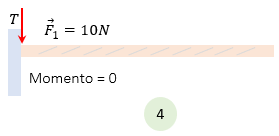
Este caso es importante, al no haber ningún brazo de palanca "distancia" es lógico que la viga no tendrá ninguna reacción de fuerza, ya que está justamente en el punto de apoyo, ahora matemáticamente podríamos explicarlo así:

$\displaystyle \sum{\overrightarrow{M}}=Fd=\left( 10N \right)\left( 0m \right)=0$