Plano Inclinado - Ejercicios Resueltos

En física existe una de las aplicaciones de las leyes de Newton para poder resolver problemas del tipo de plano inclinado, un plano inclinado son un tipo de ejercicios comúnmente encontrados en los libros de física, donde se analiza el movimiento de objetos que se desplazan sobre una superficie inclinada. Estos problemas involucran la aplicación de conceptos como la fuerza, el trabajo, la energía y la cinemática para comprender cómo los objetos se comportan cuando están sujetos a la gravedad y se mueven a lo largo de una superficie inclinada.

Es importante que en este punto de aplicación, se tenga conocimiento del uso del álgebra y la trigonometría para encontrar la cantidad física faltante.

Pasos para resolver un problema de Plano Inclinado

Para resolver problemas de plano inclinado debemos de considerar alguna serie de pasos sistemáticos y aplicar los principios de la física, por lo que debemos tener en cuenta los siguientes puntos.

1. Entender el problema : Aunque parezca lógico, pero entender el enunciado del problema y comprender lo que se nos pide, es una de las mejores formas de averiguar lo que queremos llegar a obtener mediante el ejercicio, la información que se nos proporciona y que se nos solicita encontrar.
2. Dibuja un diagrama de cuerpo libre: Debemos representar el problema en un diagrama simplificado, mostrando el plano inclinado, el objeto y todas las fuerzas que actúan sobre él. Esto incluye la fuerza de gravedad (peso), la normal, la fuerza de fricción (si existe), y cualquier otra fuerza externa aplicada
3. Descomponer las fuerzas: Este paso es fundamental, lo aplicamos en el método analítico para sumar vectores, y consiste en dividir la fuerza de gravedad (peso) en sus componentes paralelas y perpendiculares al plano inclinado. Si el plano inclinado forma un ángulo con la horizontal, se tendrá que utilizar a la trigonometría para calcular esta componente.
4. Aplica la segunda ley de Newton: Tendremos que utilizar la segunda ley de Newton (F = ma) para resolver el problema. En la dirección paralela al plano inclinado, la suma de las fuerzas es igual a la masa del objeto multiplicada por su aceleración. En la dirección perpendicular al plano inclinado, la suma de las fuerzas es igual a cero si el objeto no se mueve en esa dirección.
5. Considera la fricción: Si hay fuerza de fricción presente, trata de tener en cuenta su dirección y magnitud. La fuerza de fricción puede ser estática o cinética, dependiendo de si el objeto está en reposo o en movimiento.
6. Aplica las leyes de la cinemática: Si el problema involucra el movimiento del objeto a lo largo del plano inclinado, puedes utilizar las ecuaciones de la cinemática para calcular la velocidad, la aceleración, el tiempo o la distancia recorrida.
7. Resuelve el problema: Utiliza las ecuaciones adecuadas para resolver el sistema de ecuaciones y encontrar las incógnitas solicitadas en el problema

Siguiendo estos pasos, podrás resolver un problema de plano inclinado sin dificultad, pero no hay nada mejor que aprender mediante los ejemplos resueltos de plano inclinado que enseñaremos en fisimat, así que comencemos con algunos ejemplos prácticos.

Ejercicios Resueltos de Plano Inclinado

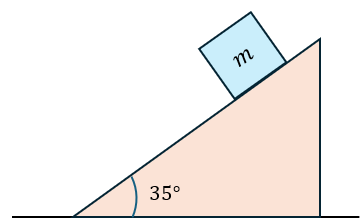
Solución:

a) Para encontrar la aceleración del bloque, primero es necesario hacer un diagrama de fuerzas que permita encontrar la fuerza que provoca que el bloque se deslice por el plano inclinado. Como se observa en la imagen de abajo.

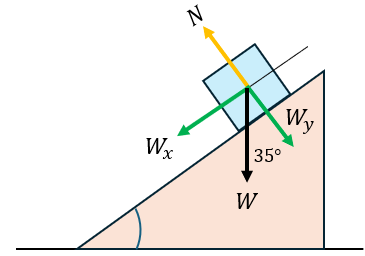
Como se puede ver, la componente horizontal del peso $\displaystyle {{W}_{x}}$  que es paralela al plano inclinado, es la fuerza que provoca que el plano descienda. Esta fuerza se calcula mediante:

$\displaystyle {{W}_{x}}=wsen\alpha =\left( {1.4kg} \right)\left( {9.81} \right)sen\left( {35{}^\circ } \right)=-7.87N$

Se coloca negativo, porque el bloque está deslizando del lado izquierdo

De acuerdo con la segunda ley de Newton, esta fuerza provoca que el bloque acelere hacia abajo; la acleración está dada por:

$\displaystyle a=\frac{F}{m}=\frac{{-7.87N}}{{1.4kg}}=-0.563\frac{m}{{{{s}^{2}}}}$

b) Ya que se conoce la aceleración, es posible encontrar el tiempo que tardó el bloque en descender a lo largo de una distancia d = -1.7 m utilizando la expresión:

$\displaystyle d=\frac{1}{2}a{{t}^{2}}$

Despejando el tiempo se obtiene:

$\displaystyle t=\sqrt{{\frac{{2d}}{a}}}=\sqrt{{\frac{{2\left( {-1.7m} \right)}}{{-5.63\frac{m}{{{{s}^{2}}}}}}}}=0.77s$

c) Si se considera que el bloque parte del reposo, entonces la velocidad con la que éste toca el piso es:

$\displaystyle v=at$

$\displaystyle v=at=-5.63\frac{m}{{{{s}^{2}}}}\cdot 0.77s=-4.34\frac{m}{s}$

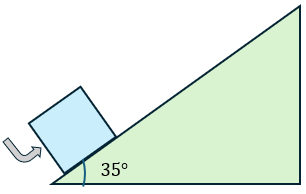
Solución:

a) Para poder encontrar la distancia que recorrerá el bloque, será a través de su aceleración, aunque unicamente obtendremos una aceleración en la componente en "x"

$\displaystyle {{a}_{x}}=gsen\theta =\left( {9.8\frac{m}{{{{s}^{2}}}}} \right)sen\left( {35{}^\circ } \right)=5.62\frac{m}{{{{s}^{2}}}}$

La distancia recorrida es:

$\displaystyle d=\frac{{{{v}_{f}}^{2}-{{v}_{0}}^{2}}}{{2{{a}_{x}}}}=\frac{{0-{{{\left( {3.9\frac{m}{{{{s}^{2}}}}} \right)}}^{2}}}}{{2\left( {5.62\frac{m}{{{{s}^{2}}}}} \right)}}=1.35m$

b) ¿Cuánto tiempo tarda el movimiento de subida del bloque?

Para obtener el tiempo, lo haremos con la siguiente fórmula:

$\displaystyle t=\frac{{{{v}_{f}}-{{v}_{0}}}}{{{{a}_{x}}}}=\frac{{0-3.9\frac{m}{s}}}{{5.63\frac{m}{{{{s}^{2}}}}}}=0.69s$

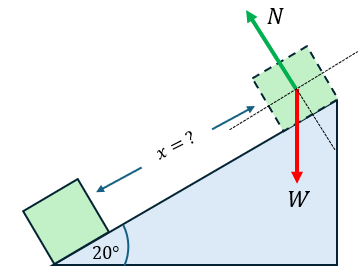
Solución:

Aplicando la segunda ley de Newton, vamos a obtener su aceleración

$\displaystyle \sum{{{{F}_{x}}=ma}}$

$\displaystyle {{W}_{x}}=ma$

Pero en la descomposición rectangular del peso

$\displaystyle {{W}_{x}}=Wsen\left( {20{}^\circ } \right)$

Entonces:

$\displaystyle Wsen\left( {20{}^\circ } \right)=ma$

$\displaystyle mgsen\left( {20{}^\circ } \right)=ma$

$\displaystyle gsen\left( {20{}^\circ } \right)=a$

desepejando a "a"

$\displaystyle a=gsen\left( {20{}^\circ } \right)=3.351\frac{m}{{{{s}^{2}}}}$

Pero como la velocidad inicial es de 5 m/s, aplicamos:

$\displaystyle {{v}_{f}}^{2}={{v}_{0}}^{2}-2ax$

$\displaystyle {{v}_{f}}^{2}=2ax$

despejando a "x"

$\displaystyle x=\frac{{{{v}_{f}}^{2}}}{{2a}}$

$\displaystyle x=\frac{{{{v}_{f}}^{2}}}{{2a}}=\frac{{{{5}^{2}}}}{{2\left( {3.351} \right)}}=\frac{{25}}{{6.703}}=3.729m$

Por lo que la respuesta equivale a 3.729 metros

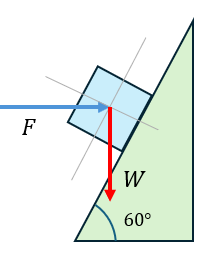
Solución:

a) Obteniendo la magnitud de la fuerza

Analizando nuestro diagrama de cuerpo libre en el plano inclinado, vamos a realizar la suma de fuerzas en el eje x

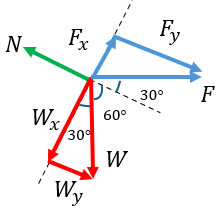
$ \displaystyle \sum{{{{F}_{x}}=0}}$

$\displaystyle {{F}_{x}}-{{W}_{x}}=0$

Descomponiendo en su forma rectangular los vectores de fuerza y peso

$\displaystyle {{F}_{x}}=F\cos (60{}^\circ )$

$\displaystyle {{W}_{x}}=Wsen(60{}^\circ )$

Realizando la sumatoria de fuerzas:

$\displaystyle F\cos (60{}^\circ )=Wsen60{}^\circ $

$ \displaystyle F=\left( {2kg} \right)\left( {9.8\frac{m}{{{{s}^{2}}}}} \right)\frac{{sen60{}^\circ }}{{\cos 60{}^\circ }}=33.94N$

Qué sería el valor de la fuerza.

b) Obteniendo la fuerza normal ejercida por el plano inclinado sobre el bloque

Ahora para encontrar el valor de la fuerza normal ejercida por el plano inclinado sobre el bloque (ignorando la fricción)

$\displaystyle \sum{{{{F}_{y}}}}=0$

$\displaystyle N-{{W}_{y}}-{{F}_{y}}=0$

Primero, vamos a descomponer en su forma rectangular de la fuerza y el peso

$\displaystyle {{W}_{y}}=W\cos \left( {60{}^\circ } \right)$

$\displaystyle {{F}_{y}}=Fsen\left( {60{}^\circ } \right)$

Vamos a reemplazar esto en la ecuación de la fuerza en Y

$\displaystyle N-W\cos \left( {60{}^\circ } \right)-F\cos \left( {60{}^\circ } \right)=0$

$\displaystyle N-mg\cos \left( {60{}^\circ } \right)-\left( {33.94N} \right)\cos \left( {60{}^\circ } \right)=0$

$\displaystyle N-\left( {2kg} \right)\left( {9.8\frac{m}{{{{s}^{2}}}}} \right)\left( {0.5} \right)-\left( {33.94N} \right)\left( {0.866} \right)=0$

$\displaystyle N-9.8-29.39=0$

$\displaystyle N=39.19N$

Por lo cuál se resolvería este problema

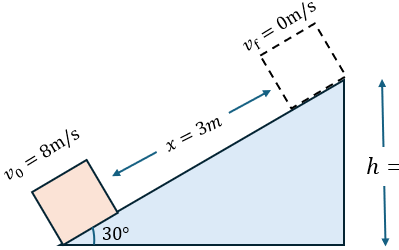
Solución:

a) El cambio en la energía cinética del bloque

Vamos a comenzar calculando la energía cinética del bloque, desde que comienza con los 8 m/s y termina con los 0 m/s.

$\displaystyle {{E}_{{c0}}}=\frac{1}{2}m{{v}_{0}}^{2}=\frac{1}{2}\left( {5kg} \right){{\left( {8\frac{m}{s}} \right)}^{2}}=160J$

Ahora calculamos la energía cinética final

$\displaystyle {{E}_{{cf}}}=\frac{1}{2}m{{v}_{f}}^{2}=\frac{1}{2}\left( {5kg} \right){{\left( {0\frac{m}{s}} \right)}^{2}}=0J$

El cambio de energía cinética, sería:

$\displaystyle \Delta {{E}_{c}}=E{{c}_{f}}-E{{c}_{0}}=0-160J=-160J$

b) El cambio en la energía potencial del bloque

Para poder calcular la energía potencial es necesario conocer la altura del plano inclinado, por ello debemos primero obtener su altura, aplicando un poco de trigonometría, obtenemos:

$\displaystyle sen(30{}^\circ )=\frac{h}{3}$

$\displaystyle h=3sen\left( {30{}^\circ } \right)=1.5m$

Ahora si podemos obtener la energía potencial inicial y final.

$\displaystyle {{E}_{{p0}}}=mgh=\left( {5kg} \right)\left( {9.8\frac{m}{{{{s}^{2}}}}} \right)\left( {0m} \right)=0J$

Obteniendo la energía potencial final

$\displaystyle {{E}_{{pf}}}=mgh=\left( {5kg} \right)\left( {9.8\frac{m}{{{{s}^{2}}}}} \right)\left( {1.5m} \right)=73.5J$

Obteniendo el cambio de energía potencial:

$\displaystyle \Delta {{E}_{p}}=73.5J-0J=73.5J$

c) Obteniendo la aceleración del bloque

Para obtener la aceleración del bloque, al no tener tiempo como dato, vamos a calcularlo mediante la siguiente fórmula:

$\displaystyle {{V}_{f}}^{2}={{V}_{0}}^{2}-2ax$

Despejando y obteniendo a la aceleración:

$\displaystyle a=\frac{{{{v}_{0}}^{2}}}{{2x}}=\frac{{{{{\left( {8\frac{m}{s}} \right)}}^{2}}}}{{2\left( {3m} \right)}}=10.66\frac{m}{{{{s}^{2}}}}$

Nota: la aceleración debería ser $\displaystyle a=-10.66\frac{m}{{{{s}^{2}}}}$ , es negativa porque el movimiento pierde velocidad hasta que sea cero, es decir un tipo de movimiento retardado.

d) Obtener la fuerza de fricción ejercida sobre el bloque

Para obtener la fuerza de fricción ejercida sobre el bloque, será necesario que obtengamos el diagrama de cuerpo libre del problema, agregando todas las fuerzas que participan

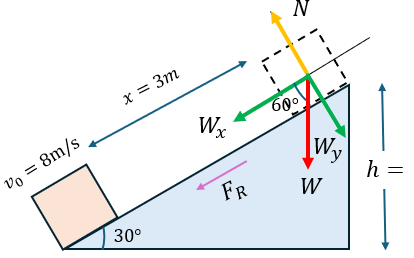
Antes de hacer la sumatoria en "x" y en "y" , vamos a obtener las componentes del peso:

$\displaystyle {{W}_{x}}=wsen30{}^\circ =\left( {5kg} \right)\left( {9.8\frac{m}{{{{s}^{2}}}}} \right)sen(30{}^\circ )=24.5N$

$\displaystyle {{W}_{y}}=w\cos 30{}^\circ =\left( {5kg} \right)\left( {9.8\frac{m}{{{{s}^{2}}}}} \right)\cos (30{}^\circ )=42.43N$

Ahora vamos a obtener las fuerzas que actúan en el eje Y

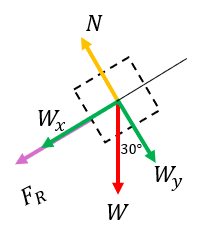
Si observamos solamente tenemos dos fuerzas actuando, la fuerza normal y el peso en y

$\displaystyle \sum{{{{F}_{y}}=N-{{W}_{y}}}}=0$

$\displaystyle N={{W}_{y}}$

O sea que la fuerza normal, será igual al peso en la componente "y"

$\displaystyle N=42.43N$

Recordemos que la fuerza de fricción, tiene por fórmula:

$\displaystyle {{F}_{R}}=\mu N$

Con los datos que tenemos, deducimos entonces que:

$\displaystyle {{F}_{R}}=\left( {42.43} \right)\mu $

Será suficiente, para obtener las fuerzas resultantes en "x" al aplicar la segunda ley de Newton

$\displaystyle \sum{{{{F}_{x}}}}=ma$

$\displaystyle -{{W}_{x}}-{{F}_{R}}=ma$

$\displaystyle -{{W}_{x}}-{{F}_{R}}=ma$

Susituyendo nuestros datos:

$\displaystyle -24.5-42.43\mu =\left( {5kg} \right)\left( {-10.66\frac{m}{{{{s}^{2}}}}} \right)$

Haciendo las operaciones matemáticas, obtenemos que:

$\displaystyle \mu =\frac{{28.8}}{{42.43}}=0.678$

Con esto obtenemos el coeficiente de fricción cinético.

Por lo que la fuerza de fricción es:

$\displaystyle {{F}_{R}}=\mu N$

$\displaystyle {{F}_{R}}=\left( {0.678} \right)\left( {42.43N} \right)=28.8N$

Y problema resuelto 🤓

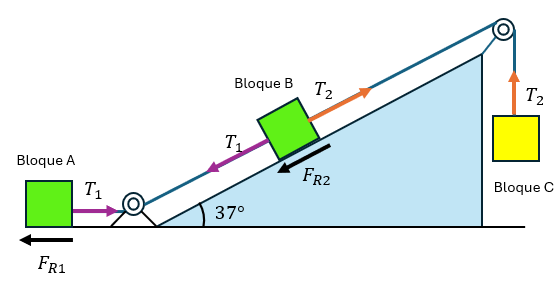
Solución:

a) Calcular la tensión de la cuerda que uno los bloques A y B

Bloque A)

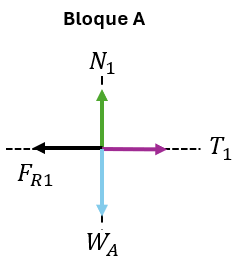
Como el problema indica que el bloque se mueve con velocidad constante, entonces concluimos que la aceleración es cero. Por lo tanto, las sumatoria de fuerzas en x serán de la siguiente manera:

$\displaystyle \sum{{{{F}_{x}}=0}}$

Observando el diagrama para el bloque A, vemos que nuestra ecuación queda expresada de la siguiente manera:

$\displaystyle {{T}_{1}}-{{F}_{{R1}}}=0$

$\displaystyle {{T}_{1}}={{F}_{{R1}}}$

Ahora obtenemos la sumatoria de fuerzas en el eje y

$\displaystyle \sum{{{{F}_{y}}=0}}$

$\displaystyle {{W}_{A}}-{{N}_{1}}=0$

$\displaystyle {{W}_{A}}={{N}_{1}}=20N$

Con este dato de la fuerza normal, podemos obtener la fricción en ese bloque y su tensión

$\displaystyle {{F}_{{R1}}}=\mu {{N}_{1}}=\left( {0.5} \right)\left( {20N} \right)=10N$

Entonces

$\displaystyle {{T}_{1}}={{F}_{{R1}}}=10N$

Bloque B)

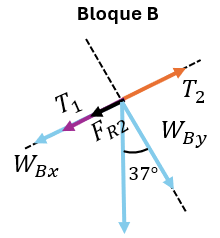
Debido a que se desplaza el bloque a velocidad constante hacia la derecha, luego la aceleración es cero.

$\displaystyle \sum{{{{F}_{x}}}}=0$

$\displaystyle {{T}_{2}}-{{W}_{{Bx}}}-{{T}_{1}}-{{F}_{{R2}}}=0$ (Ecuación 1)

La componente del peso en y del bloque B

$\displaystyle {{W}_{{Bx}}}={{W}_{B}}sen\left( {37{}^\circ } \right)$

$\displaystyle {{W}_{{Bx}}}=20sen\left( {37{}^\circ } \right)=12.036N$

Como ya sabemos que: $\displaystyle {{T}_{1}}=10N$

Aplicando la sumatoria de fuerzas en "y" en el bloque B

$\displaystyle \sum{{{{F}_{y}}=0}}$

$\displaystyle {{W}_{{By}}}-{{N}_{2}}=0$

$\displaystyle {{W}_{{By}}}={{N}_{2}}={{W}_{B}}\cos \left( {37{}^\circ } \right)=20\cos 37{}^\circ $

$\displaystyle {{W}_{{By}}}={{N}_{2}}=15.972N$

Obteniendo la fuerza de fricción

$\displaystyle {{F}_{{R2}}}=\mu {{N}_{2}}=\left( {0.5} \right)\left( {15972} \right)=7.986N$

Reemplazando en la (Ecuación 1), para encontrar la $\displaystyle {{T}_{2}}$

$\displaystyle {{T}_{2}}-{{W}_{{Bx}}}-{{T}_{1}}-{{F}_{{R2}}}=0$

$\displaystyle {{T}_{2}}={{W}_{{Bx}}}+{{T}_{1}}+{{F}_{{R2}}}$

$\displaystyle {{T}_{2}}=12.036+10+7.986=30N$

C) Analizando el peso del bloque C

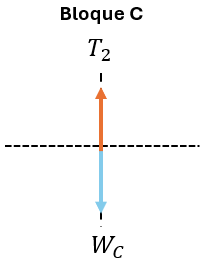
Analizando el Bloque C)

Porque se desplaza a velocidad constante hacia la derecha, luego la aceleración es cero.

$\displaystyle \sum{{{{F}_{y}}=0}}$

$\displaystyle {{W}_{c}}-{{T}_{2}}=0$

$\displaystyle {{W}_{c}}={{T}_{2}}=30N$