Energía Potencial Gravitacional - Ejercicios Resueltos

La energía potencial gravitacional o energía potencial gravitatoria es un tipo de energía muy importante en Física, pues se manifiesta simplemente al levantar cualquier cuerpo a una cierta altura. Esto también ocasiona que la persona realice un trabajo , porque implica la fuerza con que levanta al objeto y la altura a donde la logra levantar, a esto es lo que llamamos energía potencial gravitatoria o gravitacional.

Peros si observamos cuidadosamente el término "gravitatorio" o "gravitacional" vemos que implica el nombre de gravedad , esto es porque el origen de la energía potencial es debido a la atracción gravitacional de la tierra sobre el cuerpo.

📏 Fórmula de la Energía Potencial Gravitacional

La fórmula de la energía potencial gravitacional es muy fácil de aprender y de identificar, pues matemáticamente se expresa de la siguiente manera:

Donde:

Ep = Energía potencial gravitacional (medida en Joules) -> J

m  = masa del cuerpo u objeto (medida en Kg )

g = gravedad o valor de la constante gravitatoria (g) = 9.8 m/s²

h = altura a la que está elevada el cuerpo u objeto (medida en metros) -> m

🤔 ¿Cómo funciona la energía potencial gravitacional?

Veamos la siguiente imagen:

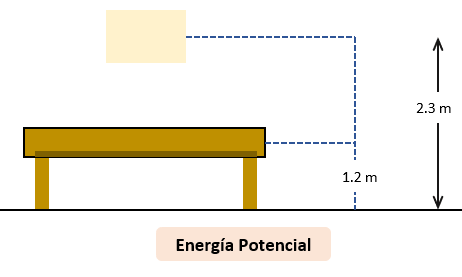
La energía potencial gravitacional de cualquier cuerpo localizado a cierta altura, depende del nivel tomado como referencia para obtener el cálculo de su energía.

Caso 1: Supongamos que el bloque tiene una masa de 3kg y deseamos encontrar la energía potencial respecto a la mesa. Entonces podríamos decir que la altura que necesitamos conocer para este cálculo tiene que partir de la diferencia entre la altura total de 2.3m respecto al suelo, y de 1.2m también respecto al suelo pero de la mesa. Entonces:

$latex \displaystyle {{h}_{bloque-mesa}}=2.3m-1.2m=1.1m$

Ahora si podemos realizar nuestro cálculo de energía potencial para el bloque respecto a la mesa. Aplicamos la fórmula:

$latex \displaystyle {{E}_{p}}=mgh=\left( 3kg \right)\left( 9.8\frac{m}{{{s}^{2}}} \right)\left( 1.1m \right)=32.34J$

Lo que significa que la energía potencial es de 32.34 Joules.

Veamos el otro caso.

Caso 2: Supongamos que ahora deseamos encontrar la energía potencial del bloque pero respecto al suelo, entonces nuestro cálculo sería diferente, pues la distancia hacía al suelo es de 2.3 metros, ahora solamente sustituimos en la fórmula:

$latex \displaystyle {{E}_{p}}=mgh=\left( 3kg \right)\left( 9.8\frac{m}{{{s}^{2}}} \right)\left( 2.3m \right)=67.62J$

Uff 😀

Lo que esperábamos un aumento en la energía potencial debido a que hay más altura, entonces concluimos lo siguiente.

📄 Ejercicios Resueltos de Energía Potencial Gravitacional

Veamos algunos ejemplos y problemas resueltos de energía potencial gravitacional. Desde lo más básico a problemas un poco más complejos.

Solución: 

Podríamos omitir una imagen del problema, porque tenemos los datos necesarios para sustituir en la fórmula, sin embargo muchas veces es importante contar con una imagen para las personas que todavía no comprenden el concepto.  Veamos!

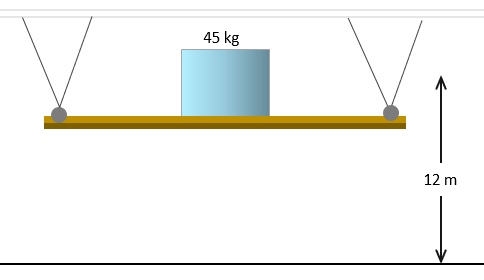
Recopilando nuestros datos:

Datos:

Ep = ?

m = 45 kg

g = 9.8 m/s²

h = 12 m

Para obtener la energía potencial de dicho caja de acero, bastará con sustituir los datos que tenemos a la vista, y multiplicar.

$latex \displaystyle {{E}_{p}}=mgh=\left( 45kg \right)\left( 9.8\frac{m}{{{s}^{2}}} \right)\left( 12m \right)=5292J$

Esto es una energía potencial de 5292 Joules.

Solución:

Para este problema, tenemos que analizar nuestros datos:

Datos:

Ep = 450 J

m = 35 kg

g = 9.8 m/s²

h = ?

Como es la altura, la que debemos encontrar, entonces vamos a despejar a "h" de nuestra fórmula.

$latex \displaystyle {{E}_{p}}=mgh$

Despejando "h"

$latex \displaystyle h=\frac{{{E}_{p}}}{mg}$

Si no sabes despejar, puedes ver varios ejemplos aquí.

Sustituyendo nuestros datos en la fórmula:

$latex \displaystyle h=\frac{{{E}_{p}}}{mg}=\frac{450J}{\left( 35kg \right)\left( 9.8\frac{m}{{{s}^{2}}} \right)}=1.31m$

Para que el niño pueda tener una energía potencial de 450 Joules, solo necesita estar a una altura de 1.31 metros. 😀

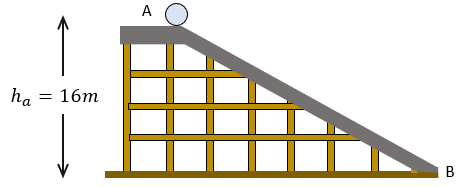
Solución:

Para ambos casos analizaremos lo siguiente:

En el Punto A:

Datos:

Ep = ?

m = 2.5 kg

h = 16 m

g = 9.8 m/s²

Sustituyendo en nuestra fórmula:

$latex \displaystyle {{E}_{p}}=mgh=\left( 2.5kg \right)\left( 9.8\frac{m}{{{s}^{2}}} \right)\left( 16m \right)=392J$

Es la energía potencial que tiene nuestra pelota a esa altura.

En el punto B:

Datos:

Ep = ?

m = 2.5 kg

h = 0 m

g = 9.8 m/s²

Sustituyendo en nuestra fórmula:

$latex \displaystyle {{E}_{p}}=mgh=\left( 2.5kg \right)\left( 9.8\frac{m}{{{s}^{2}}} \right)\left( 0m \right)=0J$

Como podemos observar, la energía potencial en el punto B es nula, es decir no hay. Esto es porque la energía potencial se acaba de convertir en energía cinética.