Módulo de Young - Ejercicios Resueltos
¡Qué tal amigos de Fisimat, dando seguimiento a nuestra serie sobre elasticidad, y después de haber introducido los conceptos de esfuerzo, deformación unitaria y la Ley de Hooke, ha llegado el momento de profundizar en una de las propiedades más importantes que caracterizan la respuesta mecánica de los materiales: el Módulo de Young. Este módulo, también conocido como Módulo de Elasticidad Longitudinal, es fundamental para cuantificar la rigidez de un material y predecir cómo se deformará bajo cargas axiales. 😵
Introducción
El Módulo de Young ($E$) es una constante que describe la rigidez de un material elástico sólido cuando se somete a fuerzas de tracción o compresión en la dirección de su longitud. Nombrado en honor al científico británico Thomas Young, este módulo relaciona directamente el esfuerzo normal aplicado con la deformación unitaria longitudinal que experimenta el material, siempre y cuando este se encuentre dentro de su límite elástico, donde la deformación es reversible y proporcional al esfuerzo.

[alert-warning] Comprender el Módulo de Young es esencial en una vasta gama de aplicaciones científicas y de ingeniería. Permite a los ingenieros seleccionar los materiales adecuados para cada aplicación, asegurando que las estructuras y componentes puedan soportar las cargas previstas sin deformarse excesivamente o fallar. Desde el diseño de cables y vigas en la construcción civil hasta la fabricación de componentes precisos en la industria aeroespacial o la creación de implantes biocompatibles en medicina, el Módulo de Young es un parámetro de diseño crítico. Este artículo explorará en detalle su definición, cómo se determina, sus valores para diversos materiales y su importancia práctica. [/alert-warning]
Definición del Módulo de Young ($E$)
Para definir el Módulo de Young, primero debemos recordar brevemente los conceptos de esfuerzo normal y deformación unitaria longitudinal.
Recordando Esfuerzo Normal y Deformación Unitaria Longitudinal
El esfuerzo normal ($\sigma$) se define como la fuerza ($F$) aplicada perpendicularmente a un área de sección transversal ($A$):
$$\sigma = \frac{F}{A}$$
La deformación unitaria longitudinal ($\epsilon$) es el cambio en la longitud ($\Delta L$) por unidad de longitud original ($L_0$):
$$\epsilon = \frac{\Delta L}{L_0}$$
Ambos conceptos fueron introducidos en nuestro primer artículo de la serie y si tienes dudas, te recordamos con esta imagen.
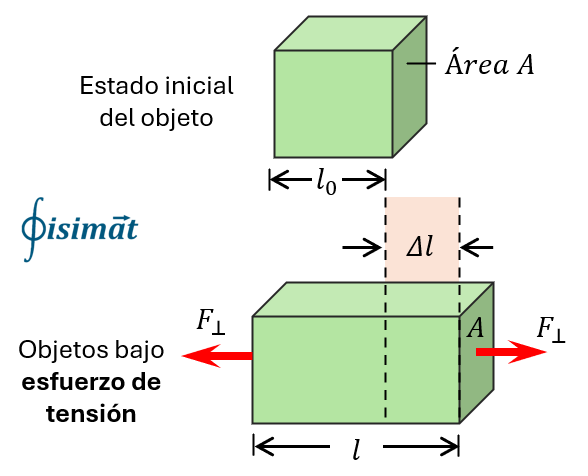
El Módulo de Young como Constante de Proporcionalidad
Como vimos en el artículo sobre la Ley de Hooke, para muchos materiales en su región elástica, el esfuerzo es directamente proporcional a la deformación unitaria. Para el caso de esfuerzos y deformaciones normales (tracción o compresión), esta relación se expresa como:
$$\sigma = E\epsilon$$
El Módulo de Young ($E$) es precisamente esta constante de proporcionalidad. Por lo tanto, se define como la relación entre el esfuerzo normal y la deformación unitaria longitudinal:
$$E = \frac{\text{Esfuerzo Normal}}{\text{Deformación Unitaria Longitudinal}} = \frac{\sigma}{\epsilon}$$
Las unidades del Módulo de Young en el Sistema Internacional son las mismas que las del esfuerzo: Pascales (Pa) o Newtons por metro cuadrado ($N/m^2$). Debido a los grandes valores que suele tomar para la mayoría de los materiales estructurales, es común expresarlo en Megapascales (MPa, $10^6 \text{ Pa}$) o Gigapascales (GPa, $10^9 \text{ Pa}$).
[alert-note]
Ejemplo: Si un material tiene un Módulo de Young de $E = 200 \text{ GPa}$ y se le aplica un esfuerzo normal de $\sigma = 100 \text{ MPa}$, ¿cuál será la deformación unitaria resultante?
[/alert-note]
Solución:
Primero, aseguramos unidades consistentes:
$\sigma = 100 \text{ MPa} = 100 \times 10^6 \text{ Pa}$. $E = 200 \text{ GPa} = 200 \times 10^9 \text{ Pa}$.
De la fórmula $E = \frac{\sigma}{\epsilon}$, despejamos $\epsilon$:
$\epsilon = \frac{\sigma}{E} = \frac{100 \times 10^6 \text{ Pa}}{200 \times 10^9 \text{ Pa}} = \frac{100}{200000} = 0.0005$.
La deformación unitaria resultante es $0.0005$ (o $500 \mu\epsilon$).
Significado Físico del Módulo de Young
El Módulo de Young es una medida intrínseca de la rigidez de un material sólido frente a la deformación elástica bajo cargas axiales.
- Un valor alto de $E$ indica que el material es muy rígido; es decir, se necesita una gran cantidad de esfuerzo para producir una pequeña deformación. Ejemplos: acero, tungsteno, cerámicas.
- Un valor bajo de $E$ indica que el material es flexible; es decir, se deforma considerablemente bajo esfuerzos relativamente pequeños. Ejemplos: caucho, polietileno, tejidos blandos.
Es importante distinguir entre rigidez (descrita por el Módulo de Young) y resistencia (que se refiere al esfuerzo máximo que un material puede soportar antes de fracturarse o fluir plásticamente). Un material puede ser muy rígido pero no necesariamente muy resistente, y viceversa. El Módulo de Young se refiere específicamente al comportamiento en la región elástica.
Determinación Experimental y Valores Típicos
El Módulo de Young es una propiedad del material que se determina experimentalmente. 🧪
Ensayo de Tracción y la Curva Esfuerzo-Deformación
El método más común para determinar el Módulo de Young es mediante un ensayo de tracción. En este ensayo, una muestra del material de dimensiones estandarizadas (probeta) se somete a una fuerza de tracción gradualmente creciente mientras se miden simultáneamente la fuerza aplicada y el alargamiento de la probeta.

A partir de los datos de fuerza y alargamiento, se pueden calcular los valores de esfuerzo ($\sigma$) y deformación unitaria ($\epsilon$) correspondientes. Al graficar $\sigma$ en función de $\epsilon$, se obtiene la curva esfuerzo-deformación característica del material. El Módulo de Young ($E$) se determina como la pendiente de la porción lineal inicial de esta curva, que corresponde a la región elástica donde se cumple la Ley de Hooke.
$$E = \frac{\Delta\sigma}{\Delta\epsilon} \text{ (en la región lineal elástica)}$$
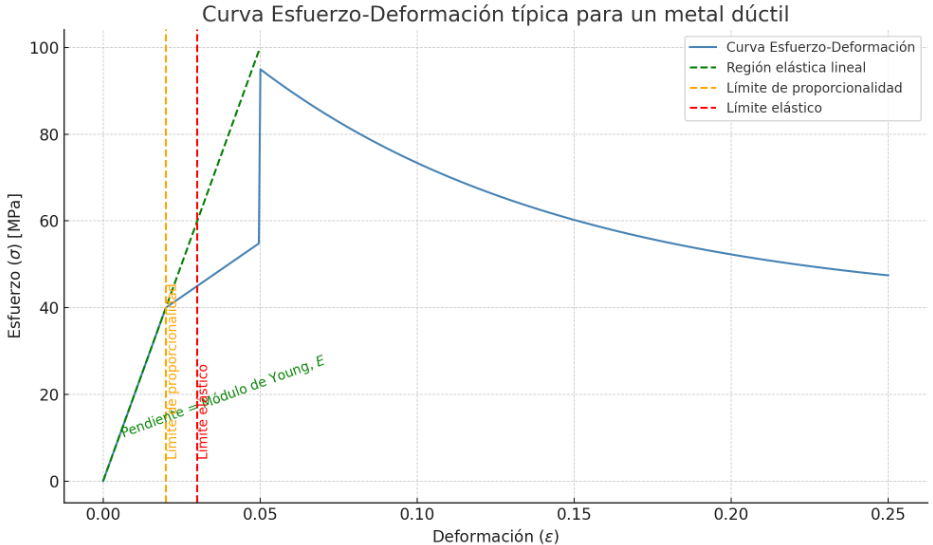
Valores del Módulo de Young para Diversos Materiales
El Módulo de Young es una propiedad intrínseca, lo que significa que es característico de cada material, aunque puede variar ligeramente dependiendo de la composición exacta, el tratamiento térmico, la microestructura y la temperatura. A continuación, se presentan algunos valores típicos aproximados del Módulo de Young para materiales comunes a temperatura ambiente:
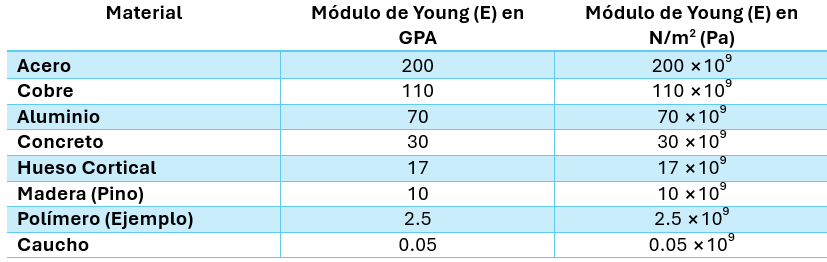
[alert-note] Ejemplo Comparar la rigidez del acero ($E \approx 200 \text{ GPa}$) con la del aluminio ($E \approx 70 \text{ GPa}$). Si se aplica el mismo esfuerzo normal a dos barras idénticas en dimensiones, una de acero y otra de aluminio, ¿cuál se deformará más? [/alert-note]
Solución:
Dado que $E = \sigma/\epsilon$, entonces $\epsilon = \sigma/E$. Para el mismo esfuerzo $\sigma$:
$\epsilon_{acero} = \sigma / (200 \text{ GPa})$
$\epsilon_{aluminio} = \sigma / (70 \text{ GPa})$
Como $70 \text{ GPa} < 200 \text{ GPa}$, la deformación unitaria del aluminio será mayor que la del acero. Por lo tanto, la barra de aluminio se deformará más.
Aplicaciones del Módulo de Young
El conocimiento del Módulo de Young es vital en muchas áreas de la ingeniería y el diseño.
Selección de Materiales en Diseño e Ingeniería
Los ingenieros utilizan el Módulo de Young para seleccionar materiales que cumplan con los requisitos de rigidez de una aplicación específica. Por ejemplo, para una viga que no debe flexionarse mucho bajo carga, se preferirá un material con un alto $E$. Para componentes que necesitan ser flexibles, se elegirán materiales con un $E$ bajo.
Cálculo de Deformaciones Elásticas
Una de las aplicaciones más directas es el cálculo de la deformación (alargamiento o acortamiento) de un miembro estructural bajo una carga axial. Combinando las definiciones de esfuerzo, deformación y Módulo de Young:
$\sigma = F/A$, $\epsilon = \Delta L/L_0$, y $\sigma = E\epsilon$.
Sustituyendo, obtenemos $F/A = E (\Delta L/L_0)$. Despejando $\Delta L$:
$$\Delta L = \frac{FL_0}{AE}$$
Esta fórmula es ampliamente utilizada para predecir deformaciones elásticas.
[alert-note] Ejemplo Una barra de aluminio ($E = 70 \text{ GPa}$) de $2 \text{ m}$ de longitud y $1 \text{ cm}^2$ ($1 \times 10^{-4} \text{ m}^2$) de área de sección transversal se somete a una carga de tracción de $14 \text{ kN}$ ($14000 \text{ N}$). ¿Cuánto se alarga la barra?[/alert-note]
Solución:
$E = 70 \text{ GPa} = 70 \times 10^9 \text{ N/m}^2$.
$\Delta L = \frac{(14000 \text{ N})(2 \text{ m})}{(1 \times 10^{-4} \text{ m}^2)(70 \times 10^9 \text{ N/m}^2)} = \frac{28000}{7 \times 10^6} \text{ m} = \frac{28}{7} \times 10^{-3} \text{ m} = 4 \times 10^{-3} \text{ m} = 4 \text{ mm}$.
La barra se alarga $4 \text{ mm}$.
Importancia en el Análisis Estructural
En el análisis de estructuras complejas, como puentes, edificios o armaduras, el Módulo de Young de los materiales componentes es un dato crucial para los modelos computacionales (ej. Método de Elementos Finitos) que predicen cómo se distribuirán los esfuerzos y cómo se deformará la estructura bajo diversas condiciones de carga, garantizando su estabilidad y seguridad.
Factores que Pueden Afectar el Módulo de Young
Si bien el Módulo de Young se considera una propiedad del material, algunos factores pueden influir en su valor:
- Temperatura: En general, para la mayoría de los metales y muchos otros materiales, el Módulo de Young tiende a disminuir a medida que aumenta la temperatura.
- Composición y Microestructura: Pequeñas variaciones en la aleación, el tamaño de grano, la presencia de impurezas o defectos (como porosidad) pueden afectar el valor de $E$.
- Tratamientos Térmicos o Mecánicos: Procesos como el templado, el recocido o el trabajo en frío pueden alterar la microestructura y, en consecuencia, el Módulo de Young.
- Anisotropía: Algunos materiales (como la madera o los compuestos reforzados con fibra) son anisotrópicos, lo que significa que su Módulo de Young varía según la dirección en la que se aplica la fuerza con respecto a la estructura interna del material.
Para la mayoría de los cálculos introductorios, se utilizan valores promedio o nominales a temperatura ambiente.
Ejercicios Resueltos del Módulo de Young
Solución
▷ Paso 1 Convertir todas las unidades al Sistema Internacional (SI).
$L_0 = 1 \text{ m}$.
$A = 4 \text{ cm}^2 = 4 \times (10^{-2} \text{ m})^2 = 4 \times 10^{-4} \text{ m}^2$.
$\Delta L = 0.5 \text{ mm} = 0.5 \times 10^{-3} \text{ m}$.
$F = 20 \text{ kN} = 20 \times 10^3 \text{ N}$.
▷ Paso 2 Calcular el esfuerzo normal ($\sigma$).
$\sigma = \frac{F}{A} = \frac{20 \times 10^3 \text{ N}}{4 \times 10^{-4} \text{ m}^2} = 5 \times 10^7 \text{ Pa} = 50 \text{ MPa}$.
▷ Paso 3 Calcular la deformación unitaria longitudinal ($\epsilon$).
$\epsilon = \frac{\Delta L}{L_0} = \frac{0.5 \times 10^{-3} \text{ m}}{1 \text{ m}} = 0.5 \times 10^{-3} = 0.0005$.
▷ Paso 4 Calcular el Módulo de Young ($E$).
$E = \frac{\sigma}{\epsilon} = \frac{5 \times 10^7 \text{ Pa}}{0.5 \times 10^{-3}} = \frac{5}{0.5} \times 10^{10} \text{ Pa} = 10 \times 10^{10} \text{ Pa} = 100 \times 10^9 \text{ Pa}$.
▷ Paso 5 Expresar el resultado en Gigapascales (GPa).
$E = 100 \text{ GPa}$.
Respuesta: El Módulo de Young del material es $100 \text{ GPa}$.
Solución
▷ Paso 1 Identificar los datos.
$\epsilon = 0.0008$.
$E = 200 \text{ GPa} = 200 \times 10^9 \text{ Pa}$.
▷ Paso 2 Aplicar la fórmula $\sigma = E\epsilon$.
$\sigma = (200 \times 10^9 \text{ Pa}) \times (0.0008)$.
$\sigma = (200 \times 10^9) \times (8 \times 10^{-4}) \text{ Pa}$.
$\sigma = 1600 \times 10^5 \text{ Pa} = 160 \times 10^6 \text{ Pa}$.
▷ Paso 3 Expresar el resultado en Megapascales (MPa).
$\sigma = 160 \text{ MPa}$.
Respuesta: Se requiere un esfuerzo de $160 \text{ MPa}$.
Solución
▷ Paso 1 Convertir unidades y calcular el área de la sección transversal.
$L_0 = 5 \text{ m}$.
Diámetro $d = 2 \text{ mm} = 0.002 \text{ m}$. Radio $r = 0.001 \text{ m}$.
Área $A = \pi r^2 = \pi (0.001 \text{ m})^2 = \pi \times 10^{-6} \text{ m}^2 \approx 3.14159 \times 10^{-6} \text{ m}^2$.
$F = 300 \text{ N}$.
$E = 110 \text{ GPa} = 110 \times 10^9 \text{ Pa}$.
▷ Paso 2 Usar la fórmula $\Delta L = \frac{FL_0}{AE}$.
$\Delta L = \frac{(300 \text{ N})(5 \text{ m})}{(3.14159 \times 10^{-6} \text{ m}^2)(110 \times 10^9 \text{ Pa})}$.
$\Delta L = \frac{1500}{3.14159 \times 110 \times 10^3} \text{ m}$.
$\Delta L = \frac{1500}{345574.9} \text{ m} \approx 0.004340 \text{ m}$.
▷ Paso 3 Expresar el resultado en milímetros.
$\Delta L \approx 4.34 \text{ mm}$.
Respuesta: El alargamiento del alambre es aproximadamente $4.34 \text{ mm}$.
Solución
▷ Paso 1 Identificar datos y convertir unidades.
$L_0 = 2.5 \text{ m}$.
$\Delta L_{max} = 1.0 \text{ mm} = 1.0 \times 10^{-3} \text{ m}$.
$F = 15 \text{ kN} = 15 \times 10^3 \text{ N}$.
$E = 70 \text{ GPa} = 70 \times 10^9 \text{ Pa}$.
▷ Paso 2 Usar la fórmula $\Delta L = \frac{FL_0}{AE}$ para despejar el Área ($A$).
$A = \frac{FL_0}{E \Delta L_{max}}$.
▷ Paso 3 Calcular el área mínima requerida.
$A = \frac{(15 \times 10^3 \text{ N})(2.5 \text{ m})}{(70 \times 10^9 \text{ Pa})(1.0 \times 10^{-3} \text{ m})} = \frac{37.5 \times 10^3}{70 \times 10^6} \text{ m}^2$.
$A = \frac{37.5}{70000} \text{ m}^2 \approx 0.0005357 \text{ m}^2 = 5.357 \times 10^{-4} \text{ m}^2$.
▷ Paso 4 Calcular el radio ($r$) a partir del área ($A = \pi r^2$).
$r^2 = \frac{A}{\pi} = \frac{5.357 \times 10^{-4} \text{ m}^2}{\pi} \approx 1.705 \times 10^{-4} \text{ m}^2$.
$r \approx \sqrt{1.705 \times 10^{-4}} \text{ m} \approx 0.01306 \text{ m}$.
▷ Paso 5 Calcular el diámetro mínimo ($d = 2r$).
$d = 2 \times 0.01306 \text{ m} \approx 0.02612 \text{ m}$.
▷ Paso 6 Expresar el resultado en milímetros.
$d \approx 26.12 \text{ mm}$.
Respuesta: El diámetro mínimo requerido para la barra es aproximadamente $26.12 \text{ mm}$.
Solución
▷ Paso 1 Relacionar deformación unitaria, esfuerzo y Módulo de Young.
$\epsilon = \frac{\sigma}{E}$. Como las varillas son idénticas y se les aplica la misma fuerza, el esfuerzo $\sigma = F/A$ será el mismo para ambas.
▷ Paso 2 Comparar las deformaciones unitarias.
$\epsilon_A = \frac{\sigma}{E_A}$
$\epsilon_B = \frac{\sigma}{E_B}$
▷ Paso 3 Determinar cuál es mayor.
Como $E_B < E_A$ (25 GPa < 100 GPa), y $\epsilon$ es inversamente proporcional a $E$ para un $\sigma$ constante, entonces $\epsilon_B > \epsilon_A$. La varilla del material B experimentará una mayor deformación unitaria.
▷ Paso 4 Calcular la proporción $\epsilon_B / \epsilon_A$.
$\frac{\epsilon_B}{\epsilon_A} = \frac{(\sigma/E_B)}{(\sigma/E_A)} = \frac{\sigma}{E_B} \times \frac{E_A}{\sigma} = \frac{E_A}{E_B}$.
$\frac{\epsilon_B}{\epsilon_A} = \frac{100 \text{ GPa}}{25 \text{ GPa}} = 4$.
Respuesta: La varilla del material B (el menos rígido) experimentará una mayor deformación unitaria. La deformación unitaria de la varilla B será 4 veces mayor que la de la varilla A.
Solución
▷ Paso 1 Identificar datos y convertir unidades si es necesario.
$L_0 = 50 \text{ mm}$.
$L_f = 50.075 \text{ mm}$.
$\sigma = 140 \text{ MPa} = 140 \times 10^6 \text{ Pa}$.
▷ Paso 2 Calcular el cambio en longitud ($\Delta L$).
$\Delta L = L_f - L_0 = 50.075 \text{ mm} - 50 \text{ mm} = 0.075 \text{ mm}$.
▷ Paso 3 Calcular la deformación unitaria longitudinal ($\epsilon$).
$\epsilon = \frac{\Delta L}{L_0} = \frac{0.075 \text{ mm}}{50 \text{ mm}} = 0.0015$.
▷ Paso 4 Calcular el Módulo de Young ($E = \sigma/\epsilon$).
$E = \frac{140 \times 10^6 \text{ Pa}}{0.0015} = \frac{140 \times 10^6}{1.5 \times 10^{-3}} \text{ Pa}$.
$E = \frac{140}{1.5} \times 10^9 \text{ Pa} \approx 93.33 \times 10^9 \text{ Pa}$.
▷ Paso 5 Expresar en GPa.
$E \approx 93.33 \text{ GPa}$.
Respuesta: El Módulo de Young del metal es aproximadamente $93.33 \text{ GPa}$.
Solución
▷ Paso 1 Identificar datos y convertir unidades.
$E = 30 \text{ GPa} = 30 \times 10^9 \text{ Pa}$.
$L_0 = 3 \text{ m}$.
$A = 0.1 \text{ m}^2$.
$\Delta L = -0.5 \text{ mm} = -0.5 \times 10^{-3} \text{ m}$ (negativo por acortamiento).
▷ Paso 2 Calcular la deformación unitaria ($\epsilon$).
$\epsilon = \frac{\Delta L}{L_0} = \frac{-0.5 \times 10^{-3} \text{ m}}{3 \text{ m}} \approx -0.00016667$.
(El signo negativo solo indica compresión, para el cálculo del esfuerzo podemos usar el valor absoluto y luego inferir la fuerza de compresión).
▷ Paso 3 Calcular el esfuerzo normal ($\sigma = E\epsilon$).
$\sigma = (30 \times 10^9 \text{ Pa}) \times (0.00016667) \approx 5 \times 10^6 \text{ Pa} = 5 \text{ MPa}$.
▷ Paso 4 Calcular la fuerza ($F = \sigma A$).
$F = (5 \times 10^6 \text{ N/m}^2) \times (0.1 \text{ m}^2) = 0.5 \times 10^6 \text{ N}$.
▷ Paso 5 Expresar en kN.
$F = 500 \times 10^3 \text{ N} = 500 \text{ kN}$.
Respuesta: La magnitud de la carga de compresión es $500 \text{ kN}$.
a) ¿Cuál es el Módulo de Young del polímero?
b) Si una muestra de este polímero con una sección transversal de $50 \text{ mm}^2$ se somete a una fuerza de tracción de $250 \text{ N}$ (asumiendo que sigue en la región elástica), ¿cuál será la deformación unitaria?
Solución
▷ Paso 1 (a) Interpretar la pendiente de la curva esfuerzo-deformación.
La pendiente de la región elástica lineal de la curva $\sigma$-$\epsilon$ es, por definición, el Módulo de Young ($E$).
Por lo tanto, $E = 2.5 \text{ GPa}$.
▷ Paso 2 (b) Calcular el esfuerzo ($\sigma$) para la carga dada.
Área $A = 50 \text{ mm}^2 = 50 \times (10^{-3} \text{ m})^2 = 50 \times 10^{-6} \text{ m}^2 = 5 \times 10^{-5} \text{ m}^2$.
Fuerza $F = 250 \text{ N}$.
$\sigma = \frac{F}{A} = \frac{250 \text{ N}}{5 \times 10^{-5} \text{ m}^2} = 50 \times 10^5 \text{ Pa} = 5 \times 10^6 \text{ Pa} = 5 \text{ MPa}$.
▷ Paso 3 (b) Calcular la deformación unitaria ($\epsilon = \sigma/E$).
$E = 2.5 \text{ GPa} = 2.5 \times 10^9 \text{ Pa}$.
$\sigma = 5 \times 10^6 \text{ Pa}$.
$\epsilon = \frac{5 \times 10^6 \text{ Pa}}{2.5 \times 10^9 \text{ Pa}} = \frac{5}{2500} = \frac{1}{500} = 0.002$.
Respuesta:
a) El Módulo de Young del polímero es $2.5 \text{ GPa}$.
b) La deformación unitaria será $0.002$.
Conclusión
El Módulo de Young ($E$) se erige como una propiedad mecánica fundamental que cuantifica la rigidez de un material, es decir, su resistencia a la deformación elástica cuando se somete a esfuerzos de tracción o compresión. Es la constante de proporcionalidad que vincula el esfuerzo normal con la deformación unitaria longitudinal, tal como lo establece la Ley de Hooke generalizada para materiales. Su determinación a través de ensayos de tracción y el conocimiento de sus valores típicos para diferentes materiales son cruciales para la ingeniería.
La capacidad de calcular el Módulo de Young y utilizarlo para predecir cómo se alargarán o acortarán los componentes bajo carga es indispensable para el diseño seguro y eficiente de prácticamente cualquier estructura o dispositivo. En los siguientes artículos de esta serie sobre elasticidad, exploraremos otros módulos importantes, como el Módulo de Corte y el Módulo Volumétrico, que describen la respuesta de los materiales a otros tipos de esfuerzo, completando así nuestro entendimiento del comportamiento elástico.
¿Te gustó este contenido?
Únete a nuestra comunidad en WhatsApp o Telegram para recibir nuevos proyectos, tutoriales y noticias exclusivas.
Deja una respuesta

Estos temas te pueden interesar