Integrales por Partes - Ejercicios Resueltos
Aprende a como resolver integrales por partes paso a paso 🤓
En nuestros artículos y ejercicios resueltos sobre Cálculo Integral , existe uno de los temas más importantes y que más cuesta a muchos estudiantes de preparatoria y universidad, se trata sobre la Integración por partes , o bien las Integrales por partes. Este tipo de integración puede parecer compleja, pero no lo es, si entendemos realmente el proceso y la lógica. Nos daremos cuenta que no es nada del otro mundo.
Hace algunos meses publicábamos sobre las integrales por sustitución o cambio de variable , recordemos que la mayor parte de las integrales tienen aplicaciones importantes en la ingeniería, y muchos campos de la ciencia, es por ello que debemos tener cuidado al momento de realizar cada integral y no equivocarnos en el proceso. El método por partes se aplica para un producto entre dos funciones, es ahí donde radica la fórmula e integración por éste método. 😀
¿Cómo se obtiene la integral por partes?
Veamos como se obtiene:
Supongamos que tenemos la función de un producto, a dicha función la llamaremos "y". Por lo tanto las dos funciones las pondremos de esta forma, a una como "u" y a otra como "v". Es decir:
$\displaystyle y=uv$
Si derivamos respecto a "x", obtenemos lo siguiente:
$\displaystyle \frac{dy}{dx}=\frac{d}{dx}\left( uv \right)$
¡Atención aquí! , esto se trata de la derivada de un producto
$\displaystyle \frac{dy}{dx}=u\frac{dv}{dx}+v\frac{du}{dx}$
Vamos a multiplicar toda la igualdad por "dx" para eliminar a los denominadores
$\displaystyle dx\left( \frac{dy}{dx}=u\frac{dv}{dx}+v\frac{du}{dx} \right)$
Esto nos da:
$\displaystyle dy=udv+vdu$
Integrando ambos miembros de la igualdad, tenemos:
$\displaystyle \int{dy}=\int{udv}+\int{vdu}$
De las tres integrales, solamente podemos integrar la primera (la del miembro izquierdo), porque es la única que podemos definir su valor, y esto nos da:
$\displaystyle y=\int{udv}+\int{vdu}$
Recordemos que al principio dijimos que y = uv , entonces podemos sustituir esa igualdad en lo que llevamos del proceso:
$\displaystyle uv=\int{udv}+\int{vdu}$
Que dicho y expresado de otra forma, esta igualdad la podemos invertir, es decir:
$\displaystyle \int{udv}+\int{vdu}=uv$
Y si ahora despejamos la primera integral, dejándola sola del miembro izquierdo, nos queda:
$\displaystyle \int{udv}=uv-\int{vdu}$
Que finalmente es la fórmula de integral por partes. 😎
Aplicaciones de las Integrales por Partes
Aunque las integrales por lo general tienen una aplicación real en nuestra vida diaria de forma implicita, aquí te explicamos cuáles son las aplicaciones donde las verás más seguidos en el mundo de la ingeniería.
En Física en el Cálculo del Trabajo y Energía
Sabemos que las integrales son una herramienta poderosa en matemáticas y en física, por ejemplo las integrales por partes se pueden emplear para el cálculo del trabajo y energía. Sabemos que el trabajo relizado por una fuerza variable se calcula a partir de una integral. Si la fuerza no es constante, la integración po partes puede ser muy útil para resolver integrales complejas. Por ejemplo:
Si la fuerza $\displaystyle F\left( x \right)$ depende de la posición $\displaystyle x$ , el trabajo $\displaystyle W$ se calcula como:
$\displaystyle W=\int\limits_{a}^{b}{{F\left( x \right)dx}}$
Si $\displaystyle {F\left( x \right)}$ es el producto de dos funciones, por ejemplo una fuerza y desplazamiento, la integración por partes puede simplificar el cálculo.
En el Momento de Inercia
En ingeneniería mecánica y estructural, los momentos de inercia son fundamentales para analizar la resistencia de materiales y estructuras. El momento de inercia I de un objeto se calcula como:
$\displaystyle I=\int{{{{r}^{2}}}}dm$
Donde $\displaystyle r$ es la distancia al eje de rotación y $\displaystyle dm$ es un elemento de masa. Si la distribución de masa es compleja, la integración por partes puede ayudar a resolver la integral.
Economía valor presente y valor futuro
En economía y finanzas, el valor presente y el valor futuro de flujos de efectivo se calculan mediante integrales. Por ejemplo
El valor presente $\displaystyle PV$ de un flujo de ingresos continuo $\displaystyle f\left( t \right)$ con una tasa de descuento $\displaystyle r$ es:
$\displaystyle PV=\int\limits_{0}^{T}{{f\left( t \right){{e}^{{-rt}}}dt}}$
si $\displaystyle f\left( t \right)$ es una función compleja, la integración por partes puede simplificar el cálculo.
✅ Reglas para la integración por partes
Ahora, antes de comenzar a resolver ejercicios donde apliquemos el método de por partes, es necesario tener en cuenta lo siguiente: Es muy probable que de la integral original nos quede una integral más, es decir; no en el primer intento de integración obtenemos el resultado, nos puede quedar otra integral más y seguiremos resolviendo.
Ahora, a pesar de que no existe una regla correcta para poder comprobar la variable adecuada en nuestra elección para u, o dv, hay algunos criterios funcionales que aplica en la mayor parte para las integrales por partes, estos criterios son.
1. Para integrales que tienen la forma:
$\displaystyle \int{p(x)\ln xdx}$
$\displaystyle \int{p(x)arcsenxdx}$
$\displaystyle \int{p(x)arccosxdx}$
$\displaystyle \int{p(x)arctanxdx}$
Donde p(x) es un polinomio, se recomienda siempre hacer U a la función trascendente, mientras que dv = p(x) [El polinomio]
2. Para integrales que tienen la forma:
$\displaystyle \int{p(x){{e}^{ax}}dx}$
$\displaystyle \int{p(x)senxdx}$
$\displaystyle \int{p(x)\cos xdx}$
En donde p(x) es un polinomio, se recomienda siempre hacer u = p(x), mientras que dv a la función trigonométrica o exponencial.
3. Apoyarse del acrónimo ILATE
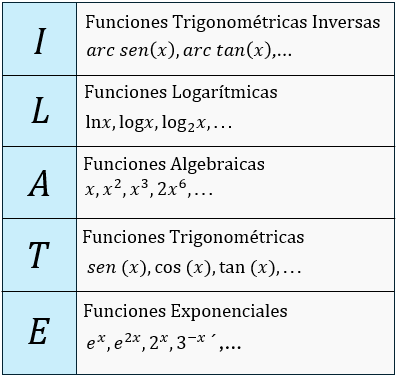
Dónde:
I = Inversas
L = Logarítmicas
A = Algebraicas
T = Trigonométricas
E = Exponenciales
Con este criterio podemos establecer para nosotros quien debe ser U, de izquierda a derecha, es decir primero buscamos que haya inversas, sino pasamos al segundo que es logarítmicas, luego algebraicas y así sucesivamente.
No hay mejor forma de entender a un tema que practicando, y más en este método. Así que veamos como resolver ejercicios de integración por partes paso a paso.
Ejercicios Resueltos de Integrales Por Partes
En los siguientes ejercicios se hará uso de las técnicas de integración por partes y de todo lo relacionado con ILATE para resolver diversos casos de integración. Prestar mucha atención porque es de vital importancia, en caso de tener dudas puedes consultar los videos que se han grabado en las diversas plataformas de nuestras redes sociales (tiktok, instagram y Youtube).
Solución:
Este tipo de integral no se puede resolver por el método de sustitución, pues se trata del producto de dos funciones, tanto "x" como el "sen(x)" se multiplican, entonces tenemos que recurrir a la integración por partes.
Necesitamos dos cosas, ¿quién será " u " ? y ¿quién será " dv " ?
Aplicando el acrónimo ILATE, vemos que no hay Inversas, no hay Logarítmicas, y lo que si tenemos es una función Algebraica, por lo que se puede tomar en cuenta para hacer a "u" a la función algebraica, si hacemos esto, tenemos:
$\displaystyle \begin{array}{*{20}{c}} {u=x} & {dv=sen(x)dx} \\ {du=dx} & {v=-\cos (x)} \end{array}$
Aplicando nuestra fórmula de integral por partes:
$\displaystyle \int{udv}=uv-\int{vdu}$
Es decir, que ya tenemos:
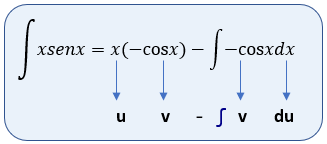 Ordenando, y resolviendo la integral del coseno x, qué es seno de x, entonces tenemos:
Ordenando, y resolviendo la integral del coseno x, qué es seno de x, entonces tenemos:
Resultado:

¿Tuviste problemas para entender la integral?, no te preocupes mira el video paso a paso 👇
| 🎵 Ver en TikTok | 📷 Ver en Instagram |
Solución:
Aplicando ILATE observamos que si tenemos una algebraica que es "x" y con eso partimos para nuestro cuadro de referencia:
$\displaystyle \begin{array}{*{20}{c}} {u=x} & {dv={{e}^{x}}dx} \\ {du=dx} & {v={{e}^{x}}} \end{array}$
Entonces resolvemos nuestra integral aplicando la fórmula por partes:
$\displaystyle \int{udv}=uv-\int{vdu}$
Entonces:
$\displaystyle =x{{e}^{x}}-\int{{{{e}^{x}}dx}}$
$\displaystyle =x{{e}^{x}}-{{e}^{x}}+C$
$\displaystyle ={{e}^{x}}(x-1)+C$
Por lo tanto, la integral buscada es:
Resultado:
\[
\boxed{\int x e^x \,dx = e^x (x - 1) + C}
\]
¿Tuviste problemas para entender la integral?, no te preocupes mira el video paso a paso 👇
| 🎵 Ver en TikTok | 📷 Ver en Instagram |
Solución:
Aplicando ILATE, tomamos \( \ln x \) como \( u \), ya que es una función logarítmica, y \( x dx \) como \( dv \):
\[
\begin{array}{c|c}
u = \ln x & dv = x \,dx \\
\hline
du = \frac{1}{x} dx & v = \frac{x^2}{2}
\end{array}
\]
Aplicamos la fórmula de integración por partes:
\[
\int u \, dv = uv - \int v \, du
\]
Sustituyendo los valores:
\[
\int x \ln x \,dx = \ln x \cdot \frac{x^2}{2} - \int \frac{x^2}{2} \cdot \frac{1}{x} dx
\]
\[
= \frac{x^2}{2} \ln x - \frac{1}{2} \int x \, dx
\]
Resolvemos la integral restante:
\[
\frac{x^2}{2} \ln x - \frac{1}{2} \cdot \frac{x^2}{2}
\]
\[
= \frac{x^2}{2} \ln x - \frac{x^2}{4} + C
\]
Resultado:
\[
\boxed{\int x \ln x \,dx = \frac{x^2}{2} \ln x - \frac{x^2}{4} + C}
\]
¿Tuviste problemas para entender la integral?, no te preocupes mira el video paso a paso 👇
| 🎵 Ver en TikTok | 📷 Ver en Instagram |
Solución:
Aplicando ILATE, tomamos \( \arctan(x) \) como \( u \), ya que es una función inversa, y \( dx \) como \( dv \):
\[
\begin{array}{c|c}
u = \arctan(x) & dv = dx \\
\hline
du = \frac{1}{1+x^2} dx & v = x
\end{array}
\]
Aplicamos la fórmula de integración por partes:
\[
\int u \, dv = uv - \int v \, du
\]
Sustituyendo los valores:
\[
\int \arctan(x) \,dx = x \arctan(x) - \int \frac{x}{1+x^2} dx
\]
La integral restante se resuelve con el cambio de variable:
Sea \( w = 1 + x^2 \), entonces \( dw = 2x dx \), por lo que:
\[
\int \frac{x}{1+x^2} dx = \frac{1}{2} \int \frac{dw}{w} = \frac{1}{2} \ln |1+x^2|
\]
Sustituyéndolo en la ecuación anterior:
\[
\int \arctan(x) \,dx = x \arctan(x) - \frac{1}{2} \ln |1+x^2| + C
\]
Resultado:
\[
\boxed{\int \arctan(x) \,dx = x \arctan(x) - \frac{1}{2} \ln |1+x^2| + C}
\]
¿Tuviste problemas para entender la integral?, no te preocupes mira el video paso a paso 👇
| 🎵 Ver en TikTok | 📷 Ver en Instagram |
Solución:
Aplicando ILATE, tomamos \( \ln x \) como \( u \), ya que es una función logarítmica, y \( \frac{dx}{x^2} \) como \( dv \):
\[
\begin{array}{c|c}
u = \ln x & dv = \frac{dx}{x^2} \\
\hline
du = \frac{dx}{x} & v = -\frac{1}{x}
\end{array}
\]
Aplicamos la fórmula de integración por partes:
\[
\int u \, dv = uv - \int v \, du
\]
Sustituyendo los valores:
\[
\int \frac{\ln x}{x^2} \,dx = \ln x \left(-\frac{1}{x} \right) - \int \left(-\frac{1}{x} \cdot \frac{dx}{x} \right)
\]
\[
= -\frac{\ln x}{x} + \int \frac{dx}{x^2}
\]
Resolvemos la integral restante:
\[
\int \frac{dx}{x^2} = -\frac{1}{x}
\]
Sustituyendo:
\[
-\frac{\ln x}{x} - \left(-\frac{1}{x} \right)
\]
\[
= -\frac{\ln x}{x} + \frac{1}{x} + C
\]
Resultado:
\[
\boxed{\int \frac{\ln x}{x^2} \,dx = \frac{1 - \ln x}{x} + C}
\]
¿Tuviste problemas para entender la integral?, no te preocupes mira el video paso a paso 👇
| 🎵 Ver en TikTok | 📷 Ver en Instagram |
Solución:
Aplicamos el método de integración por partes, eligiendo:
\[
\begin{array}{c|c}
u = x & dv = 2^x \,dx \\
\hline
du = dx & v = \frac{2^x}{\ln 2}
\end{array}
\]
Recordemos la fórmula de integración por partes:
\[
\int u \, dv = uv - \int v \, du
\]
Sustituyendo los valores:
\[
\int x 2^x \,dx = x \cdot \frac{2^x}{\ln 2} - \int \frac{2^x}{\ln 2} dx
\]
La integral restante se resuelve de forma directa:
\[
\int \frac{2^x}{\ln 2} dx = \frac{2^x}{(\ln 2)^2}
\]
Sustituyéndolo en la ecuación anterior:
\[
\int x 2^x \,dx = \frac{x 2^x}{\ln 2} - \frac{2^x}{(\ln 2)^2} + C
\]
Resultado:
\[
\boxed{\int x 2^x \,dx = \frac{x 2^x}{\ln 2} - \frac{2^x}{(\ln 2)^2} + C}
\]
¿Tuviste problemas para entender la integral?, no te preocupes mira el video paso a paso 👇
| 🎵 Ver en TikTok | 📷 Ver en Instagram |
Solución:
Para resolver esta integral aplicamos el método de integración por partes dos veces, utilizando la técnica de ecuaciones simultáneas.
Definimos:
\[
\begin{array}{c|c}
u = \sin x & dv = e^x dx \\
\hline
du = \cos x dx & v = e^x
\end{array}
\]
Aplicamos la fórmula de integración por partes:
\[
\int u \, dv = uv - \int v \, du
\]
Sustituyendo los valores:
\[
\int e^x \sin x \,dx = e^x \sin x - \int e^x \cos x \,dx
\]
Para resolver \(\displaystyle \int e^x \cos x \,dx\), aplicamos nuevamente integración por partes:
\[
\begin{array}{c|c}
u = \cos x & dv = e^x dx \\
\hline
du = -\sin x dx & v = e^x
\end{array}
\]
Aplicamos la fórmula:
\[
\int e^x \cos x \,dx = e^x \cos x - \int e^x (-\sin x) dx
\]
\[
= e^x \cos x + \int e^x \sin x \,dx
\]
Ahora tenemos la ecuación:
\[
I = e^x \sin x - (e^x \cos x + I)
\]
\[
I = e^x \sin x - e^x \cos x - I
\]
Sumamos \( I \) a ambos lados:
\[
2I = e^x (\sin x - \cos x)
\]
Despejamos \( I \):
\[
I = \frac{e^x (\sin x - \cos x)}{2}
\]
Resultado:
\[
\boxed{\int e^x \sin x \,dx = \frac{e^x (\sin x - \cos x)}{2} + C}
\]
¿Tuviste problemas para entender la integral?, no te preocupes mira el video paso a paso 👇
| 🎵 Ver en TikTok | 📷 Ver en Instagram |
Solución:
Si nos basamos nuevamente en el acrónimo ILATE , vemos que tenemos dos funciones en la integral, a x al cuadrado y a la exponencial elevado a la "x", entonces si seguimos la regla, lo primero que vamos a encontrar es a la algebraica, quien será nuestra "u" y la otra parte "dv" será para la exponencial, de esta forma:
$\displaystyle \begin{array}{*{20}{c}} {u={{x}^{2}}} & {dv={{e}^{x}}dx} \\ {du=2xdx} & {v={{e}^{x}}} \end{array}$
Es, decir que ya tenemos:
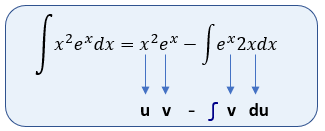
Sin embargo, aquí nos topamos con un caso diferente, existe otra integral por partes dentro de la misma integral por partes :O
Ordenamos y resolvemos dicha integral.
$\displaystyle \int{2x{{e}^{x}}dx}$
Nuevamente se trata de una integral por partes, entonces vamos a solucionarlo como lo hemos venido haciendo.
$\displaystyle \begin{array}{l}u=2x\\dv={{e}^{x}}dx\end{array}$
De esta nueva integral, nos queda:
$\displaystyle \begin{array}{*{20}{c}} {u=2x} & {dv={{e}^{x}}dx} \\ {du=2dx} & {v={{e}^{x}}} \end{array}$
Por lo que:
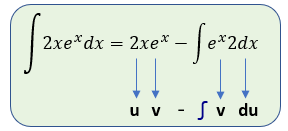
Resolviendo la segunda integral nos queda:
$\displaystyle \int{2x{{e}^{x}}dx=2x{{e}^{x}}-2{{e}^{x}}}$
Ahora juntando nuestra última integral, con la anterior. Nos queda:
Resultado:
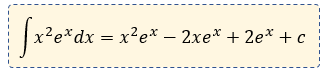
¿Tuviste problemas para entender la integral?, no te preocupes mira el video paso a paso 👇
| 🎵 Ver en TikTok | 📷 Ver en Instagram |
Solución:
Una de las integrales más nombradas dentro de la integración por partes, es la integral de la secante cúbica, ésta integral de pontencia none, se debe hacer por partes. Así que la vamos a resolver sin problemas.
Primero aplicaremos lo siguiente:
$\displaystyle \int{{{\sec }^{3}}xdx=}\int{{{\sec }^{2}}x\sec xdx}$
Por identidad trigonométrica, sabemos que:
$\displaystyle {{\sec }^{2}}x={{\tan }^{2}}x+1$
Sustituyendo en nuestra integral.
$\displaystyle \int{\left( {{\tan }^{2}}x+1 \right)\sec xdx}$
Aplicando propiedad distributiva, tenemos que:
$\displaystyle \int{{{\tan }^{2}}x}\sec xdx+\int{\sec x}dx$
La segunda integral es la más sencilla, porque es una integral directa. Ahora debemos realizar la primera. Y nos enfocaremos en ello.
Para esta integral por parte, hacemos:
$\displaystyle \begin{array}{*{20}{c}} {u=\tan x} & {dv=\tan x\sec xdx} \\ {du={{{\sec }}^{2}}xdx} & {v=\sec x} \end{array}$
Es decir que ya tenemos:
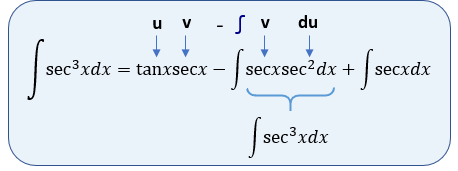
Si observamos, vemos que en nuestro desarrollo de la integral obtenemos exactamente el resultado de la integral que estamos resolviendo, entonces vamos a realizar lo siguiente: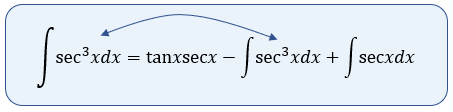 Si realizamos el despeje, tenemos entonces que:
Si realizamos el despeje, tenemos entonces que:
$\displaystyle \int{{{\sec }^{3}}xdx}+\int{{{\sec }^{3}}xdx}=\tan x\sec x+\int{\sec xdx}$
Las integrales del miembro izquierdo se suman, y en el miembro derecho integramos a secante de "x". Esto daría:
$\displaystyle 2\int{{{\sec }^{3}}xdx}=\tan x\sec x+\ln (\tan x+\sec x)+c$
Y finalmente, despejamos a la integral de secante cúbica, por lo que el dos que multiplica a la integral, pasará a dividir al segundo miembro, de esta forma:
Resultado:
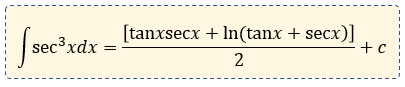
¿Tuviste problemas para entender la integral?, no te preocupes mira el video paso a paso 👇
| 🎵 Ver en TikTok | 📷 Ver en Instagram |
¿Te gustó este contenido?
Únete a nuestra comunidad en WhatsApp o Telegram para recibir nuevos proyectos, tutoriales y noticias exclusivas.
Deja una respuesta

Estos temas te pueden interesar