Ley de Faraday - Ejercicios Resueltos

La ley de Faraday o ley del electromagnetismo se dedujo a partir de los experimentos de Michael Faraday donde enunció lo siguiente:

? Fórmula de la Ley de Faraday

La ley de Faraday se expresa de la siguiente manera, la intensidad de la corriente inducida en un circuito es directamente proporcional a la rapidez con que cambia el flujo magnético, que matemáticamente la podemos observar de la siguiente manera:

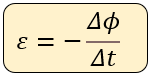
o de otra forma:

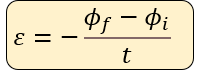
Dónde:

ε = fem media inducida expresada en volts (V)

φf = Flujo magnético final medida en webers (Wb)

φi = Flujo magnético inicial calculado en webers (Wb)

t = tiempo que se realiza la variación del flujo, medido en segundos(s)

Nota: El signo ( - ) de la ecuación se debe a la posición existente entre la fem inducida y la variación de flujo que la produce (ley de Lenz).

Cuando se trata de una bobina que tiene N número de vueltas o espiras, la expresión matemática para calcular la fem inducida es la siguiente:

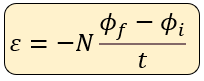
Ahora, cuando queremos calcular la fem inducida en un conductor recto de longitud L que se desplaza con una magnitud de velocidad v en forma perpendicular a un campo de inducción magnética B se utiliza la expresión:

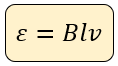
? Ejemplos Resueltos de la Ley de Faraday

Ahora veamos algunos ejemplos para entender mucho mejor este tema, es importante recordar que para entender la ley de Faraday es importante tener conocimiento de la inducción electromagnética y de la ley de lenz.

Solución:

Si leemos bien el problema, nos damos cuenta que habla de un conductor rectilíneo, por lo cual aplicaremos la fórmula que relaciona al campo magnético, la longitud y su velocidad, entonces debemos anotar nuestros datos:

Datos:

l = 10 cm = 0.1 m

B =0.4 T

v = 3.4 m/s

Ahora si podemos aplicar la siguiente fórmula:

$\displaystyle \varepsilon =Blv$

Sustituyendo:

$\displaystyle \varepsilon =Blv=\left( {0.4T} \right)\left( {0.1m} \right)\left( {3.4\frac{m}{s}} \right)=0.136V$

Por lo que la fem inducida es de 0.136 V

Solución:

A diferencia del ejemplo 1, en este ejemplo hablamos no de un conductor, sino más bien de una bobina pero tiene 600 espiras, lo que implica que es una fórmula donde hay una "N" de número de vueltos.

Entonces, anotemos los datos:

Datos:

N = 600 vueltas

t = 8x10^-2 s

Φi = 1.8x10^-4 Wb

Φf = 9x10^-4 Wb

La fórmula a utilizar será la siguiente:

$\displaystyle \varepsilon =-N\frac{{{{\phi }_{f}}-{{\phi }_{i}}}}{t}$

sustituyendo los datos en la fórmula

$\displaystyle \varepsilon =-600\left( {\frac{{9x{{{10}}^{{-4}}}Wb-1.8x{{{10}}^{{-4}}}Wb}}{{8x{{{10}}^{{-2}}}s}}} \right)=-5.4V$

Lo que genera un valor de -5.4 V

Solución:

El problema habla de una espira, por lo que utilizaremos la fórmula donde no existe "N" porque no es una bobina, sino solo una espira. Entonces anotemos nuestros datos:

Datos:

Φi = 2x10^-3 Wb

Φf = 7x10^-3 Wb

t = 0.04 s

La fórmula que utilizaremos, será la siguiente:

$\displaystyle \varepsilon =-\frac{{{{\phi }_{f}}-{{\phi }_{i}}}}{t}$

Sustituyendo estos datos en nuestra fórmula, obtenemos:

$\displaystyle \varepsilon =-\left( {\frac{{7x{{{10}}^{{-3}}}Wb-2x{{{10}}^{{-3}}}Wb}}{{0.04s}}} \right)=-0.125V$

Obtenemos un valor de -0.125 V de fem media inducida.

Nota: En algunos libros, o autores, la ley de Faraday también se le puede llamar como la Ley de Faraday - Neumann