Problema 4 de Dilatación Superficial

Con este cuarto problema de Dilatación Superficial , podemos dejar por concluido que los problemas de dilatación son muy sencillos y requieren prestar atención a los enunciados de los ejercicios para no tener ningún problema con ellos, en el siguiente problema propuesto nuevamente se deja para que el alumno corrobore sus resultados y entienda la solución del mismo 😊👇

Nivel de Dificultad: ⭐⭐⭐⭐

Problema 6. Una moneda fabricada con níquel puro, está a una temperatura ambiente de 20°C, al ser llevada a un horno, ella sufre un aumento del 1% en el área de su superficie. ¿Cuál es la temperatura del horno? , el coeficiente de dilatación superficial del níquel es de 25x10^(-6) °C ¯¹

Problema de dilatación superficial

Solución:

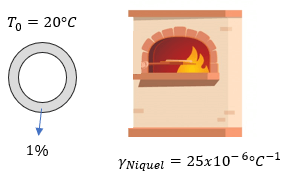
Si observamos el problema, nos daremos cuenta que no nos proporcionan un área inicial, y tampoco un área final, aún así nos pide el problema encontrar la temperatura final. ¿Cómo lo resolveríamos si no tenemos áreas?, pero también debemos comprender que gran parte de este problema nos comenta que la moneda de níquel sufre una alteración del 1% en su superficie (después de ser expuesta a la temperatura final). En términos más simples, se alteró 1% de su superficie inicial. Este dato nos ayudará a comprender mejor el problema.

Obtener la temperatura final del horno

Datos:

$\displaystyle {{T}_{0}}=20{}^\circ C$

$\displaystyle {{\gamma }_{Niquel}}=25x{{10}^{-6}}{}^\circ {{C}^{-1}}$

$\displaystyle {{A}_{f}}-{{A}_{0}}=0.01{{A}_{0}}$

Hemos agregado un nuevo dato que puede ser extraño para usted. Pero analicemos: La diferencia de área no es más que el 1% del área inicial. Es por eso que la hemos agregado como dato. Pues lo único que sabemos es que el área inicial se altero 1% del área final. Teniendo en cuenta esto, podemos nuevamente colocar nuestra fórmula:

$\displaystyle {{A}_{f}}={{A}_{0}}[1+\gamma \left( {{T}_{f}}-{{T}_{0}} \right)]$

En el ejercicio resuelto número 3 de Dilatación Superficial, despejamos a la temperatura final de la fórmula, quedando así:

$\displaystyle {{T}_{f}}=\frac{{{A}_{f}}-{{A}_{0}}}{\gamma {{A}_{0}}}+{{T}_{0}}$

Sustituyendo nuestros datos en la fórmula de la temperatura final, obtenemos:

$\displaystyle {{T}_{f}}=\frac{0.01{{A}_{0}}}{\left( 25x{{10}^{-6}}{}^\circ {{C}^{-1}} \right){{A}_{0}}}+20{}^\circ C$

Simplificando el numerador y denominador, esto nos queda:

$\displaystyle {{T}_{f}}=\frac{0.01}{25x{{10}^{-6}}{}^\circ {{C}^{-1}}}+20{}^\circ C$

Realizando la división correspondiente

$\displaystyle {{T}_{f}}=400{}^\circ C+20{}^\circ C$

Finalmente sumamos:

$\displaystyle {{T}_{f}}=420{}^\circ C$

Qué vendría a ser 420 °C de temperatura final en el horno.

Resultado:

$\displaystyle {{T}_{f}}=420{}^\circ C$

Deja una respuesta Cancelar la respuesta