Solución Problema 1 de la Ley General del Estado Gaseoso

En este ejemplo de los problemas resueltos para ejercicios de práctica del tema de La ley general del estado gaseoso, es importante tener en cuenta el uso correcto de la fórmula, es por eso que se realizan los ejercicios paso a paso con su solución correspondiente. Recuerde que con este tipo de ejemplos el alumno podrá corroborar su respuesta y verificar si ha llegado al mismo resultado. 😊👇

Nivel de Dificultad: ⭐⭐

Problema 3.- Calcular el volumen que ocupará un gas en condiciones normales, si a una presión de 940 mm de Hg y 23°C su volumen es de 184 cm³

Problema de la ley general del estado gaseoso

Solución:

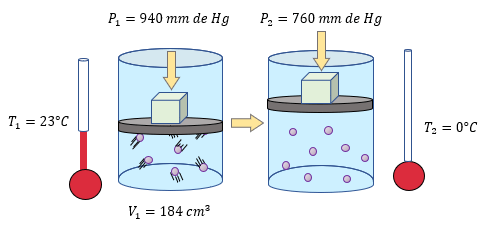
Al analizar el problema, vemos que nos comenta que el volumen del gas está en condiciones normales, esto quiere decir que está a una temperatura de 0°C, o sea a 273 K, y que mantiene una presión de una atmósfera, que es equivalente a 760 mm de Hg, entonces tenemos dos datos más que tenemos que agregar a la solución del ejercicio.

Obtener el volumen final

Datos:

$\displaystyle {{P}_{1}}=940mmdeHg$

$\displaystyle {{T}_{1}}=23{}^\circ C+273=296K$

$\displaystyle {{V}_{1}}=184c{{m}^{3}}$

$\displaystyle {{P}_{2}}=760mmdeHg$

$\displaystyle {{T}_{2}}=0{}^\circ C+273=273K$

Es importante recordar que tanto la presión 2 y la temperatura 2 se fueron colocando de esta manera porque el gas se encuentra en condiciones normales.

a) Obtener el volumen final

Si la fórmula de la ley general del estado gaseoso es la siguiente:

$\displaystyle \frac{{{P}_{1}}{{V}_{1}}}{{{T}_{1}}}=\frac{{{P}_{2}}{{V}_{2}}}{{{T}_{2}}}$

Despejamos a "V2" de la fórmula:

$\displaystyle {{V}_{2}}=\frac{{{P}_{1}}{{V}_{1}}{{T}_{2}}}{{{P}_{2}}{{T}_{1}}}$

Si tienes problemas de despeje, puedes visitar el post de Aprende a despejar fórmulas

Ahora si podemos sustituir nuestros datos en la fórmula:

$\displaystyle {{V}_{2}}=\frac{{{P}_{1}}{{V}_{1}}{{T}_{2}}}{{{P}_{2}}{{T}_{1}}}=\frac{\left( 940mmdeHg \right)\left( 184c{{m}^{3}} \right)\left( 273K \right)}{\left( 760mmdeHg \right)\left( 296K \right)}=209.89c{{m}^{3}}$

Por lo que nuestro volumen final es de 209.89 cm³

Resultado:

$\displaystyle {{V}_{2}}=209.89c{{m}^{3}}$

2 Comentarios Publicados

Andres Felipe Fonseca Ortiz dice:

4 junio, 2023 a las 8:46 pm

que pena encuentro un error en la Temperatura 1 es 196 no 296 y esto cambia totalmente el resultado que en verdad es 316,98 agradezco su respuesta pronta muchas gracias y feliz noche

Responder
1. Carlos julián dice:
  
  24 junio, 2023 a las 8:51 am
  
  ¿De dónde sacas 196?
  
  Responder

Deja una respuesta Cancelar la respuesta