Solución Problema 1 de Movimiento Circular

En este ejemplo de los problemas resueltos para ejercicios de práctica del tema de Movimiento Circular Uniformemente Acelerado, es importante tener en cuenta el uso correcto de la fórmula, es por eso que se realizan los ejercicios paso a paso con su solución correspondiente. Recuerde que con este tipo de ejemplos el alumno podrá corroborar su respuesta y verificar si ha llegado al mismo resultado. 😊👇

Nivel de Dificultad: ⭐⭐

Solución:

El problema es muy sencillo, puesto que nos proporcionan los datos necesarios para emplear la fórmula de velocidad angular final, si observamos contamos con velocidad angular inicial, el tiempo y la aceleración angular. Entonces ¿cómo procedemos a resolver el problema?

• Obtener la velocidad angular final

Datos:

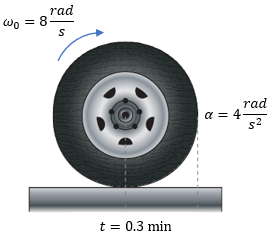
$\displaystyle {{\omega }_{0}}=8\frac{rad}{s}$

$\displaystyle \alpha =4\frac{rad}{{{s}^{2}}}$

$\displaystyle t=0.3\min $

a) Obteniendo la velocidad angular final

Vamos a emplear la siguiente fórmula, ya que es la que mejor se adecua a nuestros datos:

$\displaystyle {{\omega }_{f}}={{\omega }_{0}}+\alpha t$

Antes de sustituir nuestros datos en la fórmula, es importante que pasemos a segundos los minutos, usando el factor de conversión.

$\displaystyle t=0.3\min \left( \frac{60s}{1\min } \right)=18s$

Ahora si podemos sustituir nuestros datos en la fórmula:

$\displaystyle {{\omega }_{f}}=8\frac{rad}{s}+\left( 4\frac{rad}{{{s}^{2}}} \right)\left( 18s \right)$

$\displaystyle {{\omega }_{f}}=8\frac{rad}{s}+72\frac{rad}{s}$

Finalmente, sumamos:

$\displaystyle {{\omega }_{f}}=80\frac{rad}{s}$

Es decir que la velocidad angular final es de 80 rad/s

Resultado:

$\displaystyle {{\omega }_{f}}=80\frac{rad}{s}$