Conversión de Unidades - Ejercicios Resueltos

¿Qué tal amig@s?, hoy hablaremos sobre la conversión de unidades en Física, No se puede realizar una conversión de unidades, si no tenemos ni la mínima idea de donde vienen las unidades, cuales son, o incluso qué tipos de unidades existen, así que primero las iremos explicando poco a poco y después empezaremos a realizar varios ejemplos resueltos para que finalmente aprendas a convertir unidades sin problemas. 😀

Sistema Métrico Decimal

Este sistema fue creado en una convención mundial de ciencia celebrada en París, Francia; en el siglo XVII para ser exactos, allá por el año 1795. Este sistema fue muy importante porque fue el primer patrón que existió para las unidades de medidas, entre ellas se encuentras las unidades como el metro, el kilogramo-peso y el litro. ¿Qué usaron para definir estas unidades?, pues aquí viene lo importante, para definir dichas unidades, utilizaron la dimensión de la tierra y la densidad del agua.

Después de realizar dicho acuerdo con la longitud, ésta misma sirvió de ejemplo para obtener las demás unidades. Es por eso que la palabra metro significa "medida".

Una característica importante de éste sistema, fue sin duda la división decimal que tenía; por ejemplo el uso de los prefijos como: deci, centi o mili.

• Decímetro = décima parte del metro
• Centímetro = centésima para del metro
• Milímetro = la milésima parte del metro

Por otra parte tenemos también a los prefijos como: deca, hecto, kilo.

• Decámetro = diez veces el valor del metro
• Hectómetro = cien veces el valor del metro
• Kilómetro = mil veces el valor del metro

Sistema Cegesimal o CGS

Después del sistema métrico decimal, y con el avance de la Física en el siglo XVIII, se realizó el Congreso Internacional de los Electricistas, donde nuevamente se llevó a cabo en París, Francia. Después de grandes acuerdos en el congreso internacional y liderado por el físico alemán Karl Gauss, se propuso el Sistema Cegesimal o también conocido por sus siglas CGS , en dicho sistema se establece la longitud para el centímetro, la masa para el gramo y el segundo para el tiempo.

Cabe mencionar que en ese tiempo donde la física empezaba a tener grandes avances históricos, ya se tenía claro que el peso y la masa eran dos magnitudes muy diferentes, pues ya había estudio sobre las leyes de Newton y sobre la gravitación universal 

Sistema MKS

Pasaron cerca de 50 años, para que el Congreso Internacional de los Electricistas se llevara a cabo en Bruselas, Bélgica, en donde un ingeniero Italiano de nombre Giovanni Giorgi propone su sistema MKS cuyas iniciales son (Metro - Kilogramo - Segundo).

Sistema Internacional de Unidades (SI)

El avance de la ciencia era evidente para el siglo XIX, y no hace muchos años en la ciudad de Ginebra, Suiza. Pero era necesario actualizar las unidades de medida, es por ello que surge el Sistema Internacional de Unidades (SI), este sistema tiene su esencia y base en el sistema MKS, solo que a excepción del MKS este sistema establece siete magnitudes fundamentales.

• Longitud → Metro
• Masa → Kilogramo
• Tiempo → Segundo
• Temperatura → Kelvin
• Intensidad de Corriente Eléctrica → Ampere
• Intensidad Luminosa → Candela
• Cantidad de Sustancia → Mol

Prefijos Utilizados para el Sistema Internacional

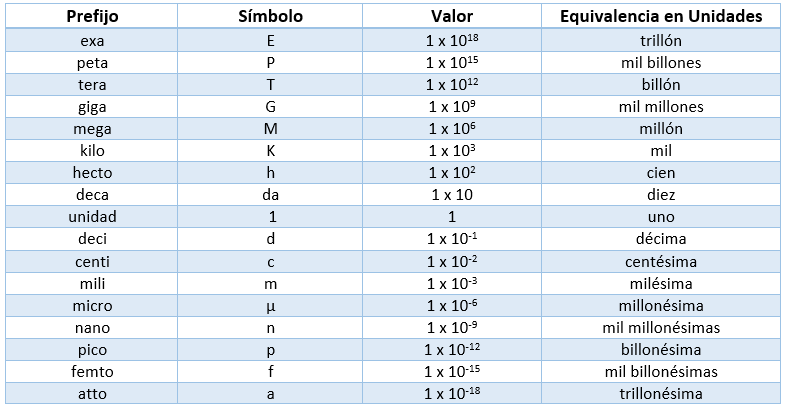
Magnitudes Derivadas

Las magnitudes derivadas son aquellas magnitudes que se pueden obtener a partir de otras magnitudes físicas, es muy común obtener magnitudes derivadas al multiplicar o dividir las magnitudes fundamentales. Veamos un ejemplo muy sencillo:

Longitud/Tiempo = m/s → (metro / segundo)

Obtenemos la velocidad a través la longitud y el tiempo, es decir a partir de las magnitudes fundamentales.

Y así podemos encontrarnos con varias magnitudes derivadas, tales como la aceleración, fuerza, trabajo, energía, presión, potencia, densidad, etc. En la siguiente imagen, se puede observar mucho mejor.

Ejercicios Resueltos de Conversión de Unidades

Es importante en Física aprender a convertir las unidades, el poder transformar unidades de un sistema a otro. Así que antes de comenzar a resolver ejercicios, veamos una tabla comparativa de equivalencias, tal como se muestra:

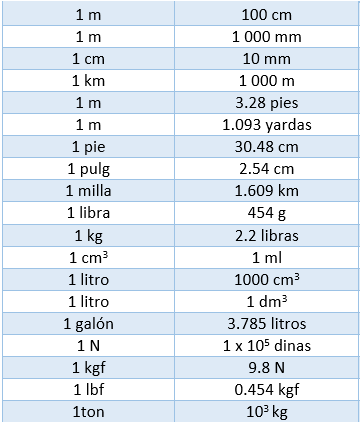
Veamos la siguiente conversión de unidades.

Solución: Lo primero que haremos será analizar cuántos metros caben en 1 kilómetro, y si observamos la tabla, vemos que cabe exactamente 1 000 metros, entonces aplicamos nuestro factor de conversión de tal manera que quede expresado de la siguiente manera:

$\displaystyle 4km\left( \frac{1000m}{1km} \right)=4000m$

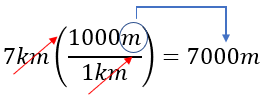
Solución: Para convertir 7 pies a metros, necesitamos verificar nuestra tabla, y observar el factor de conversión que utilizaremos. En este caso sería; 1 metro = 3.28 pies (ft)

$\displaystyle 7pies\left( \frac{1m}{3.28pies} \right)=2.134m$

Veamos el mismo ejemplo de forma gráfica (para darnos cuenta como se simplifican las unidades de medida).

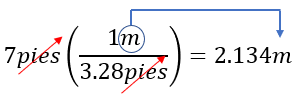
Solución: En este caso tenemos velocidad en unidades de longitud y tiempo, para ello veamos los recursos que tenemos para identificar los factores de conversión posibles. Sabemos que:

1 km = 1000 m

1 hr = 60 min

1 min = 60 s

Con estos datos podemos obtener la conversión sin problemas, ejemplo:

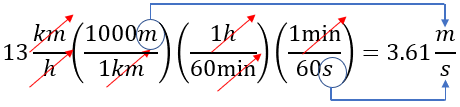
$\displaystyle 13\frac{km}{h}\left( \frac{1000m}{1km} \right)\left( \frac{1h}{60\min } \right)\left( \frac{1\min }{60s} \right)=3.61\frac{m}{s}$

Aquí veamos la solución más claro, en caso que tengas dudas:

Solución: En este caso, necesitamos observar si hay alguna relación directa con el factor de conversión con galones y centímetros cúbicos, pero vemos qué no hay (en nuestra tabla), entonces tenemos que guiarnos con algo que nos pueda ayudar a relacionar dichas medidas, por ejemplo. Sabemos que:

1 Galón = 3.785 litros

1 Litro = 1000 cm³

Con estos datos, podemos obtener la respuesta. Entonces colocamos.

$\displaystyle 7gal\left( \frac{3.785l}{1gal} \right)\left( \frac{1000c{{m}^{3}}}{1l} \right)=26495c{{m}^{3}}$

Veamos más claro la conversión:

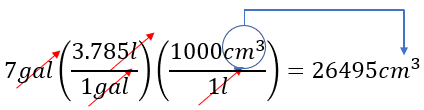
Solución: Al igual que el ejemplo 3, tenemos que relacionar los factores de conversión disponibles para realizar nuestro cálculo de manera correcta, para ello comenzamos con utilizar:

1 milla = 1.609 km

1 km = 1000 m

1 hr = 60 min

1 min = 60 s

Ahora si podemos realizar la conversión

$\displaystyle 8\frac{millas}{h}\left( \frac{1.609km}{1milla} \right)\left( \frac{1000m}{1km} \right)\left( \frac{1h}{60\min } \right)\left( \frac{1\min }{60s} \right)=3.57\frac{m}{s}$

Para ver más clara la conversión, veamos la imagen:

Solución: 

Primero, recordemos el siguiente factor de conversión.

$\displaystyle 1cm=0.3937in$

Entonces:

$\displaystyle 26in=26in\left( {\frac{{1cm}}{{0.3937in}}} \right)=66.04cm$

La diagonal de la pantalla mide 66.04 cm.

Solución:

Recordando que:

$\displaystyle 1in=2.54cm$

Entonces:

$\displaystyle 12cm=12cm\left( {\frac{{1in}}{{2.54cm}}} \right)=4.724in$

El diámtro de los discos es de 4.724 in

Solución: 

Recordando que:

$\displaystyle 1ft=0.3048m$

Entonces:

$\displaystyle 30000ft=30000ft\left( {\frac{{0.3048m}}{{1ft}}} \right)=9144m$

Solución: 

Recordando que:

$\displaystyle 1km=0.621371mi$

Entonces:

$\displaystyle 6370km=6370km\left( {\frac{{0.621371mi}}{{1km}}} \right)=3958.13mi$

El diámetro de la tierra es de 3958.13 millas

Solución:

Recordando que:

$\displaystyle 1cm=0.3937in$

$\displaystyle 1g=0.035274oz$

Empecemos por convertir las dimensiones de longitud del teléfono celular:

$\displaystyle 12.38cm=12.39cm\left( {\frac{{0.3937in}}{{1cm}}} \right)=4.874in$

$\displaystyle 5.86cm=5.86cm\left( {\frac{{0.3937in}}{{1cm}}} \right)=2.307in$

$\displaystyle 0.76cm=0.76cm\left( {\frac{{0.3937in}}{{1cm}}} \right)=0.299in$

Ahora el de la masa:

$\displaystyle 112g=112g\left( {\frac{{0.03574oz}}{{1g}}} \right)=3.95oz$

Las dimensiones del disco serían 4.874 in x 2.307 in x 0.299 in y tiene una masa de 3.95 oz.

Solución:

Recordando que:

$ \displaystyle 1km=0.621371mi$

Entonces:

$\displaystyle \text{8}\text{.33 km = 8}\text{.33 km}\left( {\frac{{\text{0}\text{.62371 mi}}}{{1km}}} \right)\text{=5}\text{.176 mi}$

Por lo tanto, 8.33 km equivalen a 5.176 mi.

Solución:

Recordando que:

$\displaystyle \text{1 gal = 3}\text{.785}l$

Entonces:

$\displaystyle \text{19}\text{.3 gal = 19}\text{.3 gal}\left( {\frac{{\text{3}\text{.785 l}}}{{1gal}}} \right)=73.05l$

Por lo tanto, 19.3 gal equivalen a 73.05 l.

Solución:

Recordando que:

$\displaystyle \text{1 kg = 0}\text{.06852 slug}$

Entonces:

$\displaystyle \text{45 kg = 45 kg}\left( {\frac{{\text{0}\text{.06852 slug}}}{{\text{1 kg}}}} \right)\text{= 3}\text{.0834 slug}$

Por lo tanto, 45 kg equivalen a 3.0834 slug.

Solución:

Recordando que:

$\displaystyle \text{1cm = 0}\text{.0328 ft}$

Entonces:

$\displaystyle \text{18 cm = 18 cm}\left( {\frac{{\text{0}\text{.0328 ft}}}{{\text{1 cm}}}} \right)\text{= 0}\text{.5904 ft}$

Por lo tanto, 18 cm equivalen a 0.5904 ft.

Solución:

Recordando que:

$\displaystyle \text{1in = 0}\text{.0254 m}$

Entonces:

$\displaystyle \text{27}\text{.11 in = 27}\text{.11 in}\left( {\frac{{\text{0}\text{.0254 m}}}{{\text{1 in}}}} \right)\text{= 0}\text{.6885 in}$

Por lo tanto, 27.11 in equivalen a 0.6885 in.

Solución:

Recordando que:

$\displaystyle \text{1 oz = 0}\text{.0283495 kg}$

Entonces:

$\displaystyle \text{125 oz = 125 oz}\left( {\frac{{\text{0}\text{.0283495 kg}}}{{\text{1 oz}}}} \right)\text{= 3}\text{.5436 kg}$

Por lo tanto, 125 oz equivalen a 3.5436 kg.

Solución:

Recordando que:

$\displaystyle \begin{array}{l}\text{1 bbl = 42 gal}\\\text{1gal = 3}\text{.78541 d}{{\text{m}}^{3}}\end{array}$

Entonces:

$\displaystyle \text{47}\text{.5 bbl = 47}\text{.5 bbl}\left( {\frac{{\text{42 gal}}}{{1bbl}}} \right)\left( {\frac{{3.78541d{{m}^{3}}}}{{1gal}}} \right)=7551.893d{{m}^{3}}$

Por lo tanto, 47.5 bbl equivalen a 7551.893 dm³

Listo!!! ¿Fácil? Ahora es momento de practicar.

Ejercicios para Practicar de Conversión de Unidades

Resuelta los siguientes ejercicios y compare sus resultados, para ver los procedimientos y resultados de click en el texto "Ver Solución" ??

? Ver Solución 

? Ver Solución 

? Ver Solución 

? Ver Solución 

? Ver Solución 

? Ver Solución 

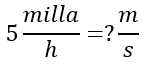
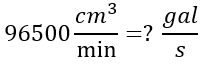
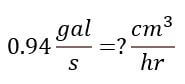
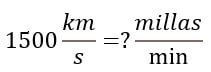
Examen de Conversión de Unidades

Llegó el moento de probar tu habilidad, resuelve el examen gratuito de 10 preguntas de conversión de unidades: