Análisis Dimensional - Ejercicios Resueltos

En física es importante que, al introducirse en este mundo, tengamos en cuenta al análisis dimensional, pero. ¿Qué es el análisis dimensional? Bien, el análisis dimensional es una forma de representación para poder observar la dependencia entre una magnitud (unidad) derivada y las magnitudes (unidades) fundamentales, que son formadas por un monomio y a su vez representadas por el producto de los símbolos de las (unidades) fundamentales elevados a diversas potencias denominadas dimensiones. Aunque quizá esto te suene confuso, veamos la siguiente ecuación o fórmula dimensional, para entender paso a paso de que va este tema, ¡¡No es complicado!!

Ecuación o Fórmula Dimensional

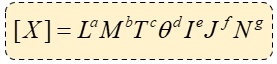
Dónde:

X = Símbolo de la magnitud X.

[X] = Dimensiones de la magnitud (unidad) X.

L = Símbolo de la magnitud (unidad) de longitud.

a = Dimensión de X respecto de la longitud.

M = Símbolo de la magnitud (unidad) de masa.

b = Dimensión de X respecto de la masa.

T = Símbolo de la magnitud (unidad) de tiempo.

c = Dimensión de X respecto del tiempo.

Θ = Símbolo de la magnitud (unidad) de temperatura.

d = Dimensión de X respecto de la temperatura.

I = Símbolo de la magnitud (unidad) de intensidad de corriente eléctrica.

e = Dimensión de X respecto de la intensidad de corriente eléctrica.

J = Símbolo de la magnitud (unidad) de intensidad luminosa.

f = Dimensión de X respecto de la intensidad luminosa.

N = Símbolo de la magnitud (unidad) de cantidad de sustancia.

g = Dimensión de X respecto de la cantidad de sustancia.

Esto nos da entender lo siguiente:

Si A: área ⇒ [A] ⇒ L² ⇒ el área se mide en m²

Si V: volumen ⇒ [V] = L³ ⇒ el volumen se mide en m³

Si D: densidad ⇒ [D] = masa/volumen ⇒ [D] = M/L³ = ML³

Sistema Internacional de Unidades

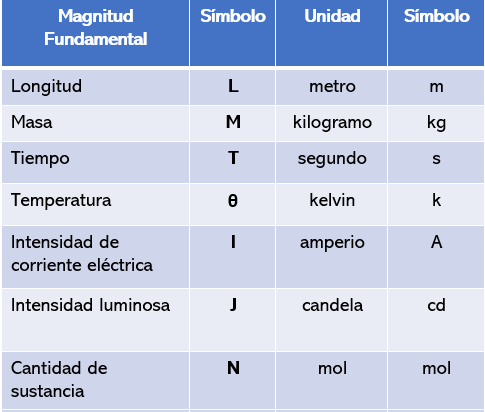
Observemos que cada magnitud fundamental, posee una representación (símbolo), así como la unidad y también el símbolo de dicha unidad. Para entenderlo mucho mejor veamos la siguiente tabla de unidades.

Principio de Homogeneidad Dimensional

Uno de los principios fundamentales en el análisis dimensional, es entender que en toda igualdad matemática o fórmula física que expresa la relación entre las diferentes magnitudes físicas, las dimensiones en el primer y segundo miembro, debe ser iguales, es decir, que se debe cumplir lo siguiente:

Si una fórmula física es correcta, todos los términos de la fórmula son dimensionalmente iguales, esto quiere decir por ejemplo que si tenemos la fórmula de la distancia del movimiento rectilíneo uniforme, entonces:

O sea que cada término separado es igual al otro término respecto a sus unidades, si estamos hablando de distancia, entonces todas las unidades nos darán distancia. El objetivo principal del análisis dimensional, lo podemos ver de la siguiente forma:

1. Nos ayuda a expresar las magnitudes derivadas en función de las magnitudes fundamentales
2. Comprobar la veracidad de las fórmulas físicas mediante el principio homogeneidad dimensional.
3. Determinar fórmulas físicas empíricas a partir de datos experimentales obtenidos en el laboratorio.

Tabla de las dimensiones principales de magnitudes físicas

Para ayudarnos a resolver ejercicios más adelante, veamos la siguiente tabla de dimensiones principales:

Para entender mucho mejor este concepto del análisis dimensional, veamos algunos ejemplos.

Ejemplos Resueltos de Análisis Dimensional

Solución:

Para poder darle solución a este problema, veamos el principio de homogeneidad dimensional, es decir:

$\displaystyle [KF]=[mv]$

Separando:

$\displaystyle [K][F]=[m][v]$

Revisando nuestra tabla de magnitudes físicas y sustituyendo:

$\displaystyle [K]ML{{T}^{{-2}}}=ML{{T}^{{-1}}}$

Despejando

$\displaystyle [K]=\frac{{ML{{T}^{{-1}}}}}{{ML{{T}^{{-2}}}}}={{T}^{{-1-(-2)}}}={{T}^{{-1+2}}}=T$

Observamos que K representa al tiempo.

Solución:

Veamos el principio de homogeneidad y observar como quedará nuestra fórmula:

$\displaystyle [Kv]=[Ft]$

Separando:

$\displaystyle [K][v]=[F][t]$

Revisamos nuevamente nuestra tabla de magnitudes físicas:

$\displaystyle [K]L{{T}^{{-1}}}=ML{{T}^{{-2}}}T$

Despejando:

$\displaystyle [K]=\frac{{ML{{T}^{{-2}}}T}}{{L{{T}^{{-1}}}}}=\frac{{M{{T}^{{-2+1}}}}}{{{{T}^{{-1}}}}}=\frac{{M{{T}^{{-1}}}}}{{{{T}^{{-1}}}}}=M$

Observamos que K representa a la masa.

Solución:

Por principio de homogeneidad dimensional, tenemos:

$\displaystyle [KF]=[m{{v}^{2}}]$

Separamos:

$\displaystyle [K][F]=[m][{{v}^{2}}]$

Buscamos nuestra tabla de magnitudes físicas:

$\displaystyle [K]ML{{T}^{{-2}}}=M{{L}^{2}}{{T}^{{-2}}}$

A simple vista observamos que nuestro resultado será:

$\displaystyle [K]=\frac{{M{{L}^{2}}{{T}^{{-2}}}}}{{ML{{T}^{{-2}}}}}=L$

Y esto nos conduce a decir que K representa a la longitud