Movimiento Rectilíneo Uniformemente Acelerado - Ejercicios Resueltos

Después de haber estudiado la velocidad media y el movimiento rectilíneo uniforme (MRU) es importante comenzar a estudiar al MRUA (Movimiento Rectilíneo Uniformemente Acelerado), para entender por completo el comportamiento de la velocidad y la aceleración, pero seguramente nos preguntamos ahora mismo ¿qué es el Movimiento Rectilíneo Uniformemente Acelerado?, pues bien comencemos 😀

Decimos que una partícula tiene movimiento rectilíneo uniformemente variado o acelerado (MRUA) cuando su trayectoria es rectilínea y la velocidad varía de manera uniforme. Esto significa que el módulo de velocidad aumenta o disminuye a valores iguales en intervalos de tiempo iguales.

Entendiendo el Movimiento Acelerado, Retardado y Uniforme

El movimiento de una partícula se dice que es variado cuando su velocidad escalar instantánea varía en el transcurso del tiempo. Si, en cierto intervalo de tiempo, la partícula se mueve cada vez más rápido, es decir, si el módulo de su velocidad escalar instantánea está siempre en aumento (creciente), su movimiento variado será del tipo acelerado. Así, el movimiento de un automóvil, cuyo velocímetro proporciona las indicaciones ilustradas en la figura siguiente, es acelerado.

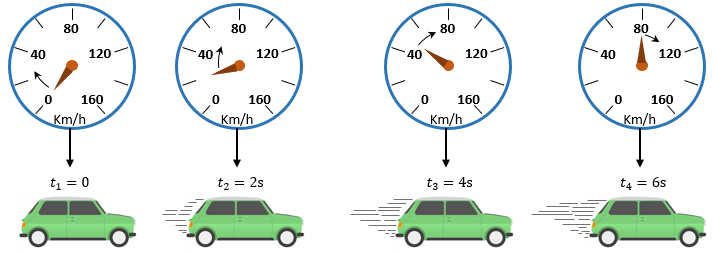
Si una partícula se mueve cada vez más lentamente durante cierto intervalo de tiempo, es decir, si el módulo de su velocidad escalar instantánea es siempre decreciente, su movimiento variado será del tipo retardado. Es el caso del movimiento de un automóvil cuyo velocímetro proporciona los valores presentes en la figura siguiente.

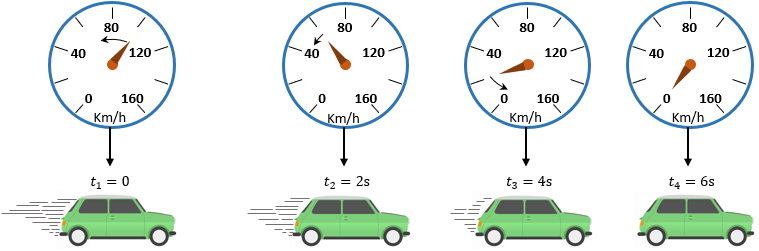
Ahora por otro lado, si consideramos, sin embargo, el movimiento en que la indicación del velocímetro es siempre la misma durante cierto intervalo de tiempo, no tendremos un movimiento variado, sino uniforme. Es el caso del movimiento de un automóvil cuyo velocímetro proporciona, en todo momento, un valor constante, como el indicado en la figura siguiente.

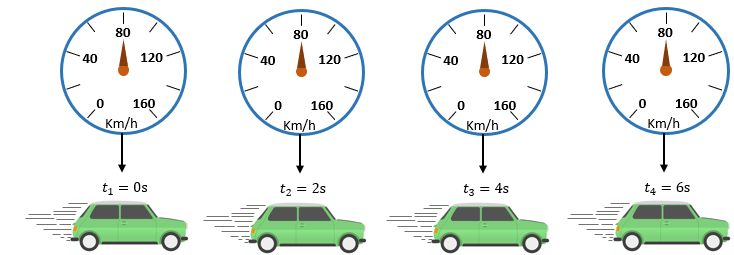
Antes de terminar las comparaciones del movimiento, observe que, en el movimiento uniforme, la aceleración escalar es constante e igual a cero, sin importar el valor de la velocidad escalar.

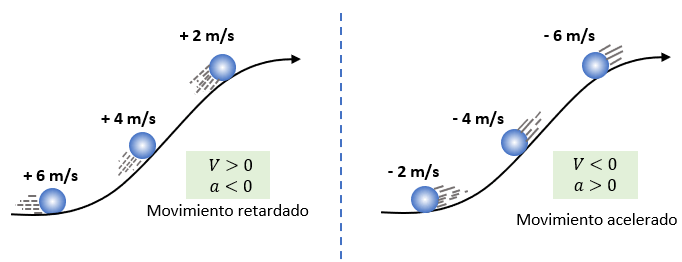
En un movimiento acelerado, la velocidad escalar y la aceleración escalar tienen el mismo signo, es decir, son ambas positivas o ambas negativas, como muestran los ejemplos siguientes.

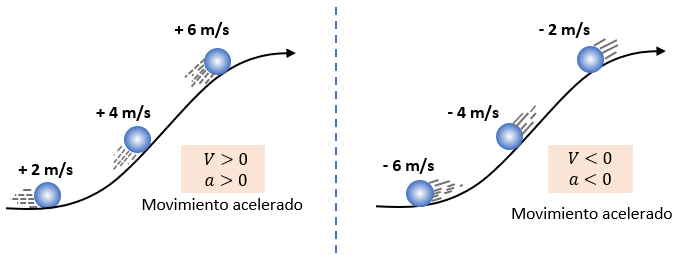
Por otro lado también existe el caso siguiente:

En un movimiento retardado, la velocidad escalar y la aceleración escalar tienen signos contrarios.

🤔 ¿Aceleración Negativa o Desaceleración?

Como ya dijimos en relación a la velocidad, en Física el adjetivo negativo está casi siempre relacionado al sentido de referencia, y no a la reducción o disminución del módulo de una magnitud. La aceleración negativa, por ejemplo, no siempre reduce el módulo de la velocidad del móvil, si la velocidad también es negativa, su módulo aumentará. Por esa razón, no vamos a utilizar, en este artículo el término desaceleración como sinónimo de aceleración negativa, pues desacelerar, según el Diccionario es "reducir la velocidad, velocidad lenta".

📐 Fórmula de la Aceleración

Como hemos visto hasta ahora, la aceleración es la expresión de la variación de la velocidad respecto al tiempo, y la podemos expresar matemáticamente de la siguiente manera:

$\displaystyle a=\frac{v-{{v}_{0}}}{t-{{t}_{0}}}$

De esa misma fórmula, podemos despejar a la velocidad en términos de la aceleración y tiempo, quedando así:

$\displaystyle v={{v}_{0}}+a(t-{{t}_{0}})$

En caso de que el tiempo inicial (t0) fuera igual a 0, entonces la fórmula quedaría de la siguiente manera:

$\displaystyle v={{v}_{0}}+at$

📓 Ejercicios Resueltos de MRUA

Solución:

a) El movimiento que describe la partícula es sin duda un movimiento rectilíneo uniformemente acelerado, puesto que la trayectoria es rectilínea y la aceleración es constante.

b) Para poder calcular la aceleración, debemos aplicar la fórmula que mencionamos anteriormente, de tal forma que la aceleración nos da:

$\displaystyle a=\frac{v-{{v}_{0}}}{t-{{t}_{0}}}=\frac{25-5}{10-0}=\frac{20}{10}=2\frac{m}{{{s}^{2}}}$

Nuestra aceleración es de 2 metros por segundo cuadrado.

c) Nos piden calcular la función de la velocidad en relación al tiempo, simplemente sustituimos en la fórmula.

$\displaystyle v={{v}_{0}}+at$

$\displaystyle v=5+2t$

¡¡Muy fácil!!.

d) Para saber que velocidad tendrá la partícula en el instante de t = 8s, basta con sustituir el valor de "t" en la fórmula anterior.

$\displaystyle v=5+2(8)=5+16=21\frac{m}{s}$

Por lo que la velocidad en el instante t = 8s, es de 21 m/s²

e) En este caso nos piden determinar en que instante de tiempo la partícula tendrá una velocidad de 15 m/s, volvemos a sustituir este valor en la fórmula, simplemente despejando a la variable "t" es decir:

$\displaystyle v={{v}_{0}}+at$

Despejando a "t"

$\displaystyle t=\frac{v-{{v}_{0}}}{a}$

Sustituyendo el valor de la velocidad

$\displaystyle t=\frac{v-{{v}_{0}}}{a}=\frac{15-5}{2}=\frac{10}{2}=5s$

Es decir que cuando la partícula tenga una velocidad de 15 m/s, ocurrirá justamente a los 5 segundos.

Más fórmulas en el Movimiento Rectilíneo Uniformemente Acelerado

En este artículo nos evitaremos las demostraciones para llegar a las fórmulas, ya en otra ocasión hablaremos de como obtenerlas. Por ahora pensemos en las diversas fórmulas que nos encontramos en este tema, por ejemplo:

$\displaystyle d={{v}_{0}}t+\frac{a{{t}^{2}}}{2}$

$\displaystyle d=\frac{{{v}_{f}}^{2}-{{v}_{0}}^{2}}{2a}$

$\displaystyle d=\frac{{{v}_{f}}-{{v}_{0}}}{2}t$

El emplear cualquiera de las tres fórmulas anteriores nos dan el mismo resultado, solo se usan dependiendo los datos que tengamos en el problema.

Las mimas fórmulas anteriores se pueden simplificar todavía más si es que el objeto o partícula parte del reposo, pues v0 = 0, entonces:

$\displaystyle d=\frac{a{{t}^{2}}}{2}$

$\displaystyle d=\frac{{{v}_{f}}^{2}}{2a}$

$\displaystyle d=\frac{{{v}_{f}}}{2}t$

$\displaystyle vf={{v}_{0}}+at$

$\displaystyle v{{f}^{2}}={{v}_{0}}^{2}+2ad$

Al igual que las fórmulas anteriores, si en dado caso que el móvil o partícula parta del reposo, entonces su velocidad inicial será 0, es decir que las fórmulas se simplificarían de la siguiente forma:

$\displaystyle {{v}_{f}}=at$

$\displaystyle {{v}_{f}}^{2}=2ad$

Más ejemplos resueltos de Movimiento Rectilíneo Uniformemente Acelerado

Solución: 

Usaremos las fórmulas de distancia, sin embargo el problema nos advierte que el automóvil parte del reposo, eso es importante porque sabemos que la velocidad inicial será cero, es decir:

$\displaystyle {{v}_{0}}=0$

Ahora, los datos que tenemos son:

$\displaystyle a=3.5\frac{m}{{{s}^{2}}}$

$\displaystyle t=7s$

Aplicaremos la siguiente fórmula:

Sustituyendo nuestros datos:

$\displaystyle d=\frac{a{{t}^{2}}}{2}=\frac{(3.5){{(7)}^{2}}}{2}=\frac{171.5}{2}=85.75m$

Por lo que nuestro automóvil habrá recorrido 85.75 metros después de los 7 segundos.

Solución:

a) Para calcular la aceleración media, basta con aplicar la fórmula de la aceleración explicada más arriba. De tal forma que tendremos:

$\displaystyle a=\frac{{{v}_{f}}-{{v}_{0}}}{t}=\frac{9\frac{m}{s}-5\frac{m}{s}}{4s}=1\frac{m}{{{s}^{2}}}$

Ahora pasemos a calcular la distancia recorrida, recordar que aquí si existe una velocidad inicial, por lo que debemos de tener cuidado al elegir nuestra fórmula.

b) Aplicando la fórmula correcta:

$\displaystyle d={{v}_{0}}t+\frac{a{{t}^{2}}}{2}$

Sustituyendo nuestros datos en la fórmula:

$\displaystyle d={{v}_{0}}t+\frac{a{{t}^{2}}}{2}=\left( 5\frac{m}{s} \right)\left( 4s \right)+\frac{\left( 1\frac{m}{{{s}^{2}}} \right){{\left( 4s \right)}^{2}}}{2}=20m+\frac{16m}{2}=28m$

Por lo que tendremos 28 metros recorridos 😀

a) Si la motocicleta parte del reposo, entonces tenemos una velocidad inicial igual a cero (V0 = 0), con esto podemos elegir una fórmula que no contenga a la velocidad inicial, ahora también sabemos que lo que nos pide es el tiempo que le toma transcurrir una determinada velocidad, por lo qué la fórmula que usaremos será:

Despejando a "t"

$\displaystyle t=\sqrt{\frac{2d}{a}}$

La distancia está en Kilómetros, primero necesitamos pasar esta distancia en metros, por lo que tendremos que realizar nuestra conversión:

$\displaystyle 1.6km\left( \frac{1000m}{1km} \right)=1600m$

1.6 km = 1600 m

Sustituyendo nuestros datos en la fórmula:

$\displaystyle t=\sqrt{\frac{2d}{a}}=\sqrt{\frac{2(1600m)}{0.45\frac{m}{{{s}^{2}}}}}=84.32s$

Por lo que a la motocicleta le tomará 84.32 segundos recorrer 1600 metros.

b) Como nos piden obtener la rapidez en el tiempo que le tomó los 1600 metros, vamos a utilizar la siguiente fórmula.

$\displaystyle {{v}_{f}}=at$

Sustituyendo nuestros datos

$\displaystyle {{v}_{f}}=at=\left( 0.45\frac{m}{{{s}^{2}}} \right)\left( 84.32s \right)=37.94\frac{m}{s}$

Para poder expresar el resultado final de la velocidad, en términos de km/h, solamente aplicaríamos los factores de conversión.

$\displaystyle {{v}_{f}}=37.94\frac{m}{s}\left( \frac{1km}{1000m} \right)\left( \frac{3600s}{1h} \right)=136.58\frac{km}{h}$