Movimiento Rectilíneo Uniforme - Ejercicios Resueltos

Dentro del estudio del movimiento en Física, y teniendo en cuenta los principios de la velocidad media e instantánea, podemos empezar a investigar más a fondo sobre estos temas de cinemática, tal como los movimientos rectilíneos uniformes, en especial sobre el MRU (Movimiento Rectilíneo Uniforme).

Bien, cuando una partícula se mueve con velocidad constante, en relación a un determinado sistema de referencia, su movimiento es rectilíneo uniforme (MRU). En el MRU no tiene diferencia entre velocidad media e instantánea, no existe aceleración y la única magnitud que varía con el tiempo es la posición. Así, el estudio del movimiento rectilíneo uniforme se resume al estudio de la variación de la posición de ese punto respecto al tiempo.

Función de la posición respecto al tiempo

Para establecer la función de la posición en relación al tiempo de alguna partícula en MRU es necesario, inicialmente, establecer el sistema de referencia adecuado.

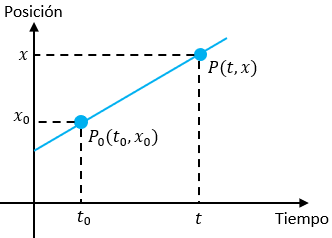
Vea la siguiente figura.

En este sistema de referencia se establece el origen 0 y la posición inicial x0 , que ha sido medida en el instante t0 a partir de ese origen. Se representan también la velocidad media y la posición x del punto final en el instante t.

Siendo constante, el módulo de la velocidad, la posición de la partícula es igual al módulo de su velocidad (vm) en cualquier intervalo de tiempo, es decir:

Así pues, en definición de la velocidad media, podemos escribir:

Esta es la función de la posición en relación al tiempo del MRU. Permite obtener la posición x (variable dependiente) de la partícula para cada instante t (variable independiente). Los términos v, x0 y t0 son constantes. En general, es posible admitir que el tiempo inicial sea igual a cero t0 = 0; solo basta suponer que el inicio del cronometraje del movimiento esté desde la posición inicial en cero y, en este caso, la función se vuelve más simple.

Estudio de las gráficas de MRU

El estudio de un movimiento puede ser hecho tanto con la ayuda de las funciones que lo describen, como por medio de los gráficas correspondientes. Las funciones permiten un tratamiento matemático más simplificado, en cuanto a las gráficas permiten la mejor visualización de la forma en que varían las magnitudes que describen el movimiento. En este post veremos las diversas gráficas y como podemos solucionar problemas de éste tipo.

Gráfica de Posición vs Tiempo (x vs t)

La función de la posición de un MRU es lineal es decir de primer grado por lo que su gráfico es una recta. Observe el gráfico siguiente:

De esta gráfica podemos calcular la pendiente, dicha pendiente tiene por fórmula:

Si esta fórmula se aplica en los dos puntos que tenemos en nuestra gráfica de arriba, obtendremos.

Por lo qué podemos concluir que la media es igual a la velocidad en esos puntos.

Tomar en cuenta el siguiente punto.

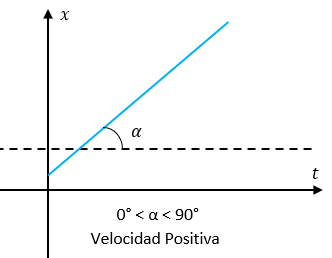
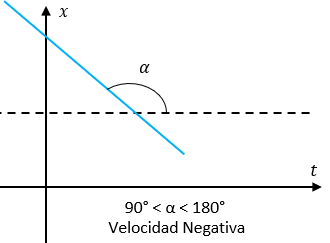
Cuando la partícula se desplaza en el sentido positivo del eje, el módulo de su velocidad es precedido de la señal positiva por lo que el coeficiente angular de la recta, representado por la inclinación α, está comprendido en el intervalo 0<α<90° , ahora, por otro lado, cuando la partícula se desplaza en el sentido contrario, la inclinación está comprendida en el intervalo 90°<α<180 °. En este caso, el módulo de velocidad es precedido de la señal negativa.

Veamos los gráficos.

a) Velocidad Positiva

b) Velocidad Negativa

Ahora veamos otro tipos de gráfica.

Gráfica de Velocidad vs Tiempo

Como en el MRU la velocidad es constante, la función de la velocidad en relación al tiempo también es constante. Por lo tanto el gráfico de velocidad x tiempo es una recta paralela al eje del tiempo. Esta recta estará por encima del eje si la velocidad es positiva o por debajo del eje si es negativa, como en las siguientes gráficas:

a) Velocidad positiva, por encima del eje del tiempo.

b) Velocidad negativa, por debajo del eje del tiempo.

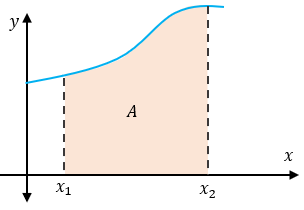
Se puede demostrar que el desplazamiento en el intervalo de tiempo Δt, representado en el gráfico abajo por Δx, es igual al "área bajo la curva" del gráfico velocidad x tiempo en ese mismo intervalo de tiempo. Es decir:

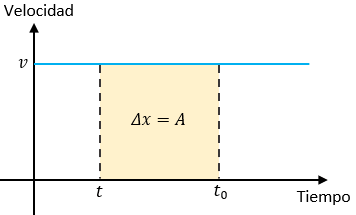
Se llama "área bajo la curva" la región comprendida entre la curva de la función y el eje de las abscisas. En la figura siguiente, el "área bajo la curva", A, en amarillo, está comprendida entre la curva y las coordenadas x1 y x2 del eje de las abscisas.

Esta área se calcula de la misma forma que el área de la figura plana correspondiente, pero tiene un significado diferente, por lo que siempre nos referimos a ella entre comillas. Así, el "área bajo la curva" del gráfico velocidad x tiempo del MRU es el área de un rectángulo, pero no tiene la dimensión de superficie. La dimensión del "área bajo la curva" es igual a la dimensión del producto de las dimensiones de las magnitudes representadas en los ejes cartesianos. En el gráfico velocidad x tiempo, es igual a la dimensión de velocidad (longitud: tiempo) multiplicada por la dimensión del tiempo, resultando en la dimensión de longitud, pues:

Ejercicios Resueltos de MRU con gráficas

Para entender mucho mejor los conceptos de gráficas y la representación de las velocidades, es bueno partir con ejercicios resueltos, así que aquí vamos.

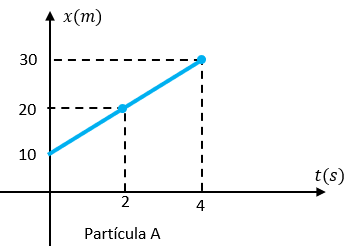
A) Solución para la partícula A

Recordemos que lo que nos pide el problema, es encontrar la velocidad de la partícula A, para ello veamos las posiciones iniciales que tiene dicha partícula. En la gráfica podemos observar que su posición inicial es a 10 metros, en el tiempo de 0 segundos, posteriormente avanza 20 metros a los 2 segundos, y finalmente sigue su trayectoria hasta los 30 metros a los 4 segundos. Como podemos observar, vamos a considerar las posiciones iniciales y finales.

t0 = 0 segundos

t = 2 segundos

x0 = 10 metros

x = 20 metros

es decir:

Ahora aplicando nuestra fórmula de velocidad

Lo que vendría a ser la velocidad de la partícula A.

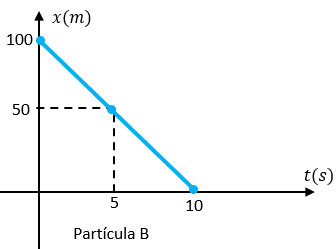
B) Solución para la partícula B

Al analizar la gráfica para la partícula B, podemos ver que la posición a los 0 segundos es de 100 metros, después de los 5 segundos la posición ahora está a los 50 metros y finalmente a los 10 segundos la posición es de 0 metros, ¿cómo calculamos la velocidad?, de la misma forma que el paso anterior.

t0 = 0 segundos

t = 5 segundos

x0 = 100 metros

x = 50 metros

es decir:

Aplicando la fórmula de velocidad:

Para poder encontrar una función de posición con respecto al movimiento de la partícula, debemos de considerar que el tiempo inicial siempre será cero, y que a partir de ahí podamos calcular lo que queramos con la partícula, entonces nuestra fórmula quedaría:

Ahora despejando a "x"

a) Encontrando la función para la partícula A

Simplemente vamos a sustituir en la fórmula los datos que tenemos del problema, y en el "tiempo" no vamos a colocar ningún tiempo, solamente el valor de "t".

De otra forma:

¿Sencillo?, muy fácil 😀

b) Encontrando la función para la partícula B

Con esto podemos calcular la posición de la partícula en cualquier instante de tiempo "t". Solamente sustituyendo el segundo por el valor en ese instante.

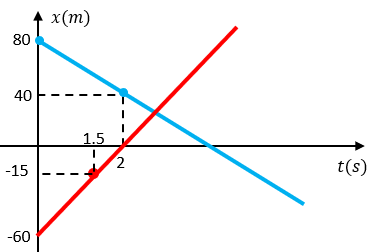
Solución: 

Con ver la gráfica, podemos empezar a realizar nuestros cálculos sin ningún problema, por ejemplo podríamos decir que la trayectoria del auto azul es (A) y la trayectoria del auto rojo es (B), para entendernos mejor, ahora empecemos por calcular lo que nos pide el problema.

A) Calculando la posición del automóvil azul 

El auto azul tiene una posición de 80 metros a los 0 segundos, y después a los 2 segundos, tiene una posición de 40 metros, con estos datos podemos decir entonces que:

Basándonos en la fórmula:

Nos encontramos con que la velocidad del auto azul es de -20 m/s, o sea que va en reversa.

Ahora es momento de encontrar su función de posición.

Sustituyendo datos:

Ahora vamos con el otro automóvil.

B) Calculando la posición del automóvil rojo

El auto rojo tiene una posición de -60 metros a los 0 segundos, y de -15 metros a los 1.5 segundos, con estos datos podemos decir que:

De la fórmula podemos decir que:

Para encontrar su función de posición, la podemos hacer sustituyendo los valores que tenemos en la fórmula:

Quedando así:

C) Obteniendo el instante donde se encuentran ambos automóviles

Para poder obtener el instante donde se encuentra ambos automóviles, basta con igualar sus ecuaciones de posición, quedando así:

Agrupamos a "t"

Simplificamos

Despejamos a "t"

Esto quiere decir que a los 2.8 segundos se van a encontrar ambos automóviles, pero si quisiéramos saber ¿a qué distancia?, basta con sustituir ese valor de "t" en cualquiera de las dos funciones de posición de ambos autos.

i) Comprobando posición en automóvil azul

Entonces sustituimos el tiempo "2.8 segundos" en la función de posición de este auto.

A los 24 metros se encontrarán ambos autos.

ii) Comprobando posición en automóvil rojo

Veamos si el cálculo es correcto para ambos:

Como era de esperarse, a los 24 metros con 2.8 segundos ambos automóviles se encontrarán 😎

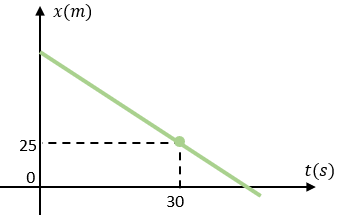
Solución: 

Observando el gráfico, nos damos cuenta que tenemos un punto de partida, que son los 25 metros recorridos  a los 30 segundos, sin embargo desde nuestra gráfica también observamos que el niño en bicicleta va de reversa, es decir, está volviendo desde su punto de partida, por lo que la velocidad debe considerarse negativa. Si tiene dudas, por favor lea el comienzo de este artículo. Asumiendo esta parte, podemos decir que:

Nota: No confundir la "x" de posición con la "x" del eje de las abscisas, por ahora "x" para nosotros es la posición final que deseamos encontrar.

Aplicando la fórmula con la que hemos venido trabajando, decimos que:

Reducimos la expresión

Despejando a "x"

Multiplicando por (-1) e invirtiendo la igualdad

Listo!!! 😀

Con esto podemos darnos cuenta que el niño en bicicleta a los 18 segundos estará a 55 metros.