Velocidad Media e Instantánea - Ejercicios Resueltos

Antes de empezar a estudiar el Movimiento Rectilíneo Uniforme (MRU) o el Movimiento Rectilíneo Uniformemente Acelerado (MRUA) debemos comprender los conceptos básicos del movimiento, y resolver ejercicios para entender el contexto de la cinemática en Física. 😀

¿Qué es el movimiento en Física?

La idea de movimiento, en el lenguaje cotidiano, tiene significado amplio y casi siempre ligado a la vida, es difícil imaginar la vida sin movimiento; a menudo la vida es sinónimo de movimiento. Sin embargo, en Física, la palabra movimiento, como todas las palabras, adquiere un significado más preciso: el movimiento es siempre un concepto relativo; sólo tiene sentido hablar en movimiento de un cuerpo en relación a otro cuerpo. Por ejemplo: un pasajero sentado en un autobús que recorre una carretera está en movimiento en relación a un árbol junto al camino, pero está parado en relación con el autobús.

La idea de "parado" o "en movimiento" tiene en cuenta el cambio, o no, de la ubicación del cuerpo en relación a otro que sirva de referencia respecto al tiempo. En otras palabras, un cuerpo está en movimiento cuando su posición, en relación a determinado cuerpo de referencia, varía con el paso del tiempo. (Estamos utilizando la expresión cuerpo de referencia en lugar de sistemas de referencia o referencial porque, como veremos más adelante, cuerpos como poste, carro, árbol no pueden ser considerados sistema de referencia o referenciales. Esta es una definición inicial, provisional, que permite algunas conclusiones interesantes.

En el choque de un coche contra un poste, por ejemplo, se puede afirmar que el coche golpeó el poste si el poste es el cuerpo de referencia, o que el poste golpeó en el coche si el coche es el cuerpo de referencia. Esta última afirmación puede parecer absurda porque estamos acostumbrados a relacionar todas las cosas con la tierra o el suelo. Y, en relación al suelo, por supuesto que el poste está fijo y el coche está en movimiento. Pero si una mosca está posada en la ventana del coche durante la colisión, seguramente verá el poste avanzando contra el coche y hacía si mismo ¿se entiende?. El concepto de movimiento requiere de un análisis muy estudiado.

Espacio Recorrido y Velocidad Escalar

La definición de movimiento permite pensar inicialmente en dos conceptos genéricos y provisionales, pero que nos son muy útiles en el día a día, sin embargo se estudia en Física.

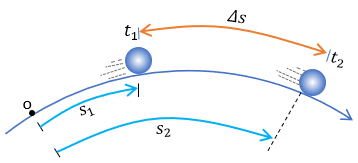
Espacio Recorrido

El primero de ellos es el concepto de espacio recorrido, definido como la medida de la longitud del recorrido del cuerpo en movimiento. Esta medida suele ser obtenida entre dos referencias, como los marcos kilométricos de una carretera. Vea la imagen de abajo. El espacio recorrido es la longitud del camino recorrido por el móvil para ir de A a B, cuanto más curvas hace, mayor el espacio recorrido, aunque la longitud del segmento de recta que une los puntos inicial y final del recorrido no se altere.

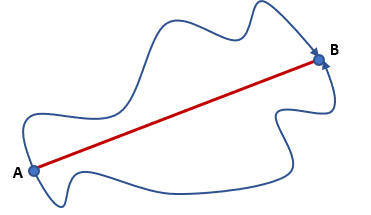
El segundo concepto es el de velocidad escalar, que da la idea cuantitativa o numérica de la rapidez con que el cuerpo se mueve.

Velocidad Escalar

La palabra velocidad tiene diversos significados, uno de ellos es la rapidez, que no pueden ser confundido con el concepto físico de velocidad. El concepto de velocidad escalar que aparece aquí debe entenderse como provisional; ya el concepto físico de velocidad será presentado en el artículo de Movimiento Rectilíneo Uniforme (MRU). La principal diferencia entre ellos es que la velocidad es un vector, tiene módulo, dirección y sentido, mientras que la velocidad escalar es una magnitud escalar, tiene sólo valor numérico y unidad. En otras palabras, dos automóviles que se cruzan en diferentes calles de una avenida con velocidad de 40 km/h no tienen la misma velocidad, en el sentido que la Física da al término, porque tienen sentidos diferentes.

La velocidad escalar puede estar relacionada con un intervalo de tiempo, cuando se llama velocidad media, o velocidad instantánea o promedio.

La velocidad escalar media de un cuerpo es, por definición, la razón entre el espacio recorrido (Δs) y el intervalo de tiempo (Δt) tiempo necesario para recorrerlo. Matemáticamente lo podemos expresar de la siguiente manera:

$\displaystyle {{V}_{m}}=\frac{\Delta s}{\Delta t}$

El intervalo de tiempo Δt puede expresarse mediante la diferencia entre el instante inicial t0 y el instante final t, correspondientes al inicio y al final del recorrido considerado Así, el intervalo de tiempo está representado por la expresión:

$\displaystyle \Delta t=t-{{t}_{0}}$

La unidad de la velocidad escalar media o instantánea se obtiene por la razón entre las unidades de espacio recorrido (longitud) y de tiempo. Como en el SI (Sistema Internacional) la unidad de longitud es el metro (m) y la de tiempo es el segundo (s), la unidad de velocidad es el metro por segundo (m / s).

Velocidad Instantánea

Aunque comúnmente se pueden confundir los términos de velocidad media con velocidad instantánea, la diferencia entre ambas radica en una medida de aproximación, por ejemplo, si estamos calculando la velocidad en intervalos de tiempos muy pequeños, tan pequeños que se aproximan a cero, es cuando decimos que dicho movimiento ocurrirá en un instante. Matemáticamente esto podemos expresarlo de la siguiente manera:

$\displaystyle {{v}_{\acute{i}nst}}=\underset{\Delta t\to 0}{\mathop{\lim }}\,\frac{\Delta s}{\Delta t}$

Si no tienes conocimientos de cálculo diferencial, no te preocupes. No hay nada difícil en la fórmula anterior. Solamente estamos diciendo que cuando queremos calcular la velocidad instantánea en un punto de la velocidad media, tenemos que hacer que el tiempo se acerque a cero, para saber la velocidad en ese instante, o sea pedazos de segundos cada vez más pequeños. Por lógica, si la velocidad se mantiene siempre constante, entonces diremos que tanto la velocidad media como la velocidad instantánea serán las mismas, o sea iguales.

Ejercicios Resueltos de Velocidad Media

Solución: 

Sabemos que la distancia recorrida fue de 420 kilómetros, es decir, Δs =420 km, pero también sabemos que el tiempo inicial (t0) fue a las 10 horas, y que el tiempo final al destino (t) fue a las 17 horas, entonces procedemos al cálculo.

$\displaystyle {{V}_{m}}=\frac{\Delta s}{\Delta t}=\frac{420km}{17h-10h}=\frac{420km}{7h}=60\frac{km}{h}$

Por lo que la velocidad media del automóvil fue de 60 km/hr

Solución:

En este caso nos proporcionan la velocidad media, y los tiempos tanto de salida como de llegada. Lo único que necesitamos es el espacio recorrido, pero como bien sabemos, lo podemos despejar de nuestra fórmula.

$\displaystyle {{V}_{m}}=\frac{\Delta s}{\Delta t}$

Despejando a "Δs"

$\displaystyle \Delta s=\left( {{V}_{m}} \right)\left( \Delta t \right)$

Debemos tener mucho cuidado con la hora de aterrizaje, ya que las 11 horas con 30 minutos, está expresado también en minutos, debemos pasar los minutos a horas; haciendo una simple conversión de unidades.

$\displaystyle 30\min \left( \frac{1h}{60\min } \right)=0.5h$

Ahora sabemos que 11 con 30 minutos es igual a 11.5 horas; con esta conversión ya podemos seguir resolviendo el problema.

$\displaystyle \Delta s=\left( 910\frac{km}{h} \right)\left( 11.5h-7h \right)=\left( 910\frac{km}{h} \right)\left( 4.5h \right)=4095km$

Solución:

Basándonos en los datos del problema, donde nos proporciona el tiempo hasta oír el rayo, y la velocidad con que éste se propaga, entonces necesitamos nuestra fórmula de "espacio" en términos de la velocidad y tiempo, usando la fórmula:

Entonces, sustituyendo:

$\displaystyle \Delta s=\left( 330\frac{m}{s} \right)\left( 3s \right)=990m$

Lo que vendría a ser 990 metros de distancia, desde donde posiblemente se haya impactado el trueno.

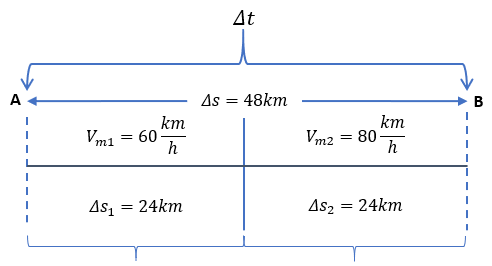
Solución:

Aunque en principio el problema puede ser difícil, no lo es. El problema es claro, nos pide encontrar la velocidad total, sabiendo que la motocicleta recorrió dos distancias con velocidades medias diferentes, entonces tenemos un problema dentro de dos problemas más sencillos. En primera, para el problema general necesitamos resolver el tiempo que le tomó a la motocicleta recorrer los dos tramos a velocidades medias distintas.

Para encontrar Δt necesitamos:

$\displaystyle \Delta t=\Delta {{t}_{1}}+\Delta {{t}_{2}}$

Obteniendo Δt1

$\displaystyle \Delta {{t}_{1}}=\frac{\Delta {{s}_{1}}}{\Delta {{V}_{{{m}_{1}}}}}=\frac{24km}{60\frac{km}{h}}=0.4h$

Obtenemos 0.4 horas

Obteniendo Δt2

$\displaystyle \Delta {{t}_{2}}=\frac{\Delta {{s}_{2}}}{\Delta {{V}_{{{m}_{2}}}}}=\frac{24km}{80\frac{km}{h}}=0.3h$

Obtenemos 0.3 horas

Con estos datos, ya podemos obtener la velocidad media total del problema inicial. Hacemos entonces:

$\displaystyle \Delta {{V}_{m}}=\frac{\Delta s}{\Delta {{t}_{1}}+\Delta {{t}_{2}}}=\frac{48km}{0.4h+0.3h}=\frac{48km}{0.7h}=68.57\frac{km}{h}\approx 69\frac{km}{h}$